Cours complet pour apprendre les différents types de bases de données et le langage SQL

• L'algèbre relationnelle fournit les opérateurs de base pour manipuler les extensions des relations (ensembles de n-uplets ou tables) d'une BD relationnelle.
• On peut faire un parallèle avec l'arithmétique qui fournit les opérations de base pour manipuler les nombres (addition, soustraction, multiplication et division).
• Tout SGBD relationnel se doit de fournir des implantations efficaces de ces opérateurs.
• Une requête SQL est traduite, comme on le verra, en un arbre d'opérateurs de l'algèbre relationnelle.

L'algèbre relationnelle permet de construire des expressions à partir :

• de noms de relations :

  • relations stockées dans la BD,
  • relations temporaires ;
• de comparateurs, de connecteurs logiques, d'opérateurs arithmétiques... ;

• d'opérateurs ensemblistes qui :

  • sélectionnent certaines parties d'une relation,
  • combinent les n-uplets de deux relations.

Une expression de l'algèbre relationnelle a pour valeur une relation :

• elle exprime une requête à la BD dont la réponse est la valeur de cette expression.

On notera :

• p, q, r des expressions de l'algèbre relationnelle ;
• A, B, C des noms d'attributs ;
• schéma(r) le schéma de la relation valeur de l'expression r ;
• ext(r) l'extension de la relation valeur de l'expression r ;
• t.A la valeur de l'attribut A dans le n-uplet t.

• conc la concaténation de deux n-uplets :

  • (v₁, …, v_m) conc (w₁, …, w_n) = (v₁, …, v_m, w₁, …, w_n).

Si R est le nom d'une relation, alors R est une expression telle que :

• schéma(R) = schéma de la relation désignée par R ;
• extension(R) = extension de la relation désignée par R.

Il est possible de créer des relations temporaires.

L'instruction :

• R := e

crée une relation temporaire de nom R dont le schéma et l'extension sont celles de la relation valeur de l'expression e.

Les principaux opérateurs de l'algèbre relationnelle sont les suivants :

• renommage ;
• union, intersection et différence ;
• produit cartésien ;
• sélection ;
• projection ;

• jointure :

  • interne,
  • externe,
  • naturelle ;
• division.

VI-D-1. Renommage▲

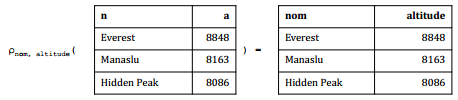
L'opérateur de renommage (ρ) permet de renommer les attributs d'une relation.

Soit r une expression telle que :

• schéma(r) = (A₁, …, A_n)

l'opérateur ρ est défini par :

• kitxmlcodeinlinelatexdvpsch\acute{e}ma\left(\rho _{B_1, \dots, B_n}(r)\right) = (B_1, \dots, B_n)finkitxmlcodeinlinelatexdvp
• kitxmlcodeinlinelatexdvpext\left(\rho _{B_1, \dots, B_n}(r)\right) = ext(r)finkitxmlcodeinlinelatexdvp

VI-D-2. Union, intersection et différence▲

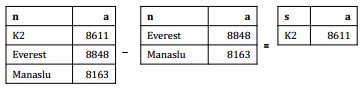
Soit p et q deux expressions telles que :

• schéma(p) = schéma(q) = (A₁: D₁, …, A_n: D_n)

Les opérateurs d'union (∪), d'intersection (⋂) et de différence (—) sont définis par :

• schéma(p ∪ q) = (A₁: D₁, …, A_n: D_n)
• ext(p ∪ q) = {t | t ∈ ext(p) ∨ t ∈ ext(q)}
• schéma(p ⋂ q) = (A₁: D₁, …, A_n: D_n)
• ext(p ⋂ q) = {t | t ∈ ext(p) ∧ t ∈ ext(q)}
• schéma(p — q) = (A₁: D₁, …, A_n: D_n)
• ext(p — q) = {t | t ∈ ext(p) ∧ t ∉ ext(q)}

VI-D-3. Produit cartésien▲

Soit p et q deux expressions telles que :

• schéma(p) = (A₁, …, A_m)
• schéma(q) = (B₁, …, B_n)
• {A₁, …, A_m} ⋂ {B₁, …, B_n} = Ø

Le produit cartésien (×) est défini par :

• schéma(p × q) = (A₁, …, A_m, B₁, …, B_n)
• ext(p × q) = {u conc v | u ∈ ext(p) ∧ v ∈ ext(q)}

VI-D-4. Sélection▲

L'opérateur de sélection (σ) extrait l'ensemble des n-uplets d'une relation qui vérifient une condition donnée.

Une condition est une expression booléenne (c'est-à-dire dont la valeur est vraie ou fausse) :

• dont les opérandes sont soit des valeurs de domaine, soit des noms d'attributs de la relation à laquelle s'applique la sélection ;
• les opérateurs sont les comparateurs : <, <=, =, >=, >, != et les connecteurs logiques : ∧, ∨, ¬.

Par exemple :

• altitude > 8500 ∧ (face = "S" ∨ face = "SO") est une condition applicable aux n-uplets de la relation sommet.

Soit r une expression telle que :

• schéma(r) = (A₁, …, A_n).

L'opérateur σ est défini par :

• schéma(σ_cond) = (A₁, …, A_n) ;
• ext(σ_cond) = {t | t ∈ ext(r) ∧ val(cond)}.

VI-D-5. Projection▲

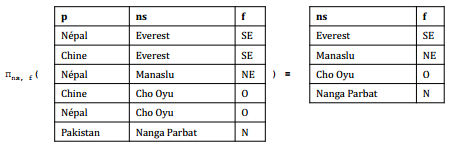
L'opérateur de projection (π) extrait l'ensemble des valeurs d'un constituant d'une relation.

Soit r une expression telle que :

• schéma(r) = (A₁: D₁, …, A_n: D_n)

L'opérateur de projection est défini par :

• schéma(πA₁, …, A_n(r)) = (A₁: D₁, …, A_n: D_n) ;
• ext(πA₁, …, A_n(r)) = {(t.A₁, …, t. A_n) | t ∈ ext(r)}.

VI-D-6. Jointure▲

La jointure est l'opération qui permet de concaténer des n-uplets provenant de deux tables et vérifiant une certaine condition.

On distingue trois types de jointure :

• la jointure interne ;
• la jointure externe ;
• la jointure naturelle.

La jointure n'est pas un opérateur primitif :

• Elle peut être réalisée, selon son type, en combinant les opérateurs de produit cartésien, de sélection, de projection et de renommage.

VI-D-6-a. Jointure interne▲

L'opérateur de jointure interne (join) fusionne deux relations en produisant toutes les concaténations possibles de leurs n-uplets respectifs qui vérifient une certaine condition.

La jointure interne est équivalente à un produit cartésien suivi d'une sélection :

• p join_cond q ≡ σ_cond(p × q)

VI-D-6-b. Jointure externe▲

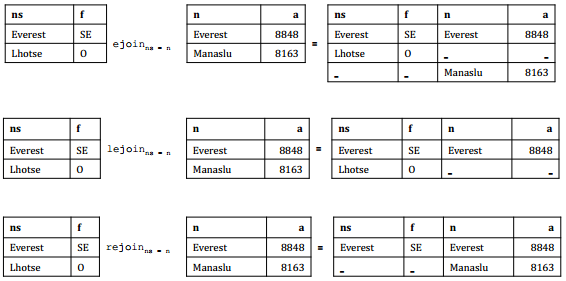
L'opérateur de jointure externe permet d'ajouter au résultat d'une jointure interne les n-uplets de l'une, de l'autre ou des deux relations qui ne peuvent pas être joints.

Soit P et Q les relations à joindre, on distingue :

• la jointure externe totale (ejoin) qui ajoute les n-uplets de P et de Q qui ne peuvent pas être joints ;
• la jointure externe gauche (lejoin) qui n'ajoute que les n-uplets de P qui ne se joignent pas avec un n-uplet de Q ;
• la jointure externe droite (rejoin) qui n'ajoute que les n-uplets de Q qui ne se joignent pas avec un n-uplet de P.

Les n-uplets ainsi rajoutés sont complétés par des valeurs nulles pour les attributs qu'ils ne possèdent pas.

Soit p et q deux expressions telles que :

• schéma(p) = (A₁, …, A_m) ;
• schéma(q) = (B₁, …, B_n) ;
• {A₁, …, A_m} ⋂ { B₁, …, B_n} = Ø.

L'opérateur ejoin est défini par :

• schéma(p ejoin_cond q) = (A₁, …, A_m, B₁, …, B_n) ;
• ext(p ejoin_cond q) = p_ext ∪ j ∪ q_ext.

où :

VI-D-6-c. Jointure naturelle▲

Dans une jointure, qu'elle soit interne ou externe, on peut omettre la condition lorsqu'elle se restreint à ce que les attributs de même nom de chacune des relations à joindre doivent avoir la même valeur :

• on appelle jointure naturelle ce cas particulier de jointure.

La jointure naturelle sera notée en omettant la condition sous l'opérateur de jointure considéré.

Dans la relation produite, les attributs communs aux deux relations n'apparaîtront qu'une seule fois.

Si les deux relations à joindre n'ont pas d'attributs communs, alors la jointure naturelle est équivalente au produit cartésien.

Soit p et q deux expressions telles que :

• schéma(p) = (A₁, …, A_m) ;
• schéma(q) = (B₁, …, B_n) ;
• {A₁, …, A_m} ⋂ { B₁, …, B_n} = {C₁, …, C_k}.

La jointure naturelle est définie par :

• schéma(p j q) = (A₁, …, A_m, L)
• kitxmlcodeinlinelatexdvpp\ j\ q\ =\ \pi_{A_1,\ \dots,\ A_m,\ L} (p\ join_{C_1\ =\ C_1\ \wedge\ \dots\ \wedge\ C_k\ =\ C'_k}\ q') finkitxmlcodeinlinelatexdvp

où :

• j est l'un des opérateurs join, ejoin, lejoin, rejoin ;
• L est la liste des attributs de q dans laquelle les attributs C₁, …, C_k ont été supprimés ;
• q' est la relation obtenue à partir de q en renommant respectivement C'₁, …, C'_k les attributs C₁, …, C_k avec
  {A₁, …, A_m, B₁, …, B_n} ⋂ {C'₁, …, C'_k} = Ø

Nom et altitude des sommets de plus de 8000 m dont la 1^re ascension a été réalisée par la face nord ?

• réponse := π_{nom, altitude}(σ_{face = "N"}(sommet));

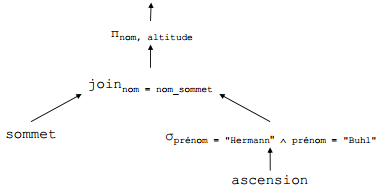
Nom et altitude des sommets de plus de 8000 m dont la 1^re ascension a été réalisée par Hermann Buhl ?

• ahb := σ_{prénom = "Hermann" ∧ nom = "Buhl"}(ascension)
• réponse := π_{nom, altitude}(sommet join_{nom = nom_sommet} ahb)

Nom des sommets de plus de 8000 m dont l'altitude est supérieure à celle du Makalu ?

• am := ρ_{altitude_makalu}(π_altitude(σ_{nom = "Makalu"}(sommet)));
• réponse := π_nom(sommet join_{altitude > altitude_makalu} am);

Prénom et nom des grimpeurs ayant réalisé la 1^re ascension d'un sommet de plus de 8000 m du Népal ?

• asn := ascension join σ_{pays = "Népal"}(localisation);
• réponse := π_{prénom_grimpeur, nom_grimpeur}(asn);

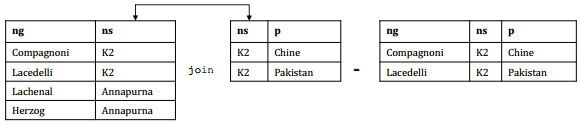
Nom des sommets de plus de 8000 m qui ne sont pas au Népal (on sélectionne les noms des sommets qui ne joignent pas avec les sommets du Népal) ?

• nsn := π_{nom_sommet}(σ_{pays = "Népal"}(localisation))
• réponse := π_nom(σ_{nom_sommet = nul}(sommet ejoin_{nom = nom_sommet} nsn));

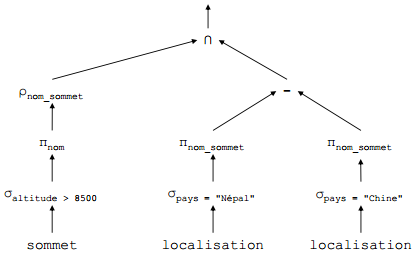
Nom des sommets de plus de 8500 mètres situés au Népal mais pas sur la frontière chinoise ?

• ns := ρ_{nom_sommet}(π_nom(σ_{altitude > 8500}(sommet)));
• nsn := π_{nom_sommet}(σ_{pays = "Népal"}(localisation));
• nsc := π_{nom_sommet}(σ_{pays = "Chine"}(localisation));
• réponse := ns ∩ nsn ∩ nsc;

Une requête de l'algèbre relationnelle peut être représentée par un arbre, appelé arbre de requête, dont les nœuds sont des opérateurs et les arcs des extensions de relations.

On considérera un nom de relation comme l'opérateur qui produit l'extension de la relation ayant ce nom.