VIII. Normalisation▲
VIII-A. Le problème▲
Mélanger dans une même relation des informations relatives à plusieurs entités entraîne, en général des redondances d'information qui provoquent les anomalies suivantes :
- anomalies d'insertion ;
- anomalies de mise à jour ;
- anomalies de suppression.
VIII-B. Exemple▲
|
isbn |
titre |
éditeur |
pays |
|---|---|---|---|
|
2-212-09283-0 |
Bases de données - objet et relationnel |
Eyrolles |
France |
|
2-7117-8645-5 |
Fondements des bases de données |
Vuibert |
USA |
|
0-201-70872-8 |
Databases and Transaction Processing |
Addison Wesley |
USA |
|
2-212-09069-2 |
Internet/Intranet et bases de données |
Eyrolles |
France |
Cette relation qui décrit des livres et leurs éditeurs, contient des redondances provoquant les anomalies suivantes :
- Insertion : il n'est pas possible d'insérer un livre sans connaître son éditeur. Attribuer une valeur nulle aux attributs éditeur et pays violerait l'intégrité d'entité : un attribut appartenant à la clé, ne doit pas avoir de valeur nulle.
- Mise à jour : si un éditeur change de pays, il faut modifier ce pays pour chacun des livres qu'il a édités.
- Suppression : si l'unique livre publié par un éditeur est supprimé, l'information sur cet éditeur est perdue. Attribuer une valeur nulle aux attributs isbn et titre violerait l'intégrité d'entité.
VIII-C. Solution▲
La solution à ces problèmes consiste à normaliser la relation en cause en la décomposant en plusieurs relations.
Cette décomposition s'appuie sur les dépendances qui existent entre les attributs de la relation initiale :
- dépendances fonctionnelles ;
- dépendances multivaluées.
Par exemple, la dépendance entre l'ISBN d'un livre et son titre ou bien entre le nom d'un éditeur et son pays.
VIII-D. Dépendances fonctionnelles▲
Il y a une dépendance fonctionnelle entre un constituant X et un constituant Y d'une relation R si pour toute extension de R, à chaque valeur de X il correspond toujours la même valeur de Y.
On dit que X détermine fonctionnellement Y et l'on note :
- X → Y
Un constituant {A1, …, An} apparaissant à gauche ou à droite du signe → sera noté A1 … An.
VIII-D-1. Dépendances fonctionnelles triviales▲
Une dépendance fonctionnelle X → Y est dite triviale si Y est un sous-ensemble de X ou bien si Y est vide.
Par exemple, les dépendances :
- isbn titre → pitre
- éditeur pays → Ø
sont triviales.
VIII-D-2. Propriétés des dépendances fonctionnelles▲
À partir d'un ensemble de dépendances fonctionnelles, on peut en déduire d'autres.
Par exemple, à partir des dépendances :
- éditeur → ville
- ville → pays
on peut déduire, par transitivité, la dépendance :
- éditeur → pays
Étant donné un ensemble de dépendances fonctionnelles F construit sur l'ensemble R des attributs d'une relation, l'ensemble F+ (fermeture de F) de toutes les dépendances fonctionnelles logiquement impliquées par F peut être calculé à partir des trois règles suivantes (axiomes d'Armstrong) :
- (réflexivité) si Y ⊆ X ⊆ R alors X → Y
- (augmentation) si X → Y et Z ⊆ R alors X ∪ Z → Y ∪ Z
- (transitivité) si X → Y et Y → Z alors X → Z
Des axiomes d'Armstrong, on peut déduire deux règles plus pratiques pour calculer F+ :
- (union) si X → Y et X → Z alors X → Y ∪ Z.
- (décomposition) si X → Y ∪ Z alors X → Y et X → Z.
VIII-D-3. Dépendances fonctionnelles et clés▲
On peut définir une clé d'une relation comme un sous-ensemble de ses attributs qui détermine tous les autres.
Un constituant X d'une relation R(A1, …, An) est une clé de cette relation si et seulement si :
- X → A1, …, An,
- il n'existe pas de constituant Y inclus dans X tel que Y → A1, …, An.
Étant données une relation et l'une de ses clés, on appelle :
- attribut clé un attribut qui appartient à cette clé ;
- attribut non clé un attribut qui ne lui appartient pas.
On appelle super-clé un constituant qui inclut une clé.
Par exemple dans la relation :
- personne(nom, prénom, age)
de clé {nom, prénom} :
- nom et prénom sont des attributs clés ;
- age est un attribut non clé ;
- {nom, prénom, age} est une super-clé.
VIII-D-4. Normalisation d'une relation▲
La normalisation d'une relation consiste à la décomposer en un ensemble de relations telles qu'aucune des relations obtenues ne possède les anomalies de redondance, de mise à jour et de suppression.
Relativement aux dépendances fonctionnelles, on distingue quatre formes normales :
- la 1re forme normale ;
- la 2e forme normale ;
- la 3e forme normale ;
- la forme normale de Boyce-Codd qui est la plus aboutie.
Ce sont les deux dernières que l'on cherche à atteindre :
- la 1re est impliquée par l'atomicité des valeurs ;
- la 2e n'est qu'une étape vers la 3e.
VIII-D-4-a. Propriétés d'une décomposition▲
Soit R une relation et R1, …, Rn les relations issues d'une décomposition D de R :
- D est sans perte si la relation R peut être recomposée par jointures des relations R1, …, Rn.
- D préserve les dépendances fonctionnelles si les dépendances fonctionnelles de R sont impliquées par les dépendances fonctionnelles de R1, …, Rn.
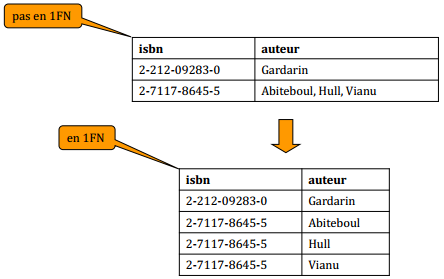
VIII-D-4-b. 1re forme normale▲
Une relation est en 1re forme normale si tous ses attributs ont une valeur atomique.
Le fait que, dans le modèle relationnel, les domaines soient atomiques implique que toutes les relations sont en 1re forme normale.
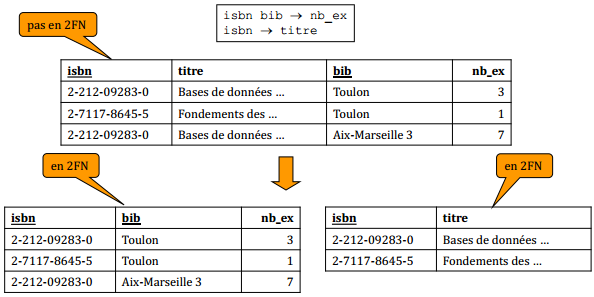
VIII-D-4-c. 2e forme normale▲
Une relation est en 2e forme normale si elle est en 1re forme normale et si chaque attribut non-clé dépend totalement et non partiellement de la clé primaire.
Cette décomposition est sans perte et préserve les dépendances fonctionnelles.
VIII-D-4-c-i. Insuffisance de la 2e forme normale▲

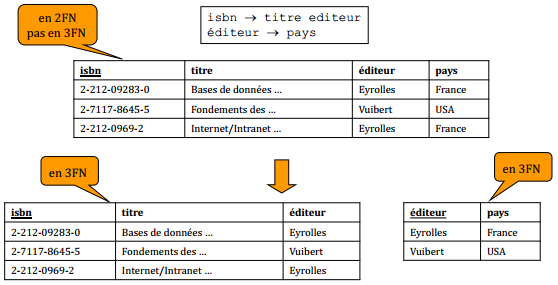
Il reste des redondances : (…, Eyrolles, France).
VIII-D-4-d. 3e forme normale▲
Une relation est en 3e forme normale si pour chaque dépendance fonctionnelle non triviale X → Y, on a :
- soit, X est une super-clé de R ;
- soit, Y appartient à une clé candidate de R.
La 2e partie de la règle est importante, car elle dit qu'un constituant d'une clé candidate peut dépendre :
- soit d'un constituant d'une clé candidate ;
- soit d'un constituant non-clé ;
ce qui peut être source de redondances.
Cette décomposition est sans perte et préserve les dépendances fonctionnelles.
Cette décomposition est sans perte et préserve les dépendances fonctionnelles.
VIII-D-4-d-i. Insuffisance de la 3e forme normale▲
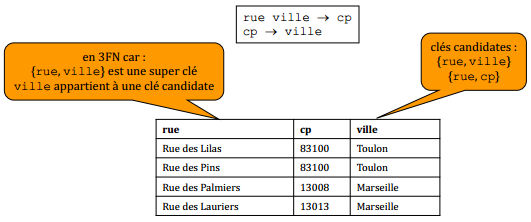
Il reste des redondances : (…, 83100, Toulon).
VIII-D-4-e. Forme normale de Boyce-Codd▲
Une relation R est en forme normale de Boyce-Codd (FNBC) si, pour chaque dépendance fonctionnelle non triviale X → Y, X est une super-clé de R.
La forme normale de Boyce-Codd implique la 3e forme normale.
La forme normale de Boyce-Codd est la forme idéale relativement aux dépendances fonctionnelles, mais malheureusement elle peut ne pas préserver les dépendances fonctionnelles.
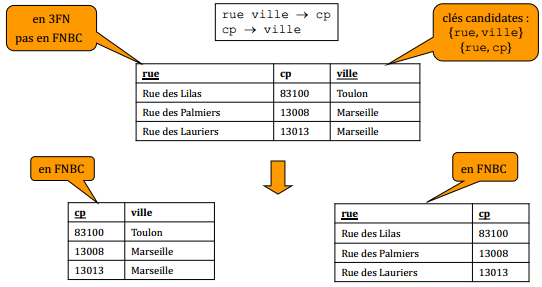
Cette décomposition est sans perte, mais ne préserve pas les dépendances fonctionnelles.
VIII-D-4-f. Décomposition en 3e forme normale et en FNBC▲
Il est démontré que :
- toute relation a au moins une décomposition en 3e forme normale qui préserve les dépendances fonctionnelles et qui est sans perte ;
- toute relation a au moins une décomposition en forme normale de Boyce-Codd qui est sans perte, mais qui peut ne pas préserver les dépendances fonctionnelles.
VIII-E. Dépendances multivaluées▲
Il y a une dépendance multivaluée entre un constituant X et un constituant Y d'une relation R(X, Y, Z) si, pour toute extension de R, à chaque valeur de X il correspond toujours le même ensemble de valeurs de Y et que cet ensemble de valeurs ne dépend pas des valeurs de Z.
On dit que X multidétermine Y et l'on note :
- X →→ Y
Soit par exemple la relation :
- livre(isbn, titre, auteur)
Si un livre peut avoir plusieurs auteurs, la relation livre possède la dépendance multivaluée :
- isbn →→ auteur
Soit un livre d'isbn i et d'auteurs a1, a2 et a3. Si le triplet (i, t, a1) apparaît dans une extension de la relation livre, alors les triplets (i, t, a2) et (i, t, a3) doivent y apparaître aussi.
VIII-E-1. 4e forme normale▲
Une dépendance multivaluée X →→ Y d'une relation R est dite non triviale si :
- Y n'est pas un sous-ensemble de X ;
- X ∪ Y n'inclut pas tous les attributs de R.
Une relation R est en 4e forme normale, si pour chaque dépendance multivaluée X →→ Y non triviale, X est une super-clé de R.
La 4e forme normale implique la forme normale de Boyce-Codd puisqu'une dépendance fonctionnelle est un cas particulier de dépendance multivaluée.
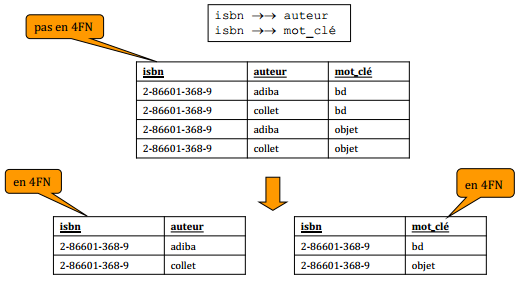
Cette décomposition est sans perte et préserve les dépendances fonctionnelles.
VIII-E-2. Décomposition en 4e forme normale ▲
Il est démontré que toute relation a au moins une décomposition en 4e forme normale qui est sans perte, mais qui peut ne pas préserver les dépendances fonctionnelles.
Soit U la relation à décomposer et D l'ensemble des dépendances existantes entre les attributs de U :
- S := {U}
-
Tant qu'il existe dans S une relation R qui n'est pas en 4e forme normale :
- on cherche dans D une dépendance X →→ Y telle que R(X, Y, Z) et X n'est pas une clé de R,
- on ajoute à Y l'ensemble Z' des attributs de Z fonctionnellement déterminés par X, produisant la dépendance X →→ Y Z',
- on remplace R dans S par les deux relations R1(X, Y ∪ Z') et R2(X, Z - Z').
S = {U(isbn, titre, auteur, mot_clé, éditeur, pays, bib, nb_ex)}
D = {isbn → titre,
isbn → éditeur,
éditeur → pays,
isbn →→ auteur, isbn →→ mot_clé,
isbn bib → nb_ex}
S = {U1(isbn, titre, éditeur, pays),
U2(isbn, auteur, mot_clé, bib, nb_ex)}
S = {U1(isbn, titre, éditeur, pays),
U21(isbn, auteur),
U22(isbn, mot_clé, bib, nb_ex)}
S = {U1(isbn, titre, éditeur, pays),
U21(isbn, auteur),
U221(isbn, mot_clé),
U222(isbn, bib, nb_ex)}
S = {U11(éditeur, pays),
U12(isbn, titre, éditeur),
U21(isbn, auteur),
U221(isbn, mot_clé),
U222(isbn, bib, nb_ex)}
Les relations de S sont en 4e forme normale (et donc en forme normale de Boyce-Codd) et les dépendances sont préservées.
VIII-F. Bilan▲
|
3FN |
FNBC |
4FN |
|
|---|---|---|---|
|
Élimination de la redondance due aux dépendances fonctionnelles |
Pas toutes |
Oui |
Oui |
|
Élimination de la redondance due aux dépendances multivaluées |
Non |
Non |
Oui |
|
Préservation des dépendances fonctionnelles |
Oui |
Pas toujours |
Pas toujours |
|
Préservation des dépendances multivaluées |
Pas toujours |
Pas toujours |
Pas toujours |