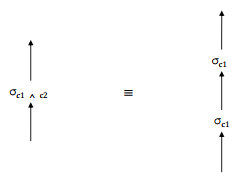X. Résolution des requêtes▲
X-A. Introduction ▲
L'accès à une BD relationnelle est réalisé au travers d'un langage de requêtes (SQL, le plus souvent). Les performances de l'évaluateur de requêtes sont donc cruciales.
Un langage de requêtes est déclaratif : l'utilisateur exprime sa requête, mais pas la façon d'y répondre.
Or, pour une requête donnée, il existe en général plusieurs stratégies pour construire la réponse. C'est au SGBD de choisir la stratégie optimale.
X-B. Les 3 phases de la résolution d'une requête▲
La résolution d'une requête à une BD relationnelle se déroule en trois phases :
- Traduction de la requête en un arbre d'opérateurs relationnels (sélection, jointure, projection, etc.) : l'arbre de requête.
-
Optimisation. Il s'agit de déterminer un plan d'exécution de coût minimal. Deux procédures sont principalement mises en œuvre :
- transformation de l'arbre de requête en un arbre équivalent, basée sur les propriétés d'associativité et de commutativité de l'algèbre relationnelle,
- évaluation du coût de résolution de chaque opérateur.
- Évaluation du plan d'exécution produit par la phase 2.
X-C. Arbre de requête▲
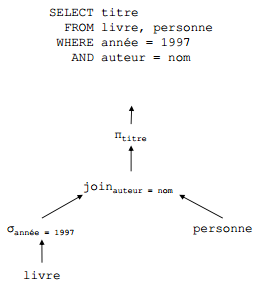
X-D. Évaluation des opérateurs relationnels▲
Nous étudierons quelques méthodes d'évaluation des opérateurs :
- de sélection ;
- de jointure ;
- de projection.
X-D-1. Méthodes d'évaluation d'une sélection▲
Simple boucle (parcours séquentiel)
Indexée
- utilisation d'un index primaire pour retrouver un n-uplet dont la clé est donnée ou appartient à un intervalle donné ;
- utilisation d'un index secondaire pour retrouver un ensemble de n-uplets dont la clé est donnée ou appartient à un intervalle donné.
X-D-2. Méthodes d'évaluation d'une jointure▲
Sur une condition quelconque :
- boucles imbriquées
Equi-jointure :
-
pas d'index sur les constituants de jointure :
- boucles imbriquées
- tri-fusion
- hachage
-
index sur l'un des constituants de jointure :
- indexée
-
index triés sur les deux constituants de la jointure :
- fusion des feuilles des deux index
X-D-3. Méthodes d'évaluation d'une projection▲
Simple boucle
Tri puis simple boucle, si les doubles doivent être éliminés.
X-E. Étude de quelques méthodes▲
On supposera que chaque relation est stockée dans un fichier qui contient les n-uplets de cette relation.
Le coût d'une opération sera mesuré en nombre de transferts de pages entre disque et mémoire centrale.
Ce coût peut se décomposer en deux parties :
- un coût de production de la relation résultat ;
- un coût d'écriture de cette relation.
Le coût de production dépend de la méthode choisie pour réaliser l'opération alors que le coût d'écriture en est indépendant.
Dans le cas d'une évaluation pipeline d'une suite d'opérations :
- op1, ..., opn
les résultats des opérations op1, ..., opn-1 ne sont pas stockés sur disque, car les n-uplets produits sont directement transmis à l'opérateur suivant :
- les coûts de lecture d'une relation opérande ou d'écriture des résultats d'un opérateur peuvent donc être nuls.
X-E-1. Coût de production d'une opération▲
Le coût de production de la relation résultat dépend :
- de la méthode utilisée pour résoudre l'opération ;
- des paramètres d'implantation des relations opérandes.
Le jeu de paramètres utilisé sera le suivant :
|
card(R) |
cardinalité de la relation R |
|
nb(R) |
nombre de blocs occupés par le fichier R |
|
nbatt(R) |
nombre d'attributs de la relation R |
|
nv(R, X) |
nombre de valeurs différentes du constituant X de la relation R |
X-E-2. Coût d'écriture du résultat▲
Le coût d'écriture de la relation résultat est indépendant de la méthode de résolution utilisée.
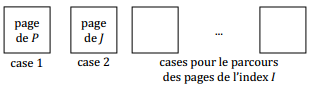
Cette écriture est réalisée au travers du tampon de la façon suivante :
- Une case C du tampon est affectée à la relation résultat initialisée avec une page vide P.
-
Pour chaque n-uplet t produit :
- Si la page P est pleine, l'écrire sur un bloc du disque.
- Placer une nouvelle page vide P dans la case C.
- Écrire t dans P.
Le coût d'écriture du résultat est donc égal à nb(relation résultat).
X-F. Sélection par simple boucle▲
|
S:= σcond(R) |
|
|
|
Algorithme |
|
Pour chaque bloc du fichier R faire |
|
Coût de production |
X-G. Sélection indexée▲
X-H. Comparaison des deux méthodes▲
Soit une relation livre telle que :
- card(livre) = 12000
- nb(livre) = 2400
- nv(livre, année) = 50
- Il existe un index I sur l'attribut année
Le coût de production de l'opération :
- σannée = 2000(livre)
est égal à :
-
sélection par boucle :
- 2400
-
sélection indexée :
- ⌈2400/50⌉ = 48, si l'index est groupant,
- min(⌈12000/50⌉, 2400) = 240, si l'index est non groupant.
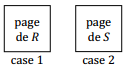
X-I. Jointure par boucles imbriquées▲
|
J := P joincond Q |
|
|
|
Algorithme |
|
pour chaque suite de M blocs de P faire |
Coût de production
kitxmlcodelatexdvpnb(P) + \left\lceil \frac{nb(P)}{M} \right\rceil \times nb(Q)finkitxmlcodelatexdvpSi nb(P) ≤ M, c.-à-d. si la relation P tient en mémoire, le coût est égal à :
kitxmlcodelatexdvpnb(P) + nb(Q)finkitxmlcodelatexdvpLe coût est minimum si l'on choisit la relation de cardinalité minimum comme relation externe.
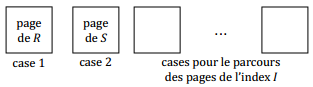
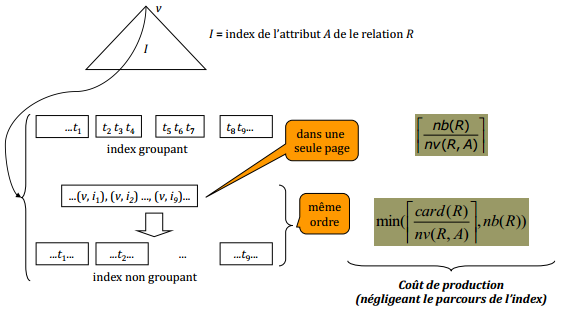
X-J. Jointure indexée▲
|
J := P joinA = B Q |
|
A est un attribut de |
|
|
|
Algorithme |
|
pour chaque bloc de P faire |
|
Coût de production |
|
kitxmlcodeinlinelatexdvpnb(P) + card(P) \times \left\lceil \frac{nb(Q)}{nv(Q,B)} \right\rceilfinkitxmlcodeinlinelatexdvp Si l'index I est groupant |
|
kitxmlcodeinlinelatexdvpnb(P) + card(P) \times min\left( \left\lceil \frac{card(Q)}{nv(Q,B)} \right\rceil, nb(Q)\right )finkitxmlcodeinlinelatexdvp Si l'index I est non groupant |
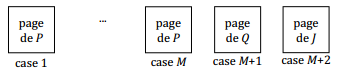
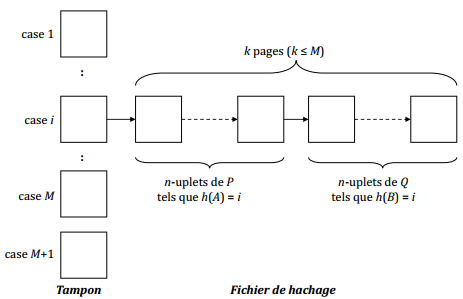
X-K. Équi-jointure par hachage▲
|
J := P joinA = B Q |
|
A est un attribut de P |
|
|
|
Algorithme |
|
pour chaque bloc de P faire |
|
Condition |
|
Il faut que le nombre de pages liées à une case du répertoire soit ≤ M pour qu'elles tiennent dans le tampon. |
|
kitxmlcodeinlinelatexdvpnb(P) + nb(Q) \le M^2finkitxmlcodeinlinelatexdvp |
|
Coût de production |
X-L. Comparaison des trois méthodes▲
Soit une relation livre(ISBN, nom_auteur) telle que :
- card(livre) = 24000, nb(livre) = 2400 ;
- nv(livre, nom_auteur) = 6000 ;
- il existe un index I non groupé sur l'attribut nom_auteur.
et une relation auteur(nom, pays) telle que :
- card(auteur) = 6000, nb(auteur) = 600
- nv(auteur, nom) = 6000
102 cases sont disponibles dans le tampon.
Le coût de production de l'opération :
- auteur joinnom = nom_auteur livre
est égal à :
-
jointure par boucles imbriquées :
- 600 + ⌈600 / 100⌉ × 2400 = 15000
-
jointure indexée :
- 600 + 6000 × min(⌈24000 / 6000⌉, 2400) = 24600
-
jointure par hachage :
- 3 × (2400 + 600) = 9000 qui est donc, dans ce cas, la meilleure solution.
X-M. Projection sans élimination des doublons▲
|
P := πA1, ..., Ak(R) |
|
Coût de production |
X-N. Évaluation de la taille de la relation résultat▲
La taille de la relation produite par un opérateur est mesurée en nombre de n-uplets et en nombre de blocs.
Cette évaluation n'est pas toujours simple. Elle nécessite de disposer de connaissances statistiques sur les données.
Nous ne traitons ici que les cas les plus simples.
On suppose que :
- les valeurs d'un attribut sont réparties uniformément sur les n-uplets d'une relation ;
- tous les attributs d'une même relation ont la même taille.
X-N-1. Taille du résultat d'une sélection▲
X-N-2. Taille du résultat d'une jointure▲
Dans le cas où nv(P, A) ≤ nv(Q, B), on peut faire l'hypothèse que chaque n-uplet de P se joint avec au moins un n-uplet de Q et inversement.
kitxmlcodelatexdvpcard(P\ join_{A=B}(Q)) = \left\lceil \frac{card(P) \times card(Q)}{\max(nv(P,A), nv(Q,B))} \right\rceilfinkitxmlcodelatexdvp kitxmlcodelatexdvpnb(P\ join_{A=B}(Q)) = \left\lceil \frac{card(P) \times nb(Q) + card(Q)\times nb(P)}{\max(nv(P,A), nv(Q,B))} \right\rceilfinkitxmlcodelatexdvpX-N-3. Taille du résultat d'une projection ▲
On suppose que les valeurs des attributs d'une relation ont la même taille (ce qui est très approximatif).
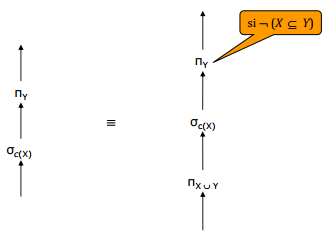
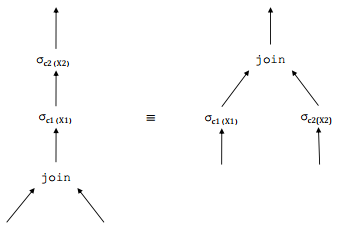
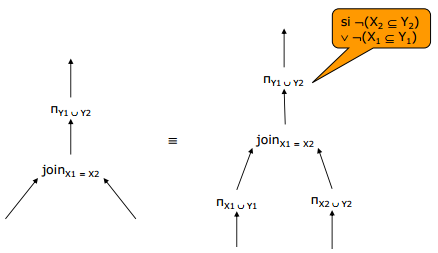
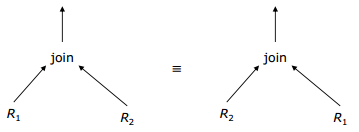
kitxmlcodelatexdvpcard(\pi_{A1, \dots, Ak}(R)) = card(R)finkitxmlcodelatexdvp kitxmlcodelatexdvpnb(\pi_{A1, \dots, Ak}(R)) = \left\lceil \frac{k}{nbatt(R)} \times nb(R) \right\rceilfinkitxmlcodelatexdvpX-O. Propriétés des opérateurs relationnels▲
|
|
|
|
|
|
|
|
|
|
|
|
X-P. Choix d'un plan d'exécution▲
En théorie, le choix d'un plan d'exécution peut être effectué de la façon suivante :
- Traduire la requête sous forme d'un arbre de requête initial : dans le cas où la requête est un bloc SELECT … FROM … WHERE …, l'arbre de requête initial est obtenu en réalisant la jointure ou le produit cartésien des relations impliquées (clause FROM), suivi d'une sélection (clause WHERE), suivie d'une projection (clause SELECT).
- Construire l'ensemble des arbres équivalents à l'arbre initial en appliquant les propriétés de commutativité et d'associativité des opérateurs.
- À partir de chacun de ces arbres, générer tous les plans d'exécution possibles en associant à chaque opérateur chacune des méthodes de résolution applicable.
- Évaluer le coût de chaque plan d'exécution.
- Choisir le plan de coût minimal.
L'inconvénient majeur de cette méthode est que le nombre de plans d'exécution à examiner croît très vite avec le nombre de relations sur lesquelles porte la requête.
Par exemple, on peut montrer que le nombre d'ordres de jointures de n relations est :
- (2 × (n — 1)) ! / (n — 1) !
Ce nombre croît donc très vite quand n augmente. Il est égal à 12 pour n = 3, 1680 pour n = 5, 665280 pour n = 7...
En pratique, on utilise des règles heuristiques pour diminuer le nombre de plans d'exécution à évaluer.
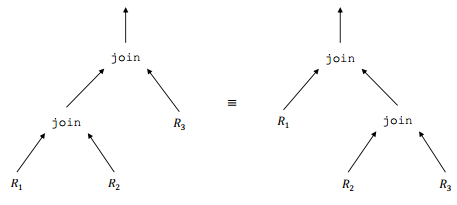
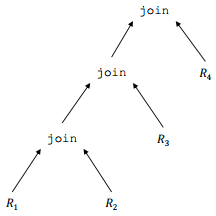
X-Q. Arbres linéaires de jointure▲
|
|
X-R. Étude de cas▲
Schéma :
- livre(isbn, titre, auteurs, nom_éditeur, année, prix)
- éditeur(nom, adresse, pays)
Requête :
- Titres des livres publiés en 2000 édités par un éditeur espagnol ?
2.
3.
4.
5.
SELECT titre
FROM livre, editeur
WHERE nom = nom_editeur
AND pays = 'Espagne'
AND année = 2000;
X-S. Paramètres▲
Tables
|
nbatt |
card |
nb |
nv(titre) |
nv(nom_éditeur) |
nv(année) |
|
|---|---|---|---|---|---|---|
|
livre |
6 |
12000 |
2400 |
12000 |
300 |
20 |
|
nbatt |
card |
nb |
nv(nom) |
nv(pays) |
|
|---|---|---|---|---|---|
|
éditeur |
3 |
300 |
60 |
300 |
30 |
Index ; Tampon 52 cases
|
index groupant ? |
|
|---|---|
|
livre(isbn) |
oui |
|
livre(nom_éditeur) |
non |
|
livre(année) |
non |
|
éditeur(nom) |
oui |
|
éditeur(pays) |
non |
X-T. Arbre de requêtes initial▲
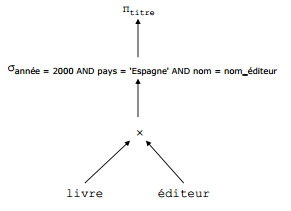
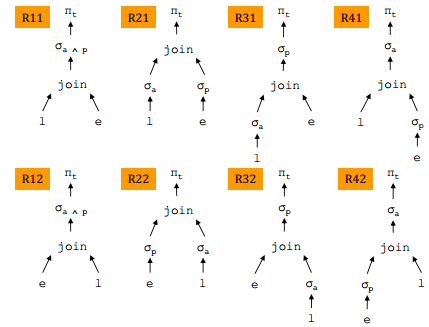
X-U. Arbres de requêtes équivalents▲
Par application des règles T1, T3 et T5 à l'arbre initial R11
l = livre
e = éditeur
a = année = 2000
p = pays = 'Espagne'
X-V. Étude de 4 plans d'exécution▲
On évalue les plans d'exécution correspondant aux arbres de requête R12, R22, R32 et R42.
Ces plans consistent à réaliser la jointure en choisissant comme relation externe la relation éditeur qui est beaucoup moins volumineuse que la relation livre et à traiter les relations en pipeline chaque fois que c'est possible.
L'étiquette (c, b) de chaque arête indique la cardinalité et le nombre de blocs pour la relation associée à cette arête.
Une arête en trait épais indique que la relation est traitée en pipeline.
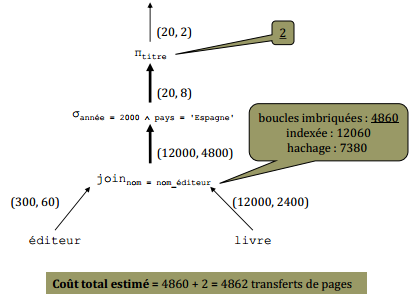
X-V-1. Plan n° 1 (arbre de requête R12)▲
|
|
|
Coût total estimé = 4860 + 2 = 4862 transferts de pages |
X-V-2. Plan n° 2 (arbre de requête R22)▲
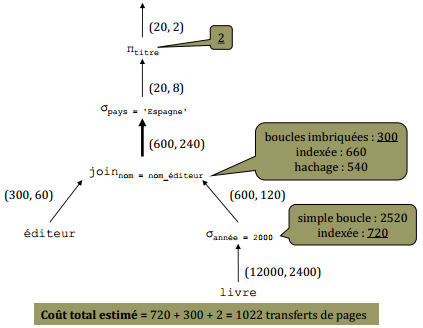
X-V-3. Plan n° 3 (arbre de requête R32)▲
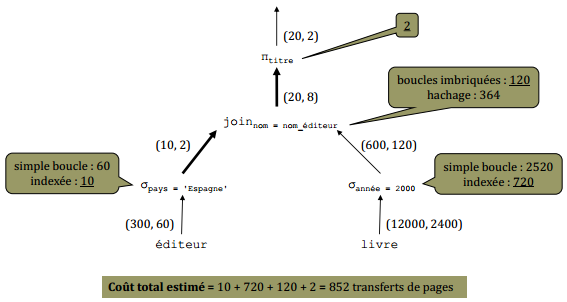
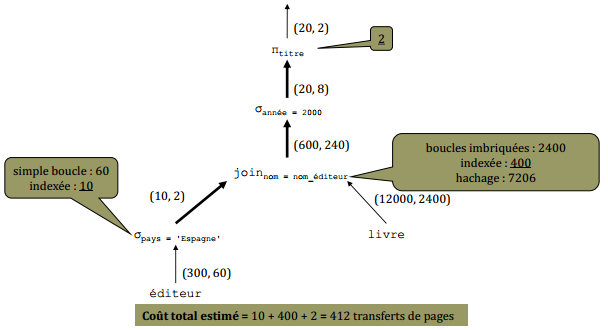
X-V-4. Plan n° 4 (arbre de requête R42)▲
X-V-5. Choix du meilleur plan▲
The winner is : le plan n° 4 !