Cours complet pour apprendre les systèmes de gestion de bases de données

L'interface nouvelle offerte par un SGBD déductif est avant tout le langage de règles.

Le langage de règle est donc utilisé afin de spécifier les parties conditions et actions des règles de déduction. Plus précisément, à partir des prédicats B1, B2… Bn définis dans la base implantée (extensionnelle), le langage de règles permet de spécifier comment construire des prédicats dérivés R1, R2… interrogeables par les utilisateurs. Un langage de règles peut donc être perçu comme une extension des langages de définition de vues et de triggers des SGBD relationnels classiques.

L'extension est de taille, car le langage de définition et de manipulation de connaissances va intégrer les fonctionnalités suivantes :

1. La possibilité d'effectuer les opérations classiques du calcul relationnel (union, restriction, projection, jointure, différence) ;
2. Le support des ensembles incluant les fonctions d'agrégats traditionnelles des langages relationnels classiques ainsi que les attributs multivalués ;
3. La récursivité, qui permet de définir une relation déduite en fonction d'elle-même ;
4. La négation, qui permet de référencer des faits non existants dans la base ;
5. Les fonctions arithmétiques et plus généralement celles définies par les utilisateurs ;
6. Les mises à jour des faits au travers des règles ;
7. La modularité avec la gestion de niveaux d'abstraction successifs et de métarègles.

En bref, toutes les facilités qui existent dans les langages de développement de bases de données vont chercher à figurer dans les langages de règles. L'objectif est d'ailleurs de remplacer ces langages.

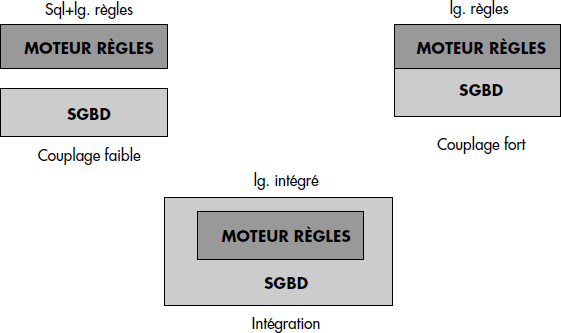
La réalisation d'un SGBD déductif nécessite donc l'intégration d'un moteur de règles au sein d'un SGBD. Celui-ci doit être capable de réaliser l'inférence nécessaire lors de l'interrogation, voire la mise à jour, des prédicats dérivés. Une fonctionnalité analogue à celle d'un SGBD déductif peut être obtenue en couplant un moteur de règles à un SGBD. On distingue le couplage faible où les deux composants restent visibles à l'utilisateur du couplage fort où seul le langage de règles est visible. La figure XV.1 illustre les techniques de couplage et d'intégration. Un SGBD déductif essaie donc de réaliser l'intégration forte, en offrant un langage intégré de définition et de manipulation de connaissances.

La réalisation d'un SGBD déductif intégré pose de nombreux problèmes. Tout d'abord, il faut définir le langage d'expression de connaissances. Nous étudions ci-dessous l'approche DATALOG, inspirée au départ du langage de programmation logique PROLOG, qui est devenue le standard de la recherche. Ensuite, il faut choisir le modèle interne de données pour stocker les faits, mais aussi pour stocker les règles. Plusieurs approches partent d'un SGBD relationnel, soit étendu, soit modifié. D'autres ont cherché à réaliser des SGBD déductifs à partir de SGBD objet [Abiteboul90, Nicolas97] intégrant les deux paradigmes. Ensuite, il faut garantir la cohérence des données et des règles : ce problème d'intégrité étendue est très important, car il est possible en théorie de déduire n'importe quoi d'une base de connaissances (faits + règles) incohérente. Enfin, il faut répondre aux questions de manière efficace, en réalisant l'inférence à partir des faits et des règles, sans générer de faits inutiles ni redondants, mais aussi sans oublier de réponses. Le problème de l'efficacité du mécanisme d'inférence en présence d'un volume important de faits et de règles, notamment récursives, est sans doute l'un des plus difficiles.

Dans le contexte logique, une base de données est perçue comme un ensemble de prédicats. Les extensions des prédicats extensionnels sont matérialisées dans la base de données. Les prédicats extensionnels correspondent aux relations du modèle relationnel.

Une base de données est manipulée par des programmes logiques constitués d'une suite de clauses de Horn qui définissent des prédicats intentionnels. Un prédicat intentionnel est donc défini par un programme de règles logiques ; il correspond à une vue du modèle relationnel.

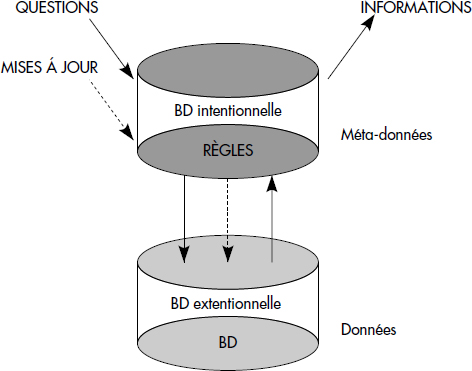
Une base de données logique est constituée d'un ensemble de prédicats extensionnels constituant la base de données extensionnelle et d'un ensemble de prédicats intentionnels constituant la base de données intentionnelle. Les règles permettant de calculer les instances des prédicats intentionnels sont donc partie intégrante de la base de données logique. Elles sont écrites dans le langage DATALOG basé sur les clauses de Horn. La figure XV.2 illustre les notions de bases de données extensionnelle et intentionnelle, la seconde étant dérivée de la première par des règles stockées dans la métabase du SGBD.

Le SGBD est dit déductif, car il permet de déduire des informations à partir de données stockées par utilisation d'un mécanisme d'inférence logique. Les informations sont les tuples des prédicats intentionnels ; elles peuvent être déduites lors de l'interrogation des prédicats intentionnels ou lors des mises à jour des prédicats extensionnels. La mise à jour des prédicats intentionnels est difficile : il faut théoriquement répercuter sur les prédicats extensionnels, ce qui nécessite une extension des mécanismes de mise à jour au travers de vues.

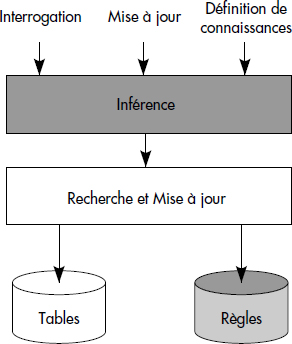
En résumé, un SGBD déductif va donc comporter un noyau de SGBD permettant de stocker faits et règles dans la base, et d'exécuter des opérateurs de base comme un SGBD classique. Au-delà, il va intégrer des mécanismes d'inférence pour calculer efficacement les faits déduits. Un langage intégré de définition et manipulation de connaissances permettra la définition des tables, des règles, l'interrogation et la mise à jour des informations (voir figure XV.3).

Outre la définition des prédicats extensionnels, DATALOG permet d'écrire les clauses de Horn spécifiant les prédicats intentionnels. L'alphabet utilisé est directement dérivé de celui de la logique du premier ordre. Il est composé des symboles suivants :

1. Des variables dénotées x, y, z … ;
2. Des constantes choisies parmi les instances des types de base entier, numérique et chaîne de caractères ;
3. Des prédicats relationnels dénotés par une chaîne de caractères, chaque prédicat pouvant recevoir un nombre fixe d'arguments (n pour un prédicat n-aire) ;
4. Les prédicats de comparaison =, <, >, ≤, ≥, ≠ ;
5. Les connecteurs logiques « et » dénoté par une virgule (,) et « implique » que l'on interprète de la droite vers la gauche, dénoté par le signe d'implication inversé (←).

À partir de cet alphabet (celui de la logique des prédicats du premier ordre particularisé et réduit), on construit des formules particulières qui sont des clauses de Horn ou règles DATALOG. Un terme est ici soit une constante, soit une variable. Un atome (aussi appelé formule atomique ou littéral positif) est une expression de la forme P(t1,t2…tn), où P est un prédicat n-aire. Un atome instancié est un atome sans variable (les variables ont été remplacées par des constantes). À partir de ces concepts, une règle est définie comme suit :

Q est appelé tête de règle ou conclusion ; P1, P2… Pn est appelé corps de règle ou prémisse ou encore condition. Chaque Pi est appelé sous-but. En appliquant l'équivalence Q ← P ⇔ ¬ P ∨ Q, une règle s'écrit aussi ¬ (P1, P2…Pn) ∨ Q ; puis en appliquant ¬ (P1, P2) ⇔ ¬ P1 ∨ ¬ P2, on obtient ¬ P1 ∨ ¬ P2 ∨ … ¬ Pn ∨ Q. Donc, une règle est une clause de Horn avec au plus un littéral positif (la tête de règle Q).

La figure XV.4 donne un exemple de programme DATALOG définissant une base de données extensionnelle décrivant les employés (prédicat extensionnel EMPLOYE) et les services (prédicat extensionnel SERVICE) d'une grande entreprise. La base de données intentionnelle spécifie le chef immédiat de chaque employé (prédicat DIRIGE1), puis le chef du chef immédiat (prédicat DIRIGE2).

{
    /* Déclaration des prédicats extensionnels */
    EMPLOYE(NomService : String, NomEmploye : String);
    SERVICE(NomService : String, NomChef : String);
    /* Définition des prédicats intentionnels */
    DIRIGE1(x,y) ← SERVICE(z,x), EMPLOYE(z,y)
    DIRIGE2(x,y) ← DIRIGE1(x,z), DIRIGE1(z,y)
}

Un autre exemple de programme DATALOG est présenté figure XV.5. Il définit une base de données extensionnelle composée de pays et de vols aériens reliant les capitales des pays. La base de données intentionnelle permet de calculer les capitales proches (prédicat CPROCHE) comme étant les capitales atteignables l'une depuis l'autre en moins de cinq heures dans les deux sens. Les pays proches (prédicat PPROCHE) sont ceux ayant des capitales proches.

{
    /* Déclaration des prédicats extensionnels */
    PAYS(Nom : String, Capitale : String, Pop : Int);
    VOLS(Num : Int, Depart : String, Arrivee : String, Duree : Int);
    /* Définition des prédicats intentionnels */
    CPROCHE(x,y) ← VOLS(z,x,y,t), t≤5, VOLS(w,y,x,u), u≤5;
    PPROCHE(x,y) ← PAYS(x,u,p), PAYS(y,v,q), CPROCHE(u,v);
}

Parmi les règles, il en existe une classe particulièrement importante par la puissance qu'elle apporte au langage : il s'agit des règles récursives qui permettent de définir un prédicat intentionnel en fonction de lui-même.

Une règle récursive dont le prédicat de tête apparaît une seule fois dans le corps est dite linéaire. Une règle non linéaire est quadratique si le prédicat de tête apparaît deux fois dans le corps. Au-delà, une règle récursive dont le prédicat de tête apparaît n (n ≥ 3) fois dans le corps devient difficilement compréhensible.

La figure XV.6 illustre quelques exemples de règles récursives.

{
    /* Dirige à tout niveau spécifié par une règle récursive linéaire */
    DIRIGE(x,y) ← DIRIGE1(x,y) ;
    DIRIGE(x,y) ← DIRIGE1(x,z), DIRIGE(z,y) ;
    /* Dirige à tout niveau spécifié par une règle récursive quadratique */
    DIRIGE(x,y) ← DIRIGE1(x,y) ;
    DIRIGE(x,y) ← DIRIGE(x,z), DIRIGE(z,y) ;
    /* Liaisons effectuables par étapes de moins de 5 heures */
    LIAISON(x,y) ← VOLS(z,x,y,t), t ≤ 5 ;
    LIAISON(x,y) ← LIAISON(x,z), LIAISON(z,y) ;
}

Chaque relation récursive nécessite une règle d'initialisation non récursive, puis une règle de calcul récursive. Le premier couple de règles définit qui dirige qui, et ce à tout niveau. Le deuxième définit la même relation, mais en utilisant une règle non linéaire. Le dernier couple spécifie les liaisons aériennes possibles entre capitales par des suites de liaisons simples effectuées en moins de cinq heures.

La figure XV.7 spécifie en DATALOG la célèbre base de données des familles à partir des prédicats extensionnels PERE et MERE indiquant qui est père ou mère de qui. La relation récursive ANCETRE a souvent été utilisée pour étudier les problèmes de la récursion. Nous avons ajouté la définition des grand-parents comme étant les parents des parents et celle des cousins comme étant deux personnes ayant un ancêtre commun. Les amis de la famille (AMIF) sont les amis (prédicat extensionnel AMI) ou les amis de la famille des parents. Les cousins de même génération (prédicat MG) se déduisent à partir des frères ou sœurs. Notez que cette définition est large : elle donne non seulement les cousins, mais aussi soi-même avec soi-même (vous êtes votre propre cousin de niveau 0 !), les frères et sœurs, puis vraiment les cousins de même génération.

{
    /* Prédicats extensionnels Père, Mère et Ami */
            PERE(Père String, Enfant String)
            MERE(Mère String, Enfant String)
            AMI(Personne String, Personne String)
    /* Parent comme union de père et mère */
            PARENT(x,y) ← PERE(x,y);
            PARENT(x,y) ← MERE(x,y);
    /* Grand-parent par auto-jointure de parents */
            GRAND-PARENT(x,z) ← PARENT(x,y), PARENT(y,z);
    /* Ancêtre défini par une règle linéaire */
            ANCETRE(x,y) ← PARENT(x,y);
            ANCETRE(x,z) ← ANCETRE(x,y), PARENT(y,z);
    /* Cousin à partir d'ancêtres */
            COUSIN(x,y) ← ANCETRE(z,x), ANCETRE(z,y);
    /* Ami de la famille comme ami des ancêtres */
            AMIF(x,y) ← AMI(x,y);
            AMIF(x,y) ← PARENT(x,z), AMIF(z,y);
    /* Cousins de même génération à partir des parents */
            MG(x,y) ← PARENT(z,x), PARENT(z,y);
            MG(x,y) ← PARENT(z,x),MG(z,u),PARENT(u,y);
}

Plus généralement, une relation récursive est une relation définie en fonction d'elle-même. Une relation récursive n'est pas forcément définie par une règle récursive. En effet, des règles mutuellement récursives permettent de définir une relation récursive. Plus précisément, il est possible de représenter la manière dont les prédicats dépendent l'un de l'autre par un graphe de dépendance. Les sommets du graphe sont les prédicats et un arc relie un prédicat P à un prédicat Q s'il existe une règle de tête Q dans laquelle P apparaît comme un sous-but. Un prédicat intentionnel est récursif s'il apparaît dans un circuit. La figure XV.8 illustre un programme DATALOG avec récursion mutuelle. Le prédicat R est récursif.

{
    R(x,y) ← B(x,y);
    R(x,y) ← P(x,z), B(z,y);
    P(x,y) ← R(x,z), C(z,y);
}

En résumé, un programme DATALOG est un ensemble de règles. On note les règles constituant un programme entre crochets {}, chaque règle étant séparée de la suivante par un point virgule. L'ordre des règles est sans importance. Les prédicats relationnels sont classés en prédicats extensionnels dont les instances sont stockées dans la base sur disques, et en prédicats intentionnels qui sont les relations déduites (ou dérivées). DATALOG permet aux utilisateurs de définir à la fois des règles et des faits, un fait étant simplement spécifié comme une règle à variable instanciée sans corps (par exemple, PERE (Pierre,Paul)). Bien que la base extensionnelle puisse être définie en DATALOG comme une suite de prédicats, nous admettrons en général qu'elle est créée comme une base relationnelle classique, par exemple en SQL. Ainsi, DATALOG sera plutôt utilisé pour spécifier des règles, avec des corps et des têtes. Le couple base de données extensionnelle-base de données intentionnelle écrit en DATALOG constitue une base de données déductive définie en logique.

La sémantique d'un programme DATALOG (c'est-à-dire ce que calcule ce programme) peut être définie de plusieurs manières. Nous examinons ci-dessous les trois techniques les plus courantes.

XX-3-2-1. Théorie de la preuve▲

DATALOG dérivant de la logique, il apparaît naturel d'utiliser une méthode de preuve pour calculer les instances des prédicats intentionnels. On aboutit alors à l'approche sémantique de la preuve. Dans cette approche, un programme DATALOG calcule tout ce qui peut être prouvé en utilisant la méthode de preuve par résolution [Lloyd87]. Un fait non prouvable est considéré comme faux.

Notion XV.7 : Sémantique de la preuve (Proof theoretic semantics)

Sémantique selon laquelle un fait est vrai s'il peut être prouvé en appliquant la méthode de résolution à partir des axiomes logiques dérivés d'un programme DATALOG.

Afin d'illustrer la méthode, considérons la base de données définie figure XV.4, contenant :

1. Le prédicat extensionnel EMPLOYE avec deux tuples <informatique-Julie> et <informatique-Pierre> indiquant que Pierre et Julie sont deux employés du département informatique ;
2. Le prédicat extensionnel SERVICE avec un tuple <informatique-Pierre> indiquant que Pierre est le chef du service informatique.

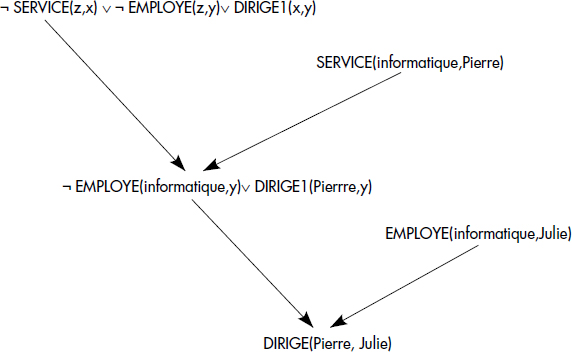
Pour savoir si le tuple <Pierre-Julie> appartient logiquement au prédicat intentionnel DIRIGE1, il suffit d'appliquer la méthode de résolution pour prouver le théorème DIRIGE1 (Pierre,Julie) à partir des axiomes dérivés des relations de base EMPLOYE (informatique,Julie), EMPLOYE (informatique,Pierre) et de celui dérivé de la règle DIRIGE1(x,y) ← SERVICE(z,x), EMPLOYE(z,y). Ce dernier axiome se réécrit, en éliminant l'implication, DIRIGE1(x,y)∨ ¬SERVICE(z,x)∨ ¬EMPLOYE (z,y). L'arbre de preuve permettant de conclure que <Pierre-Julie> est un fait vrai (c'est-à-dire un tuple de DIRIGE1) est représenté figure XV.9.

En résumé, la méthode de résolution permet de donner une sémantique à un programme DATALOG : un fait appartient à un prédicat intentionnel s'il peut être prouvé comme un théorème par résolution. En cas d'échec de la méthode, le fait est supposé faux : il n'appartient pas au prédicat intentionnel. Cette interprétation de l'absence de preuve est appelée négation par échec. La méthode ainsi complétée est appelée méthode de résolution avec négation par échec (ou encore méthode SLDNF). Il s'agit d'une méthode qui permet de déterminer si un tuple appartient ou non à un prédicat intentionnel. C'est donc une méthode essentiellement procédurale qui fonctionne tuple à tuple. Elle est proche des méthodes de calcul appliquées par les interpréteurs PROLOG.

XX-3-2-2. Théorie du modèle▲

EMPLOYE (informatique,Pierre),
EMPLOYE (informatique,Julie),
SERVICE (informatique, Pierre)

DIRIGE1 (x,y) ← SERVICE (z,x), EMPLOYE (z,y)

{ EMPLOYE (informatique,Pierre), EMPLOYE (informatique,Julie), SERVICE (informatique,Pierre), DIRIGE1 (Pierre,Julie), DIRIGE1 (Pierre,Pierre) } ;

{ EMPLOYE (informatique,Pierre), EMPLOYE (informatique,Julie), SERVICE (informatique,Pierre), DIRIGE1 (Pierre,Julie), DIRIGE1 (Pierre,Pierre), DIRIGE1 (Julie,Julie)} ;

{ EMPLOYE (informatique,Pierre), EMPLOYE (informatique,Julie),
  SERVICE (informatique,Pierre), DIRIGE1 (Pierre,Julie),
  DIRIGE1 (Pierre,Pierre) }

XX-3-2-3. Théorie du point fixe▲

EMPINF(x,y) ← EMPLOYE(x,y), x = informatique;
EMPINF = EMPINF ∪ σA1=informatique (EMPLOYE)
DIRIGE1(x,y) ← SERVICE(z,x), EMPLOYE(z,y) ;
DIRIGE1 = DIRIGE1 ∪ ∏A2,A4 (σA1=A3 (SERVICE x EMPLOYE))
DIRIGE2(x,y) ← DIRIGE1(x,z), DIRIGE1(z,y) ;
DIRIGE2 = DIRIGE2 ∪ ∏A1,A4 (σA2=A3 (DIRIGE1 x DIRIGE1))
DIRIGE(x,y) ← DIRIGE1(x,y) ;
DIRIGE = DIRIGE ∪ DIRIGE1
DIRIGE(x,y) ← DIRIGE1(x,z), DIRIGE(z,y) ;
DIRIGE = DIRIGE ∪ ∏A1,A4 (σA2=A3 (DIRIGE1 x DIRIGE))

P = { PARENT(x,y) ← PERE(x,y);
      PARENT(x,y) ← MERE(x,y) ;
      ANCETRE(x,y) ← PARENT(x,y);
      ANCETRE(x,y) ← PARENT(x,z), ANCETRE(z,y); }

TP = { PARENT = PARENT ∪ PERE;
       PARENT = PARENT ∪ MERE;
       ANCETRE = PARENT;
       ANCETRE = ANCETRE ∪ ∏1,4 (PARENT ▷◁ ANCETRE); }

TP(⊥) = { PARENT (Jean,Pierre); PARENT (Pierre,Julie);
          ANCETRE (Jean,Pierre); ANCETRE (Pierre,Julie);
          ANCETRE (Jean, Julie)};

XX-3-2-4. Coïncidence des sémantiques▲

Jusque-là, les seuls axiomes dérivés d'une base de données extensionnelle sont des faits positifs (sans négation). Afin de permettre de répondre à des questions négatives (par exemple, qui n'est pas dirigé par Pierre ?), il apparaît nécessaire de compléter les axiomes avec des axiomes négatifs pour chaque fait qui n'apparaît pas dans la base. Cette dérivation d'axiomes négatifs, qui consiste à considérer que tout fait absent de la base est faux, est connue sous le nom d'hypothèse du monde fermé. Nous l'avons déjà introduite dans le chapitre V sur la logique. Nous la définissons plus précisément ici.

Ainsi, si la relation PERE (Père, Enfant) contient les faits PERE (Julie,Pierre) et PERE (Jean,Paul), on en déduit :

¬ PERE(Julie,Paul),   ¬ PERE (Julie,Jean), ¬ PERE (Julie,Julie),
¬ PERE(Pierre,Julie), ¬ PERE(Pierre,Jean), ¬ PERE(Pierre,Paul), etc.

L'hypothèse du monde fermé est une règle puissante pour inférer des faits négatifs. Elle suppose qu'un domaine peut prendre toutes les valeurs qui apparaissent dans la base (domaine actif) et que tous les faits correspondant à ces valeurs non connues sont faux [Reiter78]. Pour être valide, cette hypothèse nécessite des axiomes additionnels tels que l'unicité des noms et la fermeture des domaines [Reiter84].

Par exemple, en présence de valeurs nulles dans les bases de données, l'hypothèse du monde fermé est trop forte, car elle conduit à affirmer comme faux des faits inconnus. Les théoriciens se sont penchés sur des hypothèses plus fines, tolérant les valeurs nulles [Reiter84]. Une variante de l'hypothèse du monde fermée consiste à modifier la méthode de résolution permettant de répondre à une question en supposant faux tout fait qui ne peut être prouvé comme vrai. Cette approche est connue comme la négation par échec.

Il existe plusieurs raisons pour ajouter la négation à DATALOG ; en particulier, la négation est souhaitable pour pouvoir référencer l'inexistence d'un fait dans un prédicat. Elle permet de représenter la différence relationnelle ; elle est aussi utile pour exprimer des exceptions. Par exemple, lors d'un parcours de graphe, si l'on désire éviter le parcours des arcs enregistrés dans une relation INTERDIT (Origine, Extrémité), il est possible de compléter le programme de parcours comme suit :

{ CHEMIN(x,y) ← ARC(x,y), ¬INTERDIT(x,y) ;
  CHEMIN(x,y) ← CHEMIN(x,z),ARC(z,y), ¬INTERDIT(z,y) }

Plus généralement, l'introduction de la négation permet d'écrire des règles de la forme :

Q ← L1, L2… Ln

où Q est un littéral positif et L1, L2… Ln sont des littéraux positifs ou négatifs. Rappelons qu'un littéral négatif est une négation d'une formule atomique de la forme ¬P(t1,t2… tn), où P est un prédicat et t1, t2, …, tn sont des termes. Le langage DATALOG ainsi étendu avec des prédicats négatifs dans le corps de règle est appelé DATALOG^neg, encore noté DATALOG¬.

La sémantique d'un programme DATALOG^neg n'est pas facile à définir. En effet, l'intersection de modèles d'un tel programme n'est en général pas un modèle. Par exemple, le programme :

{ OISEAU (Pégase);
  PINGOIN(x) ← OISEAU(x), ¬VOLE(x);
  VOLE(x) ← OISEAU(x), ¬PINGOIN(x) }

a pour modèles :

• { OISEAU(Pégase); PINGOIN(Pégase) } et
• { OISEAU(Pégase); VOLE(Pégase) }

dont l'intersection { OISEAU(pégase) } n'est pas un modèle. Un tel programme n'a donc pas de plus petit modèle. En fait, en utilisant les équivalences logiques, les deuxième et troisième règles peuvent être réécrites :

VOLE(x) v PINGOIN(x) ← OISEAU(x)

Nous avons là une règle disjonctive qui introduit des informations ambiguës. D'où l'existence de plusieurs modèles possibles.

Sous certaines conditions syntaxiques, le problème du choix d'un modèle peut être résolu en divisant le programme en strates successives, chacune ayant un plus petit modèle [Apt86, Pryzymusinski88]. Un module d'un programme DATALOG étant un ensemble de règles, un programme stratifié peut être défini comme suit :

En fait, le plus petit modèle d'une strate est calculé à partir du plus petit modèle de la strate précédente, la négation étant remplacée par un test de non-appartenance. Si M est le plus petit modèle de la strate Si-1, ¬ P(x) est interprété comme « P(x) n'appartient pas à M » dans la strate Si.

Tout programme DATALOG n'est pas stratifiable ; il doit être possible de calculer complètement toute l'extension d'un prédicat avant d'utiliser sa négation pour pouvoir stratifier un programme. Cela n'est pas vrai si la récursion traverse la négation. Les programmes stratifiables ont un plus petit modèle unique qui est caractérisé en définissant un ordre partiel entre les prédicats. L'ordre correspond à un calcul de plus petit modèle strate par strate en utilisant l'hypothèse du monde fermé.

Par exemple, les programmes :

• {P(x) ← ¬ P(x)} et
• { PAIRE(0); IMPAIRE(x) ← ¬ PAIRE(x) ; PAIRE(x) ← ¬IMPAIRE(x) }

ne sont pas stratifiables, car la négation se rencontre sur un cycle de récursion (c'est-à-dire traverse la récursion). Le programme

• { R(1) ← ; P(1) ← ; P(2) ← ; Q(x) ← R(x); T(x) ← P(x),¬Q(x)}

est stratifiable ; deux strates possibles sont :

• S1 = {R(1) ← ; Q(x) ← R(x)} puis
• S2 = { P(1) ← ; P(2) ← ; T(x) ← P(x),¬ Q(x)};

S1 calcule Q sans utiliser ¬ Q, puis S2 calcule T en utilisant ¬ Q et P. Le plus petit modèle de S1 est {R(1); Q(1)}. Celui de S2 est {R(1); Q(1); T(2)}. Notez que l'ordre de calcul des prédicats est fondamental : si on commençait à calculer T avant Q, on obtiendrait T(1) et un résultat qui ne serait pas un modèle.

La négation en corps de règle est importante, car elle permet de réaliser la différence relationnelle. La stratification correspond à la sémantique couramment admise en relationnel : avant d'appliquer une différence à une relation, il faut calculer complètement cette relation (autrement dit, le « pipe-line » est impossible avec l'opérateur de différence).

Comme PROLOG, DATALOG est construit à partir des clauses de Horn. Aussi, les règles sont en principe limitées à des clauses de Horn pures, disjonctions d'un seul prédicat positif avec plusieurs prédicats négatifs (0 à n). Il n'y a pas de difficultés à étendre les têtes de règles à plusieurs prédicats positifs reliés par conjonction (et) ; une règle à plusieurs têtes est alors interprétée comme plusieurs règles à une seule tête avec le même corps. Une autre possibilité est de tolérer un prédicat négatif en tête de règle. Une information négative étant en général une information non enregistrée dans la base, une interprétation possible pour un tel prédicat est une suppression des faits correspondant aux variables instanciées satisfaisant la condition de la règle. Le langage DATALOG avec négation possible en corps et en tête de règle est appelé DATALOG^neg,^neg, encore noté DATALOG¬¬.

La négation en tête de règle est donc interprétée comme une suppression. C'est elle qui confère réellement la non-monotonie à des programmes DATALOG. Au-delà, il est possible de placer plusieurs prédicats en tête d'une règle DATALOG. Supporter à la fois les règles à têtes multiples et des prédicats négatifs en tête de règle conduit à permettre les mises à jour dans le langage de règles. On parle alors du langage DATALOG avec mise à jour, noté DATALOG*.

Par exemple, la règle suivante, définie sur la base de données intentionnelle { PARENT(Ascendant, Descendant), ANCETRE(Ascendant, Descendant) } est une règle DATALOG* :

ANCETRE(x,z), ¬ ANCETRE(z,x) ← PARENT(x,y), ANCETRE(y,z)

Cette règle génère de nouveaux ancêtres et supprime des cycles qui pourraient apparaître dans la relation ancêtre (si x est le parent de y et y l'ancêtre de z, alors x est l'ancêtre de z, mais z n'est pas l'ancêtre de x).

Une interprétation de DATALOG* est possible à partir des règles de production, très populaires dans les systèmes experts. Une règle de production est une expression de la forme :

<condition> → <expression d'actions>

Une expression d'actions est une séquence d'actions dont chacune peut être soit une mise à jour, soit un effet de bord (par exemple, l'appel à une fonction externe ou l'édition d'un message). Une condition est une formule bien formée de logique. Quand l'ordre d'évaluation des règles est important, celles-ci sont évaluées selon des priorités définies par des métarègles (des règles sur les règles) ; par exemple, une métarègle peut simplement consister à exécuter les règles dans l'ordre séquentiel. Ainsi, un langage de règles de production n'est pas complètement déclaratif, mais peut contenir une certaine procéduralité. Il en va de même pour les programmes DATALOG avec mises à jour.

Un programme DATALOG^* peut être compris comme un système de production [Kiernan90]. Chaque règle est exécutée jusqu'à saturation pour chaque instanciation possible des variables par des tuples satisfaisant la condition. Un prédicat positif en tête de règle correspond à une insertion d'un fait et un prédicat négatif à une suppression. Une règle peut à la fois créer des tuples et en supprimer dans une même relation. Plus précisément, soit une expression d'actions de la forme R(p1), R(p2)…, ¬ R(n1), ¬ R(n2)… avec des actions conflictuelles sur une même relation R. Notons P = {p1, p2…} l'ensemble des tuples insérés dans R et N = {n1, n2…} l'ensemble des tuples supprimés. Certains tuples pouvant être à la fois insérés et supprimés, il faut calculer l'effet net des insertions et suppressions. De sorte à éviter les sémantiques dépendant de l'ordre d'écriture des actions, l'opération effectuée peut être définie par : R = R - (N - P) ∪ (P - N). Ainsi, une telle expression d'actions effectue une mise à jour de la relation R ; l'ordre des actions dans l'expression est sans importance.

L'existence d'un point fixe pour un programme DATALOG^* n'est pas un problème trivial. Certaines règles peuvent supprimer des tuples que d'autres règles créent. Un programme de règles avec mises à jour peut donc boucler ou avoir différents états stables selon l'ordre d'application des règles, donc avoir une sémantique ambiguë. Un programme est confluent s'il conduit toujours au même résultat (point fixe), quel que soit l'ordre d'application des règles. Afin d'éviter les programmes à sémantique ambiguë, il est possible d'utiliser une métarègle implicite analogue à la stratification : une règle avec suppression sur une relation R ne peut être exécutée que quand toutes les règles insérant dans R ont été exécutées jusqu'à saturation. Une telle règle est très restrictive et impose par exemple de rejeter les règles à la fois insérant et supprimant (mises à jour).

Par exemple, pour démontrer la puissance de DATALOG ainsi étendu, nous proposons des règles de transformation de circuits électriques. Cet exemple suppose une base de données relationnelle composée d'une unique relation CIRCUIT(Nom, Fil, Origine, Extrémité, Impédance). Nom est le nom du circuit. Fil est un identifiant donné à chaque fil. Les origines et extrémités de chaque fil sont données par les attributs correspondants, alors que le dernier attribut donne l'impédance du circuit. Un problème typique est de calculer l'impédance du circuit. Pour cela, il faut appliquer les transformations série et parallèle, classiques en électricité. Chaque règle remplace deux fils par un fil qu'il faut identifier. Il faut donc pouvoir créer de nouveaux identifiants de fils, ce que nous ferons par une fonction de création d'objets à partir de deux objets existants f1 et f2, dénotée new (f1,f2). En conséquence, la règle suivante effectue la transformation parallèle (1/i = 1/i1 + 1/i2) :

¬ CIRCUIT(x,f1,o,e,i1),¬ CIRCUIT(x,f2,o,e,i2),
CIRCUIT(x,new(f1,f2),o,e,(i1*i2)/(i1+i2))
← CIRCUIT(x,f1,o,e,i1), CIRCUIT(x,f2,o,e,i2)

La transformation série est similaire, mais il faut s'assurer de la non-existence d'un fil partant de la jonction des deux fils en série, ce qui nécessite une négation en corps de règle. D'où la règle suivante qui cumule les impédances de deux fils en série :

¬ CIRCUIT(x,f1,o,e1,i1),¬ CIRCUIT(x,f2,e1,e,i2),
CIRCUIT(x,new(f1,f2),o,e,i1+i2)
← CIRCUIT(x,f1,o,e1,i1),CIRCUIT(x,f2,e1,e,i2),¬ CIRCUIT(x,f3,e1,e2,i3)

Ces deux règles réduisent les circuits par remplacement des fils en parallèle et en série appartenant à un même circuit par un fil résultat de la transformation effectuée. Notez qu'elles ne sont pas stratifiables. Cependant, le programme de règles est confluent, au moins pour des circuits électriques connexes.

D'autres sémantiques que la sémantique opérationnelle des règles de production introduite ci-dessus ont été proposées pour Datalog* [Abiteboul95], comme la sémantique inflationniste et la sémantique bien fondée. La sémantique inflationniste est simple : elle calcule les conditions, puis tous les faits déduits de toutes les règles à la fois. Elle applique donc un opérateur de point fixe global modifié. Malheureusement, le résultat ne correspond guère à la signification courante. La sémantique bien fondée est plus générale : elle est basée sur une révision de l'hypothèse du monde fermée, en autorisant des réponses inconnues à des questions. Pour Datalog^neg, elle coïncide avec la sémantique stratifiée lorsque les programmes sont stratifiables. Les problèmes de sémantique de Datalog* sont en résumé très difficiles et ont donné lieu à de nombreux travaux théoriques de faible intérêt.

Pour accroître la puissance de DATALOG, il est souhaitable d'intégrer les fonctions de la logique du premier ordre au langage. Des symboles de fonctions pourront alors être utilisés dans les arguments des prédicats, en tête ou en corps de règle. Des exemples de fonctions sont les fonctions arithmétiques (+, -, /, *) ou plus généralement des fonctions mathématiques (LOG, EXP, SIN…), voire des fonctions programmées par un utilisateur. Les fonctions sont importantes, car elles permettent en général la manipulation d'objets complexes [Zaniolo85], par exemple des figures géométriques. En général, les fonctions permettent d'invoquer des types abstraits de données [Stonebraker86].

D'un point de vue syntaxique, l'extension consiste à introduire dans l'alphabet des symboles de fonctions, notés f, g, h … Chaque fonction a une arité n, qui signifie que la fonction accepte n paramètres. De nouveaux termes peuvent être construits de la forme f(t1, t2, …, tn) où chaque ti est lui-même un terme (qui peut être construit en utilisant un symbole de fonction). Les termes fonctionnels peuvent être utilisés à l'intérieur d'un prédicat comme un argument. Le langage résultant est appelé DATALOG^fonc.

Ainsi, des prédicats tels que P(a,x,f(x),f(g(x,a))) où f est une fonction unaire et g une fonction binaire sont acceptés. La sémantique de DATALOG doit alors être complétée pour intégrer les fonctions. Cela s'effectue comme en logique, en faisant correspondre à chaque fonction n-aire une application de Dⁿ dans D, D étant le domaine d'interprétation.

Les fonctions sont très utiles en pratique pour effectuer des calculs. Par exemple, un problème de cheminement avec calcul de distance sur un graphe pourra être exprimé comme suit :

{ CHEMIN(x,y,d) ← ARC(x,y,d) ;
  CHEMIN(x,y,d+e) ← CHEMIN(x,z,e), ARC(z,y,d) }

La recherche des longueurs de tous les chemins allant de Paris à Marseille s'effectuera par la requête ? CHEMIN(Paris,Marseille,x).

Un problème qui devient important avec DATALOG^fonc est celui de la finitude des réponses aux questions (ou des relations déduites). Une question est saine (en anglais safe) si elle a une réponse finie indépendamment des domaines de la base (qui peuvent être finis ou infinis). Le problème de déterminer si une question est saine existe déjà en DATALOG pur. Si les domaines sont infinis, un programme DATALOG peut générer des réponses infinies. Par exemple, le programme :

{ SALAIRE(100) ;
  SUPERIEUR(x,y) ← SALAIRE(x), x < y ;
  ? SUPERIEUR(x,y) }

génère une réponse infinie. Pour éviter des programmes a modèle infini, une caractérisation syntaxique des programmes sains a été proposée [Zaniolo86]. Cette caractérisation est basée sur la notion de règle à champ restreint. Une règle est à champ restreint si toutes les variables figurant en tête de règle apparaissent dans un prédicat relationnel dans le corps de la règle. Par exemple, la règle SUPERIEUR(x,y) ← SALAIRE(x), x < y n'est pas à champ restreint, car y n'apparaît pas dans un prédicat relationnel dans le corps de la règle. Si toutes les règles d'un programme DATALOG sans fonction sont à champ restreint, alors le programme est sain et ne peut générer des réponses infinies.

Avec des fonctions, le problème de savoir si un programme est sain est plus difficile. Par exemple, le programme :

{ ENTIER(0);
  ENTIER(x+1) ← ENTIER(x) }

n'est pas sain, car il génère un prédicat infini (les entiers positifs sont générés dans ENTIER). Cependant, ce programme est à champ restreint. Notez cependant que la question ? ENTIER(10) a une réponse finie unique (vrai). Vous trouverez une méthode générale pour déterminer si un programme avec fonctions est sain dans [Zaniolo86].

En conclusion, il est intéressant de remarquer qu'il est possible d'étendre l'algèbre relationnelle avec des fonctions [Zaniolo85], comme vu dans le chapitre XI sur le modèle objet. En fait, il est nécessaire d'inclure des fonctions dans les qualifications de jointures et restrictions (les qualifications sont alors des expressions de logique du premier ordre avec fonctions). Il est aussi nécessaire d'inclure des fonctions dans les critères de projection. On projette alors sur des termes fonctionnels calculés à partir d'attributs. Le plus petit modèle d'un programme DATALOG^fonc peut alors être calculé par un programme utilisant des boucles d'expressions d'algèbre relationnelle sans différence. Ainsi, DATALOG^fonc a la puissance de l'algèbre relationnelle avec fonction sans différence, mais avec la récursion. Pour avoir la différence, il faut passer à DATALOG^fonc,neg et pour avoir les mises à jour à DATALOG^fonc,*.

Une caractéristique intéressante des langages de manipulation de bases de données relationnelles comme SQL est la possibilité de manipuler des ensembles à travers des fonctions agrégats. Plusieurs auteurs ont proposé d'introduire les ensembles dans les langages de règles [Zaniolo85, Beeri86, Kupper86]. Le but est de supporter des attributs multivalués contenant des ensembles de valeurs. DATALOG étendu avec des ensembles est appelé DATALOG^ens.

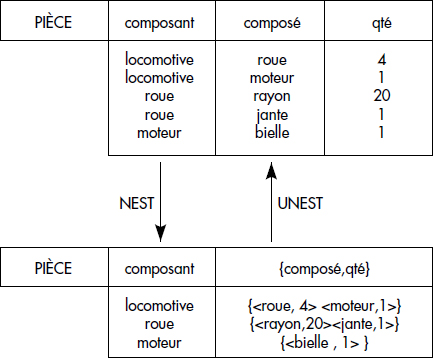
Afin d'illustrer l'intérêt des ensembles, considérons la relation de schéma PIECE(COMPOSE, COMPOSANT) dont un tuple <a,b> exprime le fait que a est composé avec le composant b. Pour une pièce donnée a, il existe autant de tuples que de composants de a dans cette relation. Trouver toutes les sous-pièces de chaque pièce et les répertorier dans une relation COMPOSE(PIECE, ENSEMBLE_DE_SOUSPIECE) est une opération intéressante, possible dès que l'on tolère des attributs multivalués. Une telle opération est appelée groupage (en anglais, nest). L'opération inverse est le dégroupage (en anglais, unest). Ces deux opérations déjà étudiées dans le chapitre XI sur le modèle objet sont illustrées figure XV.11.

Il existe plusieurs manières d'introduire les ensembles dans un langage de règles. Il est possible d'introduire de nouveaux domaines dans la base de données intentionnelle dont les valeurs sont des ensembles de constantes. Cependant, il est sage d'interdire les ensembles d'ensembles, donc de se limiter à un niveau d'ensemble ; dans le cas contraire, il serait possible de générer des ensembles d'ensembles à des profondeurs infinies. Pour éviter de confondre les variables qui référencent des ensembles avec celles qui référencent des valeurs simples, nous utiliserons des majuscules pour les variables d'ensembles et des minuscules pour les variables simples, comme [Kuper86].

Pour accomplir l'opération de groupage, un opérateur spécial appelé groupage peut être introduit comme dans [Beeri86]. Le groupage range dans un ensemble toutes les valeurs des variables en arguments qui satisfont la condition du corps de règle. Appliqué à une variable x, le groupage est noté <x>. Ainsi, la relation COMPOSE résultat du groupage de la relation PIECE illustrée figure XV.11 peut être déclarée comme suit :

COMPOSE (x,Y) ← PIECE(x,y), Y = <y>

Étant donnés des ensembles et des éléments, un prédicat d'appartenance, noté ∈, peut être introduit. En utilisant ce prédicat, le dégroupage illustré figure XV.11 est exécuté par la règle :

PIECE(x,y) ← COMPOSE(x,Y), y ∈ Y.

Afin de comparer des ensembles, d'autres prédicats classiques peuvent être introduits, comme l'inclusion stricte notée ⊂. Des fonctions sur ensembles sont aussi possibles, telles que les fonctions agrégats classiques COUNT, MIN, MAX, AVG… qui délivrent des valeurs simples, ou des fonctions binaires entre ensembles qui délivrent des ensembles (∪, ∩, -).

Remarquons que le groupage ne donne pas plus de puissance au langage que les fonctions interprétées et la négation. En fait, si l'on définit la fonction unaire interprétée qui à un élément fait correspondre un ensemble composé de cet élément {}: x → {x} et la fonction binaire interprétée sur ensemble ∪: X,Y → X ∪ Y (c'est-à-dire l'union classique), il est possible d'effectuer le groupage par les règles suivantes :

SOUS-PIECE (x,Y) ← PIECE (x,y), Y = {y}
SOUS-PIECE (x,Y) ← SOUS-PIECE (x,Z), SOUS-PIECE (x,T), Y = Z ∪ T
COMPOSE (x,Y) ← SOUS-PIECE (x,Y), ¬SOUS-PIECE (x,Z), Z ⊂ Y

En clair, la deuxième règle fait l'union de tous les éléments composant chaque pièce x et la dernière garde le plus grand ensemble de sous-pièces Y ainsi généré. Il va de soi qu'utiliser l'opérateur de groupage est plus simple ; aussi, si le système réalise efficacement cet opérateur, il sera probablement plus performant pour effectuer le groupage qu'en exécutant les trois règles ci-dessus.

Pour conclure sur les ensembles, notons que l'introduction d'ensembles en DATALOG nécessite la stratification pour définir la sémantique d'un programme sans ambiguïté. Cela provient du fait que les ensembles intègrent un cas particulier de négation. La sémantique de la stratification nécessaire peut être exprimée comme suit : « calculer tout ensemble avant d'utiliser son contenu ». Ainsi, les règles doivent être partiellement ordonnées en strates dans lesquelles les opérations de groupage sont effectuées dès que possible. Si des groupages sont effectués dans des cycles de calculs de prédicats récursifs, le programme n'est pas stratifiable et a une sémantique ambiguë : il doit être rejeté.

La solution la plus simple pour répondre à une question portant sur un prédicat déduit par un programme DATALOG est de calculer ce prédicat, puis de le filtrer avec la question. Le calcul du prédicat peut se faire par calcul de point fixe comme vu formellement ci-dessus, lors de l'étude de la sémantique du point fixe. Ce calcul commence à partir des prédicats de base contenant les faits et génère des faits dans les prédicats dérivés par application successive des règles. Pour appliquer une règle, les variables sont instanciées avec des faits connus. Cela nécessite d'évaluer la condition composant le corps de règle sur les faits connus ; pour chaque instance des variables satisfaisant la condition, l'action (ou les actions) définie par le prédicat de tête est exécutée. La procédure de génération est appliquée jusqu'à saturation, c'est-à-dire jusqu'au point où aucune règle ne peut produire de nouveau fait. Une telle procédure est connue en intelligence artificielle comme la génération en chaînage avant [Nilsson80]. Elle est résumée figure XV.12.

{ Tant que « Il existe une relation dérivée R non saturée » faire{
  « sélectionner une règle r, dont l'action s'applique sur R » ;
  pour chaque « tuple de la base satisfaisant la condition de r » faire
      « exécuter les actions de r » ;
  }
}

L'approche proposée part des données pour élaborer la réponse à l'usager. Pour cette raison, elle est souvent appelée méthode d'évaluation bottom-up.

Une illustration de la génération bottom-up apparaît figure XV.13.

Une technique d'évaluation bottom-up calcule le plus petit modèle d'un programme logique ; donc, elle génère la base intentionnelle. La question est appliquée à la base intentionnelle. L'ordre et la manière selon lesquels les règles sont appliquées sont importants pour au moins deux raisons :

1. Ils peuvent changer les performances du processus de génération. Puisque les règles peuvent interagir de différentes manières (le résultat d'une règle peut changer la valeur de la condition d'une autre), il est souhaitable de choisir un ordre. Dans le cas de DATALOG pur, le problème du choix de l'ordre des règles est une extension de l'optimisation de question des SGBD relationnels.
2. Dans le cas de règles avec négations ou ensembles et de programmes stratifiés, il est nécessaire de générer chaque strate dans l'ordre de stratification pour obtenir un modèle correct. Plus complexe, avec des langages de règles de production (règles avec mises à jour), le résultat peut dépendre de l'ordre d'application des règles.

Au lieu de partir de la base extensionnelle pour générer les réponses aux questions, il est possible de partir de la question. Le principe est d'utiliser le profil de la question (nom de prédicat et valeurs connues) et de le remonter via les règles en chaînage arrière jusqu'à la base extensionnelle pour déterminer les faits capables de générer des réponses. Un tel procédé est connu sous le nom chaînage arrière en intelligence artificielle [Nilsson80]. Si des faits de la base sont retrouvés en utilisant le chaînage arrière, alors la question est satisfaite ; donc, une réponse oui/non est facile à élaborer en chaînage arrière. Plus généralement, la remontée des constantes de la question vers les tuples de la base permet de générer des faits relevants, seuls capables de produire des réponses aux questions [Lozinskii86].

Les faits relevants peuvent être utilisés afin de générer toutes les réponses à la question si nécessaire, en appliquant une procédure de chaînage avant à partir de ces faits. Cependant, la technique est très différente de l'évaluation bottom-up puisqu'elle profite des constantes de la question pour réduire les espaces de recherche. La méthode part de la question de l'usager pour remonter aux faits de la base. En conséquence, elle est appelée méthode top-down.

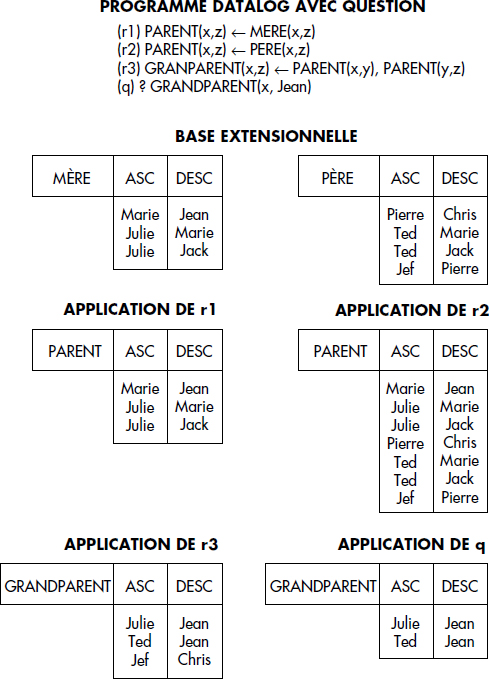
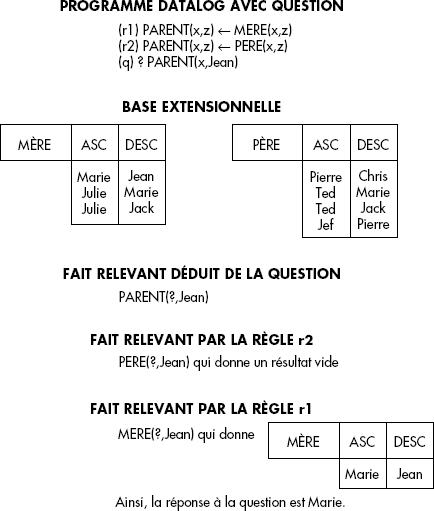
Une évaluation top-down de la question PARENT(x,Jean) est représentée figure XV.14. La question GRANDPARENT(x,Jean) de la figure XV.13 est plus difficile à évaluer. En première approche, tous les faits seront considérés comme relevants du fait de la règle (r3) (aucune variable ne peut être instanciée en chaînage arrière dans la première occurrence du prédicat PARENT). Le problème de déterminer précisément les faits relevants est difficile et nous l'étudierons plus généralement pour les règles récursives dans la section suivante.

La méthode d'évaluation top-down est formellement basée sur la méthode de résolution. Soit ? R(a,y) une question portant sur un prédicat dérivé R. Toute règle du type suivant :

R(..) ← B1,B2…Q1,Q2…

dont la conclusion peut être unifiée par une substitution µ avec la question permet de calculer une résolvante de la question. Pour chaque règle de ce type, une sous-question {B1,B2…Q1,Q2…}_[µ] est générée. Le processus doit être répété pour les sous-questions Q1_[µ], Q2_[µ]… Dans le cas où aucune relation n'est récursive, on finit toujours par aboutir à des sous-questions portant sur les prédicats de base B1,B2… qui peuvent être évaluées par le SGBD ; la collecte des résultats permet d'élaborer les réponses à la question initiale.

En résumé, la dérivation top-down transmet les constantes depuis la question vers la base afin de filtrer les faits relevants. Malheureusement, la remontée des constantes qui réduit grandement les espaces de recherche n'est en général pas simple. Elle demande de comprendre les connexions entre les règles dans un programme de règles, c'est-à-dire les unifications possibles entre prédicats. Dans ce but, plusieurs représentations par des graphes d'un programme DATALOG ont été proposées.

Toute règle peut être interprétée comme une production relationnelle. Les conditions dans le corps de règle représentent des restrictions (conditions de la forme x θ v, où θ est un opérateur de comparaison et v une valeur), des jointures (présences d'une même variable dans deux prédicats relationnels), des différences (négations de prédicats relationnels). Les implications correspondent à des projections. Plusieurs règles générant le même prédicat correspondent à une union. Il est donc possible de représenter un programme de règle DATALOG^neg par un graphe d'opérations relationnelles. Le graphe est un arbre dans le cas où aucun prédicat n'est récursif.

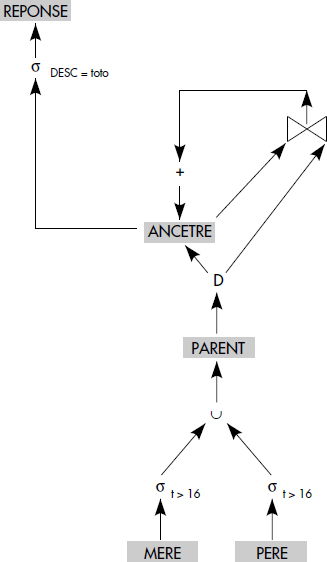
Le type de nœud correspondant à chaque opération relationnelle est représenté figure XV.15. Une duplication est simplement une recopie en un ou plusieurs exemplaires d'un résultat intermédiaire. Une addition est une union d'une relation avec la relation cible (cas particulier d'union dans laquelle le résultat est cumulé dans une des deux relations). Un arbre est généré par combinaison de ces nœuds. La figure XV.16 illustre la méthode de construction pour les règles suivantes :

• (r1) PARENT(x,z) ← MERE(x,t,z), t >16
• (r2) PARENT(x,z) ← PERE(x,t,z), t > 16
• (r3) ANCETRE(x,z) ← PARENT(x,z)
• (r4) ANCETRE(x,z) ← ANCETRE(x,y), PARENT(y,z)
• (r5) REPONSE(x) ← ANCETRE(x,toto)

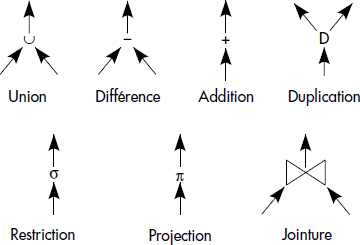
Notez qu'en général, la possibilité de compléter le graphe par un opérateur de duplication permet d'éviter de dupliquer des branches similaires de l'arbre et d'optimiser l'exécution correspondante. Par exemple, si l'on ajoute la règle :

• (r0) AIME(x,z) ← MERE(x,t,z), t >16

il n'est pas nécessaire de dupliquer toute la branche de restriction sur mère, mais seulement d'introduire un opérateur de duplication au niveau du résultat de cette branche. Celui-ci génère les tuples de AIME. Soulignons aussi que le nom d'un prédicat intermédiaire peut être omis lorsque ce dernier ne doit pas être gardé. Finalement, un graphe d'opérateurs relationnels donne un moyen de générer par simple traduction un programme bottom-up calculant la réponse à une question déductive. Tout le problème d'optimisation de questions déductives peut être vu comme un problème d'optimisation de graphes relationnels. Pour résumer, nous définirons informellement la notion de graphe relationnel de règles comme suit :

Le modèle le plus connu vient de l'intelligence artificielle, où il est utilisé pour représenter l'exécution de règles en chaînage arrière. Il s'agit des arbres ET/OU.

Étant donné un programme DATALOG sans négation et une question, un arbre ET/OU est construit comme suit. Chaque occurrence de prédicat est représentée par un ou plusieurs nœuds OU. Une règle correspond à un ou plusieurs nœuds ET. La racine de l'arbre est le prédicat de la question, donc un nœud OU. Les enfants d'un nœud OU sont toutes les règles dont la tête s'unifie avec le prédicat représenté par le nœud OU ; ce sont donc des nœuds ET. Les enfants d'un nœud ET sont toutes les occurrences des prédicats relationnels qui apparaissent dans le corps de la règle représentée. En principe, l'arbre est développé jusqu'à ce que les prédicats de la base extensionnelle apparaissent comme des feuilles. Pour spécifier les unifications (passages de paramètres) effectuées lorsque l'on passe d'une règle à une autre, la substitution qui unifie la tête de règle avec le prédicat parent (apparaissant dans le corps de la règle précédente) peut être mémorisée comme une étiquette sur l'arc allant du nœud représentant la règle au prédicat s'unifiant avec sa tête.

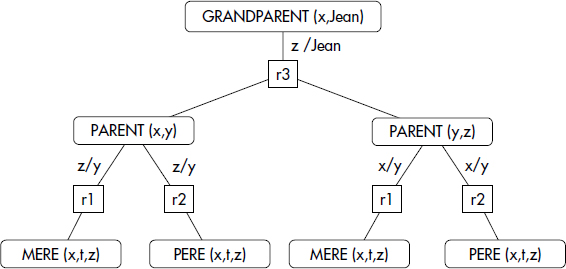
Par exemple, considérons le programme DATALOG suivant :

• (r1) PARENT(x,z) ← MERE(x,t,z)
• (r2) PARENT(x,z) ← PERE(x,t,z)
• (r3) GRANDPARENT(x,z) ← PARENT(x,y), PARENT(y,z)
• (q) ? GRANDPARENT(x,Jean)

L'arbre ET/OU associé à la résolution de la question (q) en dérivation top-down est représenté figure XV.17. Un nœud ET est représenté par un rectangle et un nœud OU par une ellipse.

Un arbre ET/OU montre la propagation des constantes depuis la question vers les relations de la base extensionnelle en chaînage arrière. Malheureusement, dans le cas de règles récursives, un arbre ET/OU peut devenir infini, car de nouvelles occurrences de règles sont ajoutées pour développer les nœuds qui correspondent à des relations récursives. Nous développerons la récursion dans la section suivante. Cependant, il apparaît déjà que des graphes plus sophistiqués sont nécessaires pour représenter les règles récursives.

Une extension de l'arbre ET/OU pour éviter les branches infinies en cas de prédicats récursifs est le graphe règle/but. Un graphe règle/but est aussi associé à une question qui spécifie un prédicat à évaluer. Il contient en outre des nœuds circulaires représentant les prédicats et des nœuds rectangulaires représentant les règles. Les seuls arcs d'un graphe règle/but sont définis par la règle suivante : s'il existe une règle r de la forme P ← P1, P2… Pn dans le programme de règles, alors il existe un nœud allant du nœud r au nœud P et, pour chaque Pi, il existe un arc allant du nœud Pi au nœud r. Dans sa forme la plus simple, un graphe règle/but peut être défini comme une variation d'un graphe ET/OU :

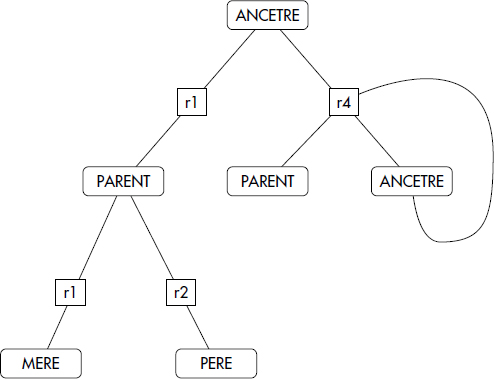
Ainsi, un graphe règle/but ne peut être infini. En présence de règles récursives, il contient simplement un cycle. Il correspond donc à un graphe ET/OU dans lequel une expansion déjà faite est remplacée par une référence à cette expansion. La figure XV.18 représente le graphe règle/but correspondant au programme suivant :

• { (r1) PARENT(x,z) ← MERE(x,t,z), t >16
•   (r2) PARENT(x,z) ← PERE(x,t,z), t > 16
•   (r3) ANCETRE(x,z) ← PARENT(x,z)
•   (r4) ANCETRE(x,z) ← ANCETRE(x,y), PARENT(y,z) }

Plusieurs autres représentations graphiques d'un ensemble de règles ont été proposées, parmi lesquelles les graphes de connexion de prédicats (PCG) [McKay81] et les réseaux de Petri à prédicats (PrTN) [Gardarin85, Maindreville87].

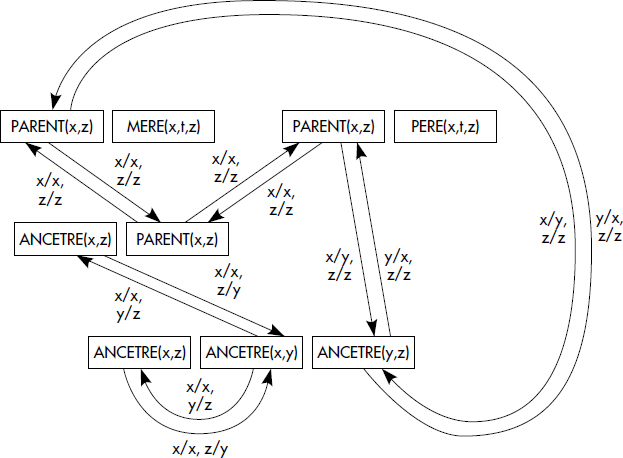
Un graphe de connexion de prédicats (PCG) modélise toutes les unifications possibles entre les prédicats d'un programme de règles. Plus précisément, une règle est modélisée comme un nœud multiple du PCG ; un tel nœud est représenté par un rectangle contenant le prédicat de tête puis les prédicats du corps. Un arc représente une unification entre un prédicat apparaissant en tête de règle et un prédicat apparaissant dans le corps d'une règle ; un arc est orienté et étiqueté par la substitution de variables réalisant l'unification. La figure XV.19 représente le PCG associé au programme :

• (r1) PARENT(x,z) ← MERE(x,t,z)
• (r2) PARENT(x,z) ← PERE(x,t,z)
• (r3) ANCETRE(x,z) ← PARENT(x,z)
• (r4) ANCETRE(x,z) ← ANCETRE(x,y), PARENT(y,z)

Un PCG actif correspond à un parcours simulant le chaînage arrière du PCG à partir d'une question représentée comme un nœud singulier sans tête [McKay81].

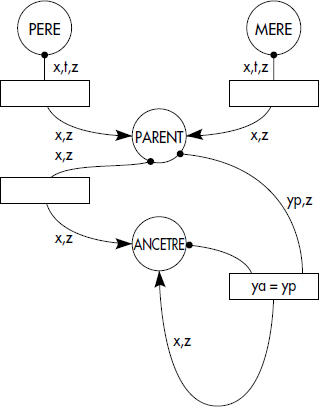
Un réseau de Petri à prédicats (PrTN) modélise directement une évaluation bottom-up (en chaînage avant) d'un programme de règles. Chaque relation (prédicat intentionnel ou extensionnel) est modélisée par une place ; les jetons de marquage correspondent aux tuples des relations. Chaque règle est modélisée par une transition ; le prédicat correspond à la condition de la règle. Les règles génèrent en sortie de nouveaux jetons (tuples) ; pour repérer quels jetons sont générés, on étiquette en général les arcs sortant des transitions avec des variables qui représentent les attributs des tuples générés. Les arcs entrants sont aussi étiquetés afin de faciliter l'écriture des conditions. Une exécution du PrTN modélise un calcul de point fixe en chaînage avant. Afin d'éviter la destruction des tuples dans les places lors d'un déclenchement d'une transition, il faut ajouter un arc qui remet le jeton après exécution de la transition. Pour alléger, nous notons par un point le fait que le jeton doit être conservé dans sa place lors de l'exécution d'une transition. L'absence de point permet de modéliser les mises à jour par les règles. La figure XV.20 illustre le PrTN correspondant au programme de règles déjà modélisé figure XV.18 et figure XV.19.

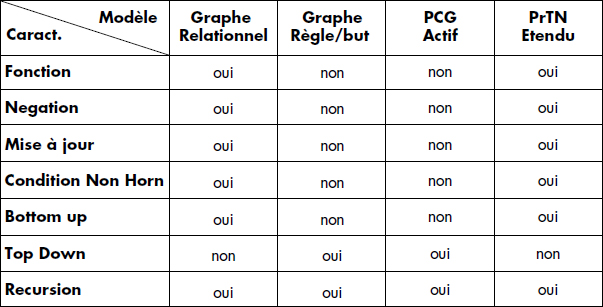
La figure XV.21 présente une synthèse des principales caractéristiques des différents modèles graphiques introduits ci-dessus. Notez que l'élément déterminant apparaît finalement être l'orientation top-down (dirigée par les questions) ou bottom-up (dirigée par les données) du modèle. Différentes variantes de ces modèles ont aussi été proposées ; elles permettent en général de mieux prendre en compte une fonctionnalité du langage de règles modélisé.

Le problème de l'optimisation et de l'évaluation de requêtes portant sur des prédicats dérivés récursifs est étudié depuis longtemps [Gallaire78, Minker82]. Il s'agit d'un problème difficile et important compte tenu de l'influence de la récursion, notamment dans les applications d'intelligence artificielle. [Bancilhon86b] expose les premières solutions connues.

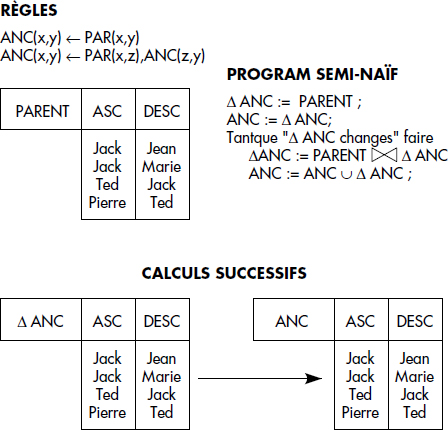
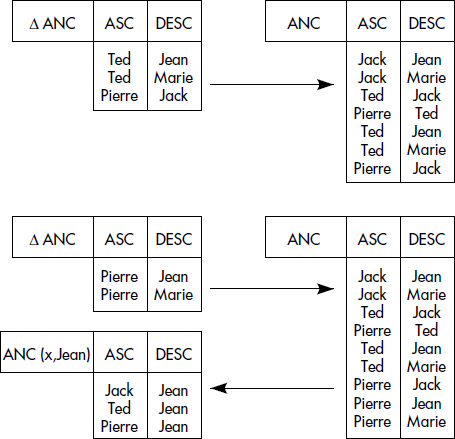
Un exemple typique, déjà vu ci-dessus, de prédicat dérivé récursif est la définition des ancêtres ANC à partir d'une relation de base parent notée PAR(PARENT,ENFANT) comme suit :

• (r1) ANC(x,y) ← PAR(x,y)
• (r2) ANC(x,y) ← PAR(x,z), ANC(z,y)

Un tel exemple est linéaire, car la relation ANC est définie en fonction d'une seule occurrence de la relation ANC dans la seule règle récursive (r2). Il est possible de donner une définition non linéaire des ancêtres en remplaçant la règle r2 par :

• ANC(x,y) ← ANC(x,z),ANC(z,y)

Cette règle est quadratique, car ANC apparaît deux fois dans le corps.

Un exemple typique est celui du calcul des cousins de même génération. Pour initialiser la relation MG(PERSONNE,PERSONNE) définissant les cousins de même génération, il est commode de constater que chacun est son propre cousin de même génération. Toutes les personnes connues étant stockées dans une relation unaire HUM (humains), on obtient la règle d'initialisation :

• (r1)      MG(x,x) ← HUM(x)

Notez que la relation humain (HUM) peut être obtenue par les deux règles :

• HUM(x) ← PAR(x,y)
• HUM(y) ← PAR(x,y)

Pour compléter la relation MG, on dira qu'une personne x est le cousin de même génération qu'une personne y si deux de leurs parents sont aussi cousins de même génération. On aboutit alors à la règle :

• (r'2) MG(x,y) ← PAR(xp,x),MG(xp,yp),PAR(yp,y)

Il existe plusieurs autres manières de définir les cousins de même génération. En particulier, comme MG est une relation symétrique (MG(x,y) ⇔ MG(y,x)), il est possible d'intervertir les variables xp et yp à l'intérieur de MG dans r2. Cela conduit à la définition suivante des cousins de même génération :

• (r1) MG(x,x) ← HUM(x)
• (r2) MG(x,y) ← PAR(xp,x),MG(yp,xp),PAR(yp,y)

Un exemple plus complexe, car quadratique, est la définition des personnes au même niveau hiérarchique par un prédicat déduit MC(EMPLOYE,EMPLOYE), spécifiée à partir d'une relation SER(SERVICE,EMPLOYE) et d'une relation CHEF(EMPLOYE,EMPLOYE) :

• (r1) MSER(x,y) ← SER(s,x),SER(s,y)
• (r2) MC(x,y) ← MSER(x,y)
• (r3) MC(x,y) ← CHEF(x,z1),MC(z1,z2),MSER(z2,z3),MC(z3,z4),CHEF(y,z4)

Cet exemple est quadratique, car la règle récursive r3 définit le prédicat dérivé MC en fonction de deux occurrences du même prédicat. Elle est illustrée figure XV.22. Il est évidemment possible de définir la relation MC de manière plus simple, la complexité ayant ici pour but de mieux illustrer dans des cas non triviaux les différents algorithmes que nous verrons ci-dessous.

Il est aussi possible d'utiliser DATALOG^fonc afin de définir des prédicats récursifs avec calculs de fonctions. Des exemples typiques sont dérivés des problèmes de parcours de graphes. Un graphe valué peut être représenté par une relation :

• ARC (SOURCE, CIBLE, VALUATION)

Chaque tuple de la relation représente un arc. Les règles suivantes déduisent une relation CHEMIN représentant tous les chemins du graphe, avec une valuation composée calculée par une fonction f :

• CHEMIN(x,y,z) ← ARC(x,y,z)
• CHEMIN(x,y,f(z1,z2)) ← ARC(x,z,z1), CHEMIN(z,y,z2)

Par exemple, si f(z1,z2) = z1 + z2 et si les valuations représentent des distances, les règles précédentes définissent tous les chemins du graphe avec leur longueur associée.

Une autre application possible des fonctions dans les règles récursives est la manipulation d'objets structurés. Par exemple, des listes peuvent être manipulées avec la fonction concaténation de deux listes X et Y, notée X|Y. La base de données peut être composée d'un prédicat définissant l'ensemble des listes constructibles à partir de n éléments. On spécifie l'ajout (par la fin) d'une liste X à une liste Y comme étant une liste Z définie par le prédicat AJOUT(X,Y,Z), puis l'inversion des éléments d'une liste X comme étant une liste Y définie par le prédicat INVERSE(X,Y). Les règles suivantes définissent ces prédicats dérivés ([] désigne la liste vide) :

• (r1) AJOUT(X,[],X|[]) ← LISTE(X)
• (r2) AJOUT(X,W|Y,W|Z) ← AJOUT(X,Y,Z),LISTE(W)
• (r3) INVERSE([],[]) ←
• (r4) INVERSE(W|X,Y) ← INVERSE(X,Z),AJOUT(W,Z,Y)

AJOUT et INVERSE sont ainsi deux prédicats récursifs linéaires.

Le problème qui se pose est bien sûr d'évaluer des questions portant sur des prédicats récursifs. Ces questions spécifient en général des constantes pour certaines variables, ou des ensembles de constantes (question avec ≤, <, ≥, >). Voici quelques questions typiques sur les prédicats définis précédemment :

• (1) Qui sont les ancêtres de Jean ?
      ? ANC(x,Jean)
• (2) Pierre est-il un ancêtre de Jean ?
      ? ANC(Pierre,Jean)
• (3) Qui sont les cousins de même génération de Jean ?
      ? MG(Jean,x)
• (4) Qui sont les chefs au même niveau que Jean ?
      ? MC(Jean,x)
• (5) Quel est l'inverse de la liste [1,2,3,4,5] :
      ? INVERSE([1,2,3,4,5], x)

Il est bien sûr possible de remplacer par des constantes tout sous-ensemble de paramètres afin de retrouver les autres (cependant, selon les instanciations, DATALOG^fonc peut conduire à des réponses infinies comme vues ci-dessus), ou encore d'instancier tous les paramètres afin d'obtenir une réponse booléenne du type VRAI/FAUX.

Dans la suite, nous allons étudier les principales solutions proposées, en commençant par les solutions simples, en général peu performantes ou incomplètes. Nous étudierons ensuite les solutions interprétées qui transforment progressivement la requête en sous-requêtes adressées au SGBD, puis les solutions compilées qui, dans un premier temps, génèrent un programme d'algèbre relationnelle et dans un deuxième temps demandent l'exécution de ce programme. Bien que décrivant les principales approches, notre étude est loin d'être complète. En particulier, nous ignorons des approches importantes basées sur des règles de réécriture [Chang81], des automates ou une méthode de résolution adaptée [Henschen84].

XX-7-2-1. La génération naïve▲

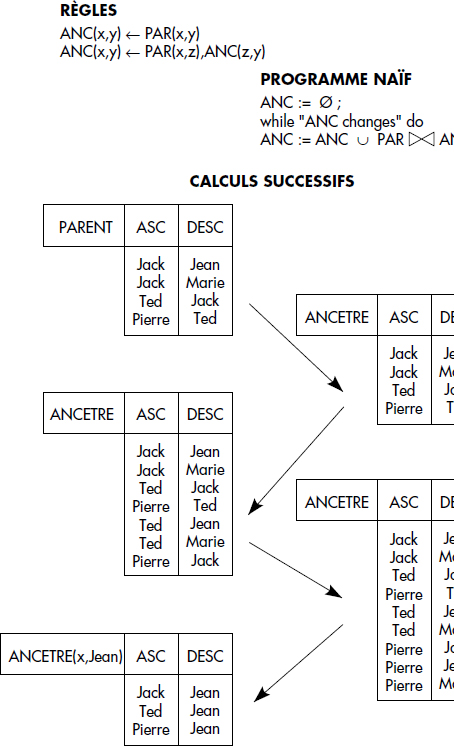
La solution la plus naïve pour évaluer la réponse à une requête consiste simplement dans un premier temps à appliquer un chaînage avant direct à partir des prédicats de base jusqu'à saturation des prédicats dérivés. Dans un deuxième temps, une sélection sur les prédicats dérivés instanciés permet de retenir les tuples répondant à la question. Cette solution est connue sous le nom de génération naïve.

Notion XV.22 : Génération naïve (Naïve Generation)

Technique d'évaluation bottom-up calculant une relation déduite par application de toutes les règles à tous les tuples produits à chaque étape du processus de génération, jusqu'à saturation de la relation déduite.

Cette méthode de calcul de point fixe part donc des faits de la base et calcule les instances des prédicats dérivés par application des règles afin de répondre à la question. En général, une valeur R₀ est calculée pour le prédicat récursif à partir des règles d'initialisation. Puis, par un programme de l'algèbre relationnelle qui résulte d'une compilation élémentaire de la règle récursive, on effectue un calcul itératif R = R ∪ E(R), où E est l'expression de l'algèbre relationnelle traduisant la règle récursive. Le processus s'arrête quand l'application de E à R ne permet pas de générer de nouveau tuple : on a alors le point fixe du prédicat récursif défini par R = E(R). Ce point fixe existe en DATALOG [Aho-Ullman79]. Un programme de calcul naïf d'une relation récursive R s'écrit donc comme représenté figure XV.23, E étant une expression de l'algèbre relationnelle dérivée de la règle récursive.

Figure XV.23 : Programme de génération naïve

Sélectionnez

Procedure Naïve (R) {
    R:4= R0 ;
    Tant que « R change » Faire
        R := R ∪ E(R) ;
}

Par exemple, dans le cas des ancêtres, on initialisera ANC par la règle r1 avec les parents, puis on appliquera la règle r2 en effectuant une boucle de jointures de la relation ANC avec la relation PAR, et ce jusqu'à ce que l'on ne génère plus de nouvel ancêtre. Le calcul est illustré figure XV.24. Le processus sera similaire pour générer la relation MC : les règles r1 et r2 permettent de lui attribuer une valeur initiale MC0, puis les jointures des relations CHEF, MC0,MSER, MC0,CHEF permettront de calculer MC1. De manière itérative, les jointures de CHEF, MCi, MSER, MC_i, CHEF permettront de calculer MCi+1. Le calcul s'arrêtera quand aucun nouveau tuple ne sera généré : on aura obtenu le point fixe de la relation MC qui décrit toutes les personnes de la base à un même niveau hiérarchique.

Si les programmes de règles sont en DATALOG pur, comme pour ANC et MC, il n'existe pas de fonction pour générer des valeurs qui ne sont pas dans la base : ceci garantit la finitude du processus de génération [Aho-Ullman79]. Dans le cas des listes, la stratégie bottom-up ne peut être appliquée telle quelle ; en effet, par ajout de listes, on génère des listes sans fin. Le processus de génération ne se termine pas.

Une étude plus détaillée du processus de génération naïf démontre plusieurs faiblesses de la méthode, outre le fait qu'une terminaison n'est garantie qu'en cas d'absence de fonction :

1. À chaque itération, un travail redondant est effectué, qui consiste à refaire les inférences de l'itération précédente ; cela provient du fait que l'on cumule les résultats avec les anciens et que l'on applique à nouveau la jointure à tous les résultats sans distinction.
2. Dans le cas où des constantes figurent dans la question, un travail inutile est effectué, car la génération produit des résultats qui ne figurent pas dans la réponse ; ils sont éliminés par la sélection finale. Par exemple, pour calculer les seuls ancêtres de Jean, le processus conduit à générer les ancêtres de toutes les personnes de la base.

Voici maintenant les principales méthodes qui répondent à ces critiques.

XX-7-2-2. La génération semi-naïve▲

CHEF  ∆MCi  MSER  MCi  CHEF
CHEF  MCi  MSER  ∆MCi  CHEF
CHEF  ∆MCi  MSER  ∆MCi  CHEF

Procedure SemiNaïve (R) {
    ∆R := R0 ;
    R := ∆R ;
    Tant que ∆R ≠ Ø faire {
        ∆R = ∆E(R, ∆R) ;
        ∆R = ∆R - R ;
        R = R ∪ ∆R ;
    }
}

XX-7-3-1. Approches et difficultés▲

Au lieu d'appliquer le chaînage avant pour générer la réponse à une question, il est possible de travailler en chaînage arrière « à la PROLOG ». Une telle approche part de la question pour remonter aux faits via les règles. En conséquence, elle est qualifiée de stratégie top-down comme vu ci-dessus. Malheureusement, dans le cas de règles récursives la méthode top-down peut conduire à boucler.

Nous allons tout d'abord montrer une application de la méthode dans le cas favorable. Par exemple, avec la règle :

 

Sélectionnez

ANC(x,y) ← PAR(x,z), ANC(z,y)

la question ANC(Jean,y) génère la sous-question PAR(Jean,z),ANC(z,y). Tenter de résoudre directement ANC(z,y) en chaînage arrière conduit à boucler. Par contre, si l'on évalue PAR(Jean,z) sur la relation de base PARENT, on obtient des constantes c0, c1… pour z. Il devient alors possible de résoudre en chaînage arrière ANC(c0,y),ANC(c1,y)… qui génèrent les sous-questions PAR(c0,z),ANC(z,y),PAR(c1,z),ANC(z,y), etc. Le processus s'arrête quand il n'existe plus de sous-question générable du type PAR(ci,z) ayant une réponse non vide.

La méthode n'est cependant applicable que dans le cas particulier où la constante de la question se propage pour regénérer la même sous-question. Par exemple, dans le cas de la règle :

 

Sélectionnez

ANC(x,y) ← ANC(x,z), PAR(z,y)

la question ANC(Jean,y) conduit à générer la sous-question ANC(Jean,z). Changer y en z ne fait pas progresser le problème et le processus boucle totalement. Nous verrons dans la suite des extensions de cette approche « à la PROLOG » qui permettent d'éviter le bouclage en utilisant les autres règles et en mêlant chaînage arrière-chaînage avant. Auparavant, nous allons étudier plus en détail la propagation des constantes dans les règles.

XX-7-3-2. La remontée d'informations via les règles▲

Quand elles s'appliquent, les méthodes par chaînage arrière remontent les constantes depuis la question vers les relations de base et permettent donc d'effectuer les restrictions avant la récursion. Afin de mieux comprendre la remontée des constantes dans le corps des règles, il est possible de l'illustrer par un graphe appelé graphe de propagation. Il s'agit là d'une représentation des propagations d'informations entre prédicats au sein d'une règle [Beeri87], appelées en anglais Sideways Information Passing [Ullman86].

Notion XV.24 : Propagation d'informations (Information Passing)

Passage de constantes instanciant une variable x d'un prédicat P(…,x…y…) à un autre prédicat Q(…,y…) en effectuant une sélection sur P avec les valeurs de x, suivie d'une jointure avec Q sur y.

Les propagations d'informations dans les règles se représentent donc par des graphes. Un graphe de propagation pour une règle est un graphe étiqueté qui décrit comment les constantes obtenues par la tête de la règle se propagent aux autres prédicats de la règle. Il existe plusieurs graphes de propagation possibles pour une règle, suivant les choix de propagation effectués. Pour faciliter la compréhension et éviter de répéter des morceaux de règles, une représentation simplifiée avec des bulles représentant les sommets du graphe est proposée. Les prédicats de la règle sont écrits de gauche à droite, depuis la tête jusqu'au dernier prédicat de la condition. Un sommet du graphe (donc représenté par une bulle) est soit un groupe de prédicats, soit un prédicat récursif. Un arc N → p relie un groupe de prédicats N à une occurrence d'un prédicat récursif p. L'arc N → p est étiqueté par des variables dont chacune apparaît dans un prédicat de N et dans p. Un graphe de propagation est valide s'il existe un ordre des sommets (appelé ici ordre de validité) tel que, pour chaque arc, tout membre de sa source apparaisse avant sa cible. Pour faciliter la visualisation d'un graphe de propagation valide, il est souhaitable d'écrire les occurrences de prédicats selon l'ordre de validité. Les figures XV.27 et XV.28 présentent deux graphes de propagation valides pour les règles récursives des exemples Ancêtres et Chefs.

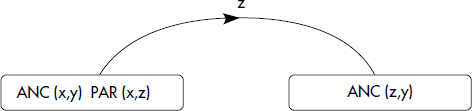
La signification intuitive d'un graphe de propagation valide est la suivante : en supposant instanciée la jointure des prédicats entourés par une bulle source d'un arc, il serait possible de propager les valeurs des variables étiquettes vers le prédicat cible de l'arc. Si la bulle source contient le prédicat de tête de la règle, un arc modélise la propagation de constantes vers un prédicat récursif en chaînage arrière suite à une instanciation d'une variable de la tête. Une telle propagation est donc une propagation par effet de bord.

Un graphe de propagation valide est linéaire si pour tout arc N → p, N contient tous les nœuds qui précédent p selon l'ordre de validité. Suivant [Beeri87], nous dirons qu'un graphe de propagation valide linéaire est total si toute variable d'un prédicat récursif r cible d'un arc apparaissant dans un prédicat qui précède r étiquette un arc entrant dans r. Nous utiliserons les graphes de propagation de constantes dans la suite, notamment pour la méthode des ensembles magiques généralisés [Beeri87].

XX-7-3-3. Les règles signées▲

ANC10(x,y) ← PAR(x,z), ANC10(z,y)
MC10(x,y) ← CHEF(x,z1),MC10(z1,z2),MSER(z2,z3),
MC10(z3,z4),CHEF(y,z4)

Les méthodes interprétées sont des extensions des méthodes de chaînage arrière « à la Prolog » qui traitent correctement les règles récursives, d'une part en utilisant bien les règles d'initialisation et d'autre part en incluant un tantinet de chaînage avant pour générer des sous-questions. Elles sont caractérisées par le fait qu'elles sont appliquées lors de l'exécution d'une question et non pas lors de l'entrée des règles, à la compilation.

L'approche QSQ (Query Sub-Query) décrite dans [Vieille86] a été implantée à l'ECRC (Munich). Elle est devenue QoSaQ lorsqu'elle a été généralisée au support complet de DATALOG. Elle peut être vue comme une amélioration de la méthode de chaînage arrière consistant à mémoriser les sous-questions générées lors de l'unification et à appliquer globalement les sous-questions de même forme, afin de limiter le nombre de sous-questions à traiter. Un ensemble de sous-questions { ? R(ai,y) | i ∈[1,n] } est ainsi remplacé par une seule sous-question avec critère disjonctif ? R({a1 a2 ∨…∨ an},y). La remontée des constantes pour déterminer les faits relevants s'effectue par chaînage arrière comme en PROLOG. De plus, une sous-question n'est exécutée que si elle ne l'a pas déjà été. Le critère d'arrêt est donc double : pas de nouvelle sous-question générée ou pas de nouveau fait relevant généré.

Ces techniques de mémorisation conduisent à une méthode rapide en temps d'exécution, mais relativement consommatrice en mémoire puisque faits relevants et sous-questions doivent être mémorisés. Deux versions de la méthode ont été implantées, l'une itérative qui parcourt la liste des sous-questions à traiter, l'autre récursive qui se rappelle à chaque sous-question avec critère disjonctif généré. Notez que la méthode QoSaQ résout les problèmes de cycles dans les données (par exemple, une personne qui serait son propre ancêtre) puisqu'elle n'exécute que des sous-questions nouvelles.

La méthode des ensembles magiques est une méthode compilée permettant de générer un programme d'algèbre relationnel étendu avec des boucles. Elle se compose d'une phase de réécriture des règles puis d'une seconde phase appliquant la génération semi-naïve vue ci-dessus. Elle est basée sur l'idée d'un petit génie [Bancilhon86a][Bancilhon86a] qui, avant application du chaînage avant semi-naïf, marque les tuples utiles du prédicat récursif R à l'aide d'un prédicat associé, appelé magique et noté MAGIQUE_R. Ainsi, les calculs en chaînage avant ne sont effectués que pour les tuples susceptibles de générer des réponses, qui sont marqués par le prédicat magique. La première version des ensembles magiques ne s'appliquait guère qu'aux règles récursives linéaires. Une version généralisée a été publiée sous le nom « d'ensembles magiques généralisés » [Beeri87]. Nous allons présenter maintenant cette version.

Le point de départ est un programme de règles signées comme vu ci-dessus et un graphe SIP de propagation de constantes par effets de bord. L'intention est de générer un programme de règles qui, à l'aide du ou des prédicats magiques, modélise le passage des informations entre prédicats selon le graphe SIP choisi. Pour chaque prédicat récursif signé R^xx, un prédicat magique est créé, noté MAGIQUE_R^xx dont les variables sont celles liées dans R^xx ; l'arité du prédicat MAGIQUE_R^xx est donc le nombre de bits à 0 dans la signature xx. Ainsi, un prédicat magique contiendra des constantes qui permettront de marquer les tuples de R^xx utiles. Chaque règle est modifiée par addition des prédicats magiques à sa partie condition, pour restreindre l'inférence aux tuples marqués par les prédicats magiques. Par exemple, une règle :

B1xx,B2xx…R10,C1xx,C2xx… → R10(x,y)

sera transformée en :

MAGIC_R10(x), B1xx,B2xx…R10,C1xx,C2xx… → R10(x,y)

qui signifie que la condition ne doit être exécutée que pour les tuples de R¹⁰ marqués par le prédicat MAGIC_R¹⁰(x).

Le problème un peu plus compliqué à résoudre est de générer les constantes du (ou des) prédicat(s) magique(s) pour marquer tous les tuples utiles et, si possible, seulement ceux-là. Une première constante est connue pour un prédicat magique : celle dérivée de la question ; par exemple, avec la question ? R(a,x), on initialisera le processus de génération des prédicats magiques par MAGIC_R¹⁰(a). La génération des autres tuples du (ou des) prédicat(s) magique(s) s'effectue en modélisant les transmissions de constantes à tous les prédicats dérivés par le graphe SIP choisi. Plus précisément, pour chaque occurrence de prédicat dérivé R^xx apparaissant dans le corps d'une règle, on génère une règle magique définissant les variables liées de R^xx comme suit : la conclusion de la règle est MAGIQUE_R^xx(…) et la condition est composée de tous les prédicats qui précédent R^xx dans le graphe SIP, les prédicats dérivés dont certaines variables sont liées étant remplacés par les prédicats magiques correspondants. Les variables sont déterminées par le graphe SIP et par les bits à 1 des signatures pour les prédicats magiques. Vous trouverez une explication plus détaillée et une preuve partielle de la méthode dans [Beeri87].

Nous traitons les exemples des ancêtres et des mêmes chefs avec la méthode des ensembles magiques généralisés figure XV.29. Les résultats montrent que les règles de production générées répètent pour partie la condition de la règle précédente. Ce n'est pas optimal, car on est conduit à réévaluer des conditions complexes. Une solution consistant à mémoriser des prédicats intermédiaires de continuation a été proposée sous le nom d'« ensembles magiques généralisés supplémentaires » [Beeri87]. Cette méthode est voisine de celle d'Alexandre proposée par ailleurs [Rohmer86]. Pour le cas des règles linéaires, une version améliorée des ensembles magiques a aussi été proposée [Naughton89]. Le mérite de la méthode reste cependant la généralité.

XX-7-6-1. La méthode fonctionnelle▲

Les deux méthodes présentées précédemment conduisent à réécrire un programme de règles avec des prédicats problèmes ou magiques, pour pouvoir l'exécuter de manière optimisée en chaînage avant semi-naïf. Malheureusement, le programme de règles obtenu est en général complexe (plus de règles que le programme initial, récursion mutuelle) et l'exécution semi-naïve peut être lourde. Par exemple, dans le cas des ancêtres, la question ?ANC(Jean,y) conduit à trois règles vues ci-dessus, alors que la solution consiste simplement à calculer la fermeture transitive de la relation parent à partir de Jean. Ces remarques, avec en plus le fait que la démonstration de la complétude des méthodes précédentes est complexe, nous ont conduits à développer une méthode plus formelle basée sur des équations au point fixe qui s'applique dans un contexte général avec fonctions [Gardarin87].

Une méthode d'évaluation simple qui découle de la sémantique de DATALOG consiste à écrire des équations au point fixe en algèbre relationnelle. Malheureusement, la propagation directe des constantes n'est pas possible dans de telles équations dès que celles-ci se reportent sur une condition de jointure. Afin de modéliser dans les équations au point fixe la propagation des constantes, nous utilisons des fonctions à arguments ensemblistes. L'idée intuitive de la méthode est qu'une instance de relation définit en fait des fonctions ; chaque fonction transforme un ensemble de valeurs d'une colonne dans l'ensemble de valeurs correspondant dans une autre colonne. Ainsi, toute question ? R(a,y) est interprétée comme une fonction r appliquant l'ensemble des parties du domaine de a dans l'ensemble des parties du domaine de y, c'est-à-dire avec des notations classiques, r : 2^dom(^a) → 2^dom(y). Évaluer la question ? R(a,y) revient alors à évaluer la fonction r({a}).

Étant donnés une question et un ensemble de règles, un algorithme permet de générer une équation fonctionnelle au point fixe du type r = F(r), où F est une expression fonctionnelle. Pour ce faire, des opérations monotones entre fonctions ont été introduites :

1. La composition de deux fonctions f o g (X) = f(g(X)) modélise en fait une jointure suivie d'une projection ;
2. L'addition (f+g) (X) = f(X) ∪ g(X) modélise l'union ;
3. L'intersection (f ∩ g) (X) = f(X) ∩ g(X) permet de modéliser des jointures cycliques.

Dans le cas de règles à prédicats binaires sans fonction, l'algorithme est simple et repose sur un graphe de connexion des variables dans la règle. Ce graphe représente simplement par un nœud chaque variable et par un arc les prédicats (ou un hyper arc dans le cas de prédicats non binaires). Il est orienté pour visualiser les passages d'information en chaînage arrière. Ce graphe peut être perçu comme une simplification du graphe de propagation d'information vu ci-dessus.

La génération d'équation fonctionnelle s'effectue par un algorithme de cheminement dans le graphe, chaque arc étant interprété comme une fonction de calcul du nœud cible en fonction du nœud source. Cet algorithme décrit dans [Gardarin86] est appliqué ci-dessous aux cas des ancêtres et des chefs. Pour simplifier les notations, pour toute relation binaire R(x,y), R(X) dénote la fonction qui applique {x} sur {y} et R'(Y) celle qui applique {y} sur {x}. Après obtention, l'équation fonctionnelle au point fixe est simplement résolue par application du théorème de Tarski [Tarski55].

Nous illustrons tout d'abord la méthode avec le problème des ancêtres. La figure XV.30 représente les graphes de connexion des variables des règles :

 

Sélectionnez

ANC(x,y) ← PAR(x,y)
ANC(x,y) ← PAR(x,z),ANC(z,y)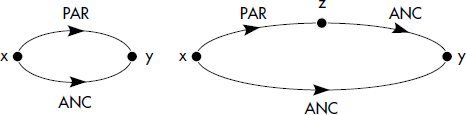

L'équation fonctionnelle au point fixe résultante est :

 

Sélectionnez

ANC(X) = PAR(X) + ANC(PAR(X))

En appliquant le théorème de Tarski à cette équation, la solution obtenue est :

 

Sélectionnez

ANC(X) = PAR(X) + PAR(PAR(X)) +… + PAR(PAR(PAR…(PAR(X))))

qui peut être traduite directement en algèbre relationnelle par un retour aux notations classiques (nous supposons ici la relation ANC acyclique ; une hypothèse contraire nécessite d'élaborer le test d'arrêt). Le programme résultant (figure XV.31) calcule ainsi les ancêtres d'un ensemble de personnes X dans ANC.

Figure XV.31 : Calcul des ancêtres de X

Sélectionnez

PROCEDURE CALCUL(ANC,X); {
    ANC := Ø;
    DELTA := X;
    Tant que DELTA ≠ Ø faire {
        DELTA := ????PAR.2 (σPAR.1∈DELTA (PAR));
        ANC := ANC ∪ DELTA;
    }
}

De manière plus générale, la méthode s'applique très simplement aux règles fortement linéaires de la forme :

 

Sélectionnez

R(X,Y) ← B1(X,Y)
R(X,Y) ← B2(X,X1),R(X1,Y1),B3(Y1,Y)

où B1, B2 et B3 sont des relations de base ou simplement des jointures/restrictions de relations de base et où X, Y, X1, Y1 représentent des variables ou des n-uplets de variables. Le graphe de connexion des variables de ce type de règles est représenté figure XV.32.

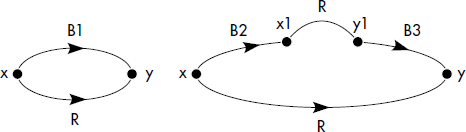
L'équation fonctionnelle au point fixe est, pour des questions du type ? R(a,Y) :

 

Sélectionnez

r(X) = b1(X) + b3(r(b2(X)))

Le théorème de Tarski permet d'obtenir la forme générale de la solution :

 

Sélectionnez

r(X) = b1(X) + b3(b1(b2(X))) +… + b3n(b1(b2n(X)))

Le calcul de ce polynôme est effectué par le programme de l'algèbre relationnelle optimisé suivant dont la terminaison suppose l'acyclicité des données de la relation B2 (sinon, il faut ajouter une différence). Pour obtenir la réponse à une question du type ? R(a,Y), il suffit de remplacer X par a dans le programme de la figure XV.33. Celui-ci est utilisable quand X est instancié par un ensemble de valeurs.

Figure XV.33 : Calcul des réponses à des requêtes sur règles fortement linéaires

Sélectionnez

PROCEDURE CALCUL(R,X); {
    i,n : integer;
    n:= 0 ;
    R := ????B1.2 (σB1.1 ∈ X(B1));
    B2N := X;
    Tant que B2N ≠ Ø faire {
        n := n + 1;
        B2N := ????B2.2 (σB2.1 ∈ B2N(B2));
        DELTA := ????B1.2 (σB1.1 ∈ B2N(B1));
        Pour i : = 1 à n faire {
            DELTA := ????B3.2 (σB3.1 ∈ B2N(B3));
            R := R ∪ DELTA;
        }
    }
}

XX-7-6-2. Les méthodes par comptages▲

R(X,Y) ← B1(X,Y)
R(X,Y) ← B2(X,X1),R(X1,Y1),B3(Y1,Y)

COMPTE(0,a)
COMPTE_B2(J,X), B2(X,X1) → COMPTE_B2(J+1,X1)
COMPTE_B2(J, X), B1(X,Y) → DECOMPTE_B3(J,Y)
DECOMPTE_B3(J,Y1),B3(Y1,Y) → DECOMPTE_B3(J-1,Y)
DECOMPTE_B3(0,Y) → R(Y)

XX-7-6-3. Les opérateurs graphes▲

Afin d'illustrer la problématique, nous introduisons ici le langage ROL (Rule Object Language) prototypé au laboratoire PriSM au début des années 1990 [Gardarin94]. ROL s'appuie sur le modèle objet de C++. Un schéma de bases de données est défini par une description dans un langage analogue à ODL de l'ODMG. La figure XV.34 illustre un schéma ROL. Celui-ci est directement implémenté en C++. Pour les calculs intermédiaires, il est possible de définir des classes temporaires par le mot-clé TRANSIENT.

CLASS Point { Float Abs ; Float Ord ;} ;
CLASS Personne {String Nom; String Prénom;
    LIST<Point> Caricature; };
CLASS Acteur : Personne { Real Salaire;
    Real Augmenter (Real Montant) ; };
CLASS Film {Int Numf; String Titre; SET<String> Categories;
    Relationship Set<Acteur> Joue ;};
CLASS Domine { Int Numf; Acteur Gagnant; Acteur Perdant; };
TRANSIENT CLASS Calcul { } ;

Les règles en ROL sont organisées en modules. Chaque module commence par des définitions de variables valables pour tout le module, de la forme :

VAR <nom> IN <collection>

Le nom d'une variable est généralement une lettre, alors qu'une collection est une extension de classe ou une collection dépendantes, comme en OQL. Il est aussi possible d'utiliser des variables symboliques (chaînes de caractères), afin d'améliorer la clarté des programmes. Nous définissons simplement les variables :

VAR X IN Film, VAR Y IN X.Categories ;
VAR Z IN Calcul ;

Les règles sont perçues comme des règles de production de la forme :

IF <condition > THEN <action>

La condition est analogue à une qualification de requêtes OQL. C'est une combinaison logique de conditions élémentaires. Une condition élémentaire permet de comparer deux termes. Un terme est une constante, un attribut, une expression de chemin ou de méthode. Les actions sont :

• Des insertions de valeurs. Une valeur éventuellement complexe (tuple par exemple) est insérée dans une collection temporaire ou persistante par la construction +<collection>(<valeurs>).
• Des créations d'objets. Un objet est créé dans une collection temporaire ou persistante par la construction +<classe>(<paramètres>). La classe doit être définie auparavant. L'action provoque simplement l'appel au constructeur d'objet avec les paramètres indiqués.
• Des destructions de valeurs. Une valeur d'une collection est détruite par la construction -<collection>(<valeurs>).
• Des destructions d'objets. Un objet est détruit dans une collection temporaire ou persistante par la construction -<classe>(). La classe doit être définie auparavant. L'action provoque simplement l'appel au destructeur de l'objet avec les paramètres indiqués sur les objets de la classe sélectionnés par la condition.
• Des appels de méthodes. Toute méthode définie au niveau du schéma est valide en partie action précédée de + pour faciliter la lecture des expressions.
• Un bloc d'actions élémentaires (création et destruction d'objets et/ou valeurs, appels de méthodes). Une règle peut avoir en conséquence une suite d'actions séparées par des + et des -. Elle peut donc accomplir des mises à jour, des impressions, etc.

Une sémantique ensembliste type point fixe est donnée au langage par traduction en algèbre d'objet complexe [Gardarin94]. Les difficultés des langages objet est qu'ils intègrent à la fois la création de nouveaux objets (l'invention d'objets d'après [Abiteboul90]) et les fonctions. De ce fait, il est facile d'écrire des programmes infinis dès qu'on utilise des règles récursives. À notre connaissance, aucun compilateur n'est capable de détecter les programmes non sains.

À titre d'illustration, nous définissons figure XV.35 deux règles en ROL. La première réalise une suite d'actions pour tous les films d'aventure dans lesquels joue Quinn avec un salaire supérieur à 1 000 $ de l'heure. La seconde calcule la fermeture transitive de la relation Domine, puis imprime qui fut (transitivement) meilleur que Marilyn. Il n'y a pas de boucle infinie, car MEILLEUR est défini comme un ensemble. Il n'en serait rien avec une liste. Notons aussi que la structure de blocs imbriqués permet de définir des ordres de calcul, donc une certaine stratification. De tels langages sont complexes, mais puissants. Les perspectives d'applications sont importantes d'après [Nicolas97].

{ VAR F IN Film, A IN F.Joue, C IN F.Categorie ;
  IF A.Name='Quinn' AND A.salary≥1000 AND C='Aventure')
  THEN { +Calcul(F.Titre, F.Categories, A.Salaire)
       +F.Categories('cher')
       -F.categories('gratuit')
       +Print(F.titre, 'Mon cher Quinn') };

{ TRANSIENT SET Meilleur (Gagnant String, Perdant string);
  VAR Domine D, Meilleur B, C ;
  { IF EXISTS(D) THEN +Meilleur(D.Gagnant, D.Perdant);
    IF B.Perdant = C.Gagnant THEN
      +Meilleur(B.Gagnant, C.Perdant);}

IF B.Perdant.Nom ="Marilyn" THEN
      +Print(B.Gagnant, "fut meilleur que", B.Perdant); } ;

DEL est le langage supporté par le système Validity, commercialisé par la société Next Century Media [Next98]. DEL signifie Datalog Extended Language. DEL étend en effet DATALOG avec des objets typés, des prédicats prédéfinis (built-in), des quantificateurs et des ordres impératifs. L'ensemble est un langage déductif très puissant, permettant d'inférer sur de grandes bases d'objets.

Le modèle de données est un modèle objet. Les types DEL sont organisés selon une hiérarchie d'héritage. Ils sont atomiques ou composites. Les types composites comportent les collections classiques de l'objet (set, bag et list) et les tuples. Les types atomiques sont les booléens, les littéraux numériques (entiers et flottants), les chaînes de caractères et les références aux objets. Il est possible de définir des types utilisateurs en étendant la hiérarchie.

Les types peuvent être encapsulés dans des méthodes et fonctions écrites dans le langage impératif de DEL, en C ou en C++. Le langage impératif est un langage structuré par blocs, analogue aux langages classiques. Il est possible de calculer des expressions et d'effectuer des contrôles. Un ordre foreach est disponible pour parcourir les collections. Une collection peut être l'extension d'un prédicat dérivé par des règles.

Le langage de règles permet d'écrire des règles en DATALOG étendu avec des fonctions et des références. Les règles ne sont pas limitées aux clauses de Horn : il est possible d'utiliser des connecteurs logiques AND, OR et NOT, et des quantificateurs EXISTS et FORALL. En outre, le calcul de prédicats est étendu pour manipuler des identifiants d'objets, des opérations d'agrégats et des expressions de chemins limitées. Une tête de règle est un prédicat dérivé. DEL supporte les règles récursives.

Au-delà des corps de règles, les conditions permettent d'exprimer des contraintes d'intégrité et peuvent être utilisées dans les ordres impératifs conditionnels (if et while). DEL supporte aussi de nombreux prédicats prédéfinis appelables depuis les conditions ou les ordres impératifs. Le temps est également supporté sous différentes formes. DEL apparaît donc comme un langage très puissant, capable d'améliorer la productivité des développeurs d'applications intelligentes. L'implémentation du système déductif a été réalisée à Bull, à partir des travaux effectués à la fin des années 80 à l'ECRC à Munich. Un gérant spécifique d'objets avec des méthodes de reprise et de gestion des accès concurrents efficaces sert de support au moteur d'inférence qui applique un dérivé de la méthode QoSaQ vue ci-dessus.