XIX. OPTIMISATION DE REQUÊTES OBJET▲
XIX-1. INTRODUCTION▲
Une des fonctionnalités essentielles des systèmes objet ou objet-relationnels est la possibilité d'interroger la base à partir de requêtes non procédurales, exprimées en OQL ou en SQL3 (voir chapitre précédent). Ces requêtes peuvent invoquer des opérations sur des types de données utilisateur. En effet, dans les SGBD objet ou objet-relationnels, l'utilisateur, ou plutôt un implémenteur système, peut ajouter ses propres types de données, avec des comparateurs logiques et des méthodes d'accès spécifiques. L'optimiseur doit alors être extensible, c'est-à-dire capable de supporter une base de règles de connaissances pouvant être étendue par l'utilisateur afin d'explorer un espace de recherche plus riche pour les plans d'exécution.
Un premier problème est d'être capable de générer tous les plans d'exécution possibles pour une requête complexe. Ceci nécessite tout d'abord des techniques de réécriture de requêtes en requêtes équivalentes. La réécriture peut s'effectuer au niveau de la requête source ; plus souvent, elle s'applique sur des requêtes traduites en format interne, sous forme d'arbres algébriques. De nombreux travaux ont été effectués sur les techniques de réécriture de requêtes objet [Graefe93, Haas89, Cluet92, Mitchell93, Finance94, Florescu96].
Un deuxième problème est le choix des algorithmes et méthodes d'accès les plus performants pour réaliser une opération de l'algèbre d'objets. Ce choix est plus riche que dans le cas relationnel pour les jointures qui peuvent maintenant s'effectuer directement par traversées de pointeurs. Le support direct de pointeurs sous forme d'identifiants invariants est en effet une des fonctionnalités nouvelles des systèmes objet, permettant la navigation. Le choix des algorithmes d'accès va dépendre du modèle de stockage qui inclut de nouvelles techniques d'indexation de chemins et de groupage d'objets. D'autres problèmes difficiles sont la mise en place d'opérateurs spécifiques sur collections et des index sur fonctions. Nous examinerons plus particulièrement les nouveaux algorithmes de traversées de chemins.
Comme dans le cas relationnel, le choix du meilleur plan nécessite un modèle de coût permettant d'estimer le coût d'un plan à la compilation. Ce modèle doit prendre en compte les groupages d'objets, les parcours de pointeurs, les index de chemins et aussi les méthodes utilisateur. Ceci pose des problèmes difficiles. Plusieurs modèles ont été proposés [Bertino92, Cluet92]. Nous en proposons un prenant en compte le groupage des objets.
Si l'on est capable de générer tous les plans candidats pour calculer la réponse à une requête et d'estimer le coût de chacun, il faut encore choisir le meilleur plan. Une stratégie exhaustive n'est pas possible compte tenu du grand nombre de plans en général. Des stratégies de recherche sophistiquées ont été proposées, depuis l'optimisation itérative [Ioannidis90, Lanzelotte91] jusqu'à la recherche génétique [Tang97]. Nous donnons dans ce chapitre une vue d'ensemble des méthodes aléatoires de recherche de plan optimal.
Ce chapitre présente une synthèse des techniques essentielles de l'optimisation des requêtes dans les bases de données objet, au-delà du relationnel. Il s'appuie en partie sur les travaux de recherche que nous avons menés au laboratoire PRiSM de Versailles de 1990 à 1996. Ces techniques commencent aujourd'hui à être intégrées dans les SGBD objet-relationnels et objet. Dans la section suivante, nous détaillons plus particulièrement la problématique d'optimisation spécifique à l'objet, en l'illustrant par quelques exemples. Dans la section 3, nous introduisons un modèle de stockage générique pour bases de données objet. La section 4 se consacre aux algorithmes de traversée de chemins. Nous donnons différents algorithmes de parcours d'associations et de collections imbriquées qui généralisent les algorithmes de jointures en cascade aux bases de données objet. La section 5 discute de la génération des plans équivalents et des types de règles de réécriture à considérer. Elle conduit à développer une architecture type pour un optimiseur extensible. La section 6 développe un modèle de coût pour SGBD objet. Nous examinons ensuite dans la section 7 les différentes stratégies de recherche du meilleur plan proposées par les chercheurs. Nous terminons le chapitre en proposant une stratégie génétique originale appliquée au choix d'algorithmes de traversées de chemins.
XIX-2. PROBLÉMATIQUE DES REQUÊTES OBJET▲
Dans cette section, nous examinons plus particulièrement les problèmes soulevés par l'optimisation de requêtes OQL ou SQL3 par rapport aux requêtes purement relationnelles, c'est-à-dire exprimées en SQL2.
XIX-2-1. QU'EST-CE QU'UNE REQUÊTE OBJET ?▲
Les bases de données objet et plus encore relationnel-objet permettent de formuler des requêtes classiques, c'est-à-dire exprimables en SQL de base. En conséquence, l'optimiseur d'un SGBD doit toujours être capable d'effectuer les optimisations étudiées pour le relationnel. Au-delà, les requêtes objet intègrent des constructions inexprimables en relationnel. À ce titre, elles posent des problèmes d'optimisation spécifiques. Les points nouveaux sont pour l'essentiel :
- Le support de méthodes et opérateurs définis par l'utilisateur. Dans les systèmes objet, l'utilisateur peut définir ses propres méthodes, ses propres comparateurs et aussi surcharger les opérateurs du langage de requêtes, par exemple l'addition. Ceci pose au moins trois problèmes d'optimisation : comment utiliser des accélérateurs, par exemple des index pour accélérer l'évaluation de requêtes ? Comment générer toutes les séquences de méthodes ou d'opérateurs possibles pour calculer la réponse à une requête ? Comment évaluer le coût d'une méthode programmée par l'utilisateur ?
- Les traversées de chemins. Celles-ci sont des extensions des jointures relationnelles effectuées directement par parcours de pointeurs. Ces pointeurs implémentent les associations. Il n'est pas toujours évident de les utiliser efficacement et parfois des jointures classiques peuvent être plus performantes.
- Les manipulations de collections. Les collections sont implémentées par des structures de données spécifiques et supportent des opérateurs spécifiques aux ensembles, par exemple union, intersection, différence, inclusion, recherche d'appartenance. Des règles de transformation nouvelles sont applicables aux collections. Il faut pouvoir en donner connaissance à l'optimiseur, qui doit être capable de les prendre en compte. De plus, évaluer le coût d'un opérateur sur collections n'est pas chose évidente.
- La prise en compte de l'héritage et du polymorphisme. L'héritage stipule que tout objet d'une sous-classe est membre implicite de la classe dont il hérite. Cette règle doit pouvoir être prise en compte lors de l'optimisation. Elle introduit des difficultés lors des surcharges ou redéfinitions de méthodes possibles grâce au polymorphisme dans les sous-classes. Les calculs de coût à la compilation des requêtes deviennent alors très difficiles, les méthodes réellement appliquées n'étant connues qu'à la compilation.
XIX-2-2. QUELQUES EXEMPLES MOTIVANTS▲
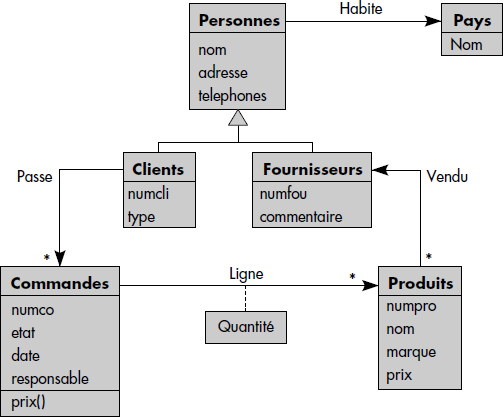
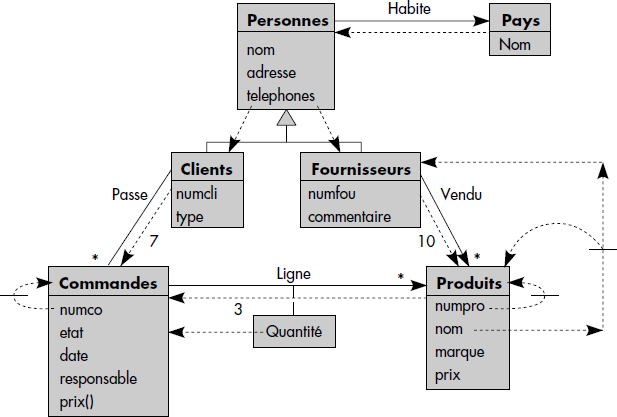
Nous illustrons le concept de requête objet par quelques exemples sur la base représentée figure XIV.1. Celle-ci est une interprétation objet de la situation bien connue où des clients passent des commandes de produits à des fournisseurs. Une commande contient plusieurs lignes. Clients et fournisseurs sont des personnes. Les chemins de traversée sont implémentés par des attributs portant le nom des associations contenant des identifiants d'objets. Ils sont marqués par des flèches.
XIX-2-2-1. Parcours de chemins▲
Supposons par exemple que l'on recherche le nom des produits et l'adresse des fournisseurs associés pour ceux de plus de 50 ans qui habitent en France. La question nécessite une expression de chemins en résultat, mais aussi deux expressions de chemins en qualification, pour tester les prédicats Age > 50 et Pays = "France". Elle peut s'écrire comme suit en OQL :
SELECT P.NOM, P.VENDU.ADRESSE
FROM PRODUITS P
WHERE P.PRIX > 10.000
AND P.VENDU.AGE > 50
AND P.VENDU.HABITE.PAYS = "FRANCE"On note que les chemins sont monovalués. Il est aussi possible de parcourir des chemins multivalués, en utilisant par exemple des collections dépendantes en OQL. La question suivante recherche par exemple les clients qui ont commandé des produits de prix supérieur à 10 000 :
SELECT C.NOM, C.ADRESSE
FROM CLIENTS C, C.PASSE M, M.LIGNE P
WHERE P.PRIX > 10.000Le problème essentiel pour ce type de requêtes est de choisir un algorithme de parcours des chemins de traversée, de sorte à réduire au maximum le nombre d'objets traversés. Des jointures par valeur, comme en relationnel, peuvent parfois être plus avantageuses afin de trouver rapidement des résultats à partir d'un petit nombre d'objets en mémoire.
XIX-2-2-2. Méthodes et opérateurs▲
Une partie de la base de données décrite figure XIV.1 peut être étendue avec la localisation géométrique des clients et des fournisseurs. Nous supposons que l'unité de mesure des distances est le kilomètre. Les types de données suivants peuvent être définis :
TYPE POINT (ATTRIBUTS X, Y COORDONNÉES ;
REAL FUNCTION DISTANCE(P1 POINT, P2 POINT));
TYPE ZONE (ATTRIBUTS P1, P2 POINT ;
BOOLEAN FUNCTION INCLUS(Z ZONE, P POINT));Considérons une implémentation des fournisseurs et clients par deux tables :
FOURNISSEURS (NUMFOU INT, NOM VARCHAR, ADR ADRESSE, NUMPAYS INT, TEL
TELEPHONES, LOCALISATION POINT);
CLIENTS (NUMCLI INT, NOM VARCHAR, ADR ADRESSE, NUMPAYS INT, TEL
TELEPHONE, LOCALISATION POINT);L'optimiseur doit alors être capable d'évoluer en prenant en compte les nouveaux types et les règles d'optimisation des opérations sur ces types. Par exemple, on pourra maintenant rechercher tous les fournisseurs localisés dans une zone donnée ( :Z) et à moins de 100 km d'un client donné ( :N) par la requête :
SELECT NUMFOU, NOM, ADRESSE
FROM CLIENTS C, FOURNISSEURS F
WHERE C.NUMCLI = :N AND INCLUS( :Z, F.LOCALISATION)
AND DISTANCE(C.LOCALISATION, F. LOCALISATION) < 100;Supposons maintenant que les types figure et cercle soient connus du SGBD extensible, défini comme suit :
TYPE FIGURE (ATTRIBUT CONTOUR LIST<POINT>;
BOOLEAN FUNCTION INCLUS (P POINT, F FIGURE))
TYPE CERCLE (ATTRIBUT CENTRE POINT, RAYON REAL;
CERCLE FUNCTION CERCLE(C POINT, R REAL);
FIGURE FUNCTION INTERSECTION(C CERCLE, Z ZONE));Une requête équivalente à la requête précédente consiste à chercher tous les fournisseurs inclus dans la figure géométrique résultant de l'intersection de la zone paramètre et d'un cercle de centre le client et de rayon 100 km, ce qui donne :
SELECT NUMFOU, NOM, ADRESSE
FROM CLIENTS C, FOURNISSEURS F
WHERE C.NUMCLI = :N
AND INCLUS(F.LOCALISATION, INTERSECTION(CERCLE(C.LOCALISATION,100),:Z)Un bon optimiseur doit être capable de déterminer le meilleur plan d'exécution pour cette requête. Il doit donc s'apercevoir de l'équivalence des formulations. Voilà qui n'est pas chose simple et demande de bonnes notions de géométrie !
XIX-2-2-3. Manipulation de collections▲
Outre les parcours de chemins vus ci-dessus, les collections peuvent être manipulées par des opérations spécifiques d'extraction de sous-collections, de concaténation, d'intersection, de recherche d'éléments, etc. Ces opérations peuvent obéir à des règles spécifiques de réécriture. Par exemple, trouver si un élément appartient à l'union de deux collections revient à trouver s'il appartient à l'une ou l'autre. Supposons que telephones soit un attribut contenant un ensemble de numéros de téléphone. La requête suivante recherche les nom et adresse des clients de Paris dont le numéro de téléphone est donné par la variable :N :
SELECT C.NOM, C.ADRESSE
FROM CLIENTS C
WHERE :N IN
UNION(SELECT S.TELEPHONES
FROM CLIENTS C
WHERE ADRESSE LIKE "PARIS")Grâce aux propriétés des ensembles, plus particulièrement de l'opérateur d'union par rapport à l'appartenance, elle doit pouvoir être transformée en une requête plus simple.
XIX-2-2-4. Héritage et polymorphisme▲
Lors d'une requête sur une superclasse, l'héritage nécessite de retrouver tous les éléments des sous-classes participant à la réponse. Couplé au polymorphisme, il peut impliquer des difficultés pour l'optimiseur. En effet, la liaison retardée conduit à ne pas connaître lors de la compilation le code réellement appliqué suite à un appel de méthode. Supposons une fonction revenus() calculant les revenus d'une personne. Celle-ci pourra être différente pour un fournisseur et un client, donc redéfinie au niveau de la classe clients et de la classe fournisseurs. La requête suivante :
SELECT NOM, ADRESSE
FROM PERSONNES
WHERE REVENUS() > 50.000nécessite donc a priori de calculer le revenu de chaque client et de chaque fournisseur pour vérifier s'il est supérieur à 50 000. La fonction effectivement appliquée dépend du sous-type de la personne. Le coût du plan est donc difficile à estimer lors de la compilation de la requête.
XIX-3. MODÈLE DE STOCKAGE POUR BD OBJET▲
Dans cette section, nous introduisons un modèle de stockage général pour bases de données objet. Ce modèle intègre différentes variantes d'identifiants d'objets, de techniques de groupage d'objets et d'indexation. Il est suffisamment général pour représenter les méthodes de stockage existant dans les SGBD. L'objectif est d'illustrer les techniques possibles, qui nous serviront plus loin de base aux calculs des coûts d'accès.
XIX-3-1. IDENTIFIANTS D'OBJETS▲
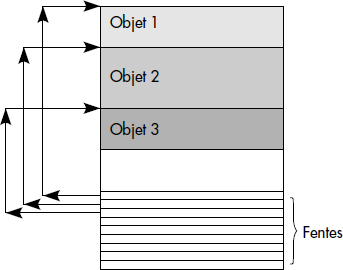
La plupart des SGBD stockent les objets dans des pages à fentes (slotted pages). Chaque page contient en fin de page un tableau de taille variable adressant les objets de la page. La figure XIV.2 illustre une page à fentes. Le déplacement conduisant du début de la page au début de chaque objet est conservé dans un petit index en fin de page.
Comme nous l'avons déjà vu, dans les SGBDO, les objets sont désignés par des identifiants d'objets. Il est possible de distinguer identifiants physiques et identifiants logiques.
Notion XIV.1 : Identifiant physique (Physical OID)
Identifiant d'objet composé d'un numéro de fichier, d'un numéro de page et d'un numéro de fente dans la page contenant l'objet.
Les identifiants physiques sont rapides à décoder pour atteindre l'objet référencé. Par contre, ils ne permettent pas le déplacement libre des objets dans la base. En cas de déplacement, une technique de chaînage doit être mise en place : l'entrée de la page initiale doit indiquer que l'objet n'est plus dans la page et pointe sur son nouvel identifiant physique. Cette technique de suite (forwarder) est très lourde à gérer, surtout si les objets se déplacent souvent. On lui préférera les identifiants logiques, plus coûteux lors de l'accès, mais invariants au déplacement d'objet.
Notion XIV.2 : Identifiant logique (Logical OID)
Identifiant d'objet composé d'un numéro d'entrée dans une table permettant de retrouver l'identifiant physique de l'objet.
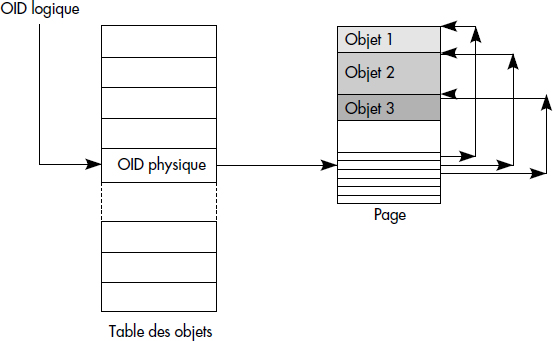
En cas de déplacement de l'objet, seule l'entrée dans la table est changée ; elle est positionnée à la nouvelle adresse de l'objet. En général, les SGBD gèrent une table d'identifiants logiques par type d'objets. La taille de la table est ainsi limitée. Pour la limiter plus encore et éviter les entrées inutiles, la table est souvent organisée comme une table hachée : chaque identifiant logique est affecté à une entrée déterminée par une fonction de hachage ; chaque entrée contient des couples de correspondance <identifiant logique-identifiant physique>. La figure XIV.3 illustre le décodage d'un identifiant logique.
Un bon modèle de stockage permet à la fois les identifiants physiques (OIDP) et les identifiants logiques (OIDL). Le choix du type d'identifiants affecte directement le coût de traversée des pointeurs.
XIX-3-2. INDEXATION DES COLLECTIONS D'OBJETS▲
Pour accélérer l'évaluation de requêtes avec prédicats de sélection, les systèmes offrent des index, généralement organisés comme des arbres-B contenant dans les feuilles des listes d'identifiants d'objets. Un index peut être perçu comme une fonction donnant une liste d'identifiants d'objets à partir d'une valeur d'attributs. Le coût de traversée d'un index est généralement de deux E/S, voire trois pour des très grosses collections d'objets.
Au-delà des index classiques, certains systèmes à objets offrent des index de chemins.
Notion XIV.3 : Index de chemin (Path index)
Index donnant pour chaque valeur d'un attribut d'une collection d'objets à l'extrémité d'un chemin tous les chemins menant à des objets ayant cette valeur d'attributs.
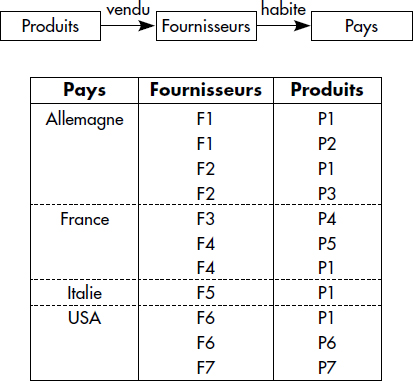
Il existe différents types d'index de chemins [Bertino89, Kim89]. Les index de chemin simples [Bertino89] [Kemper90] associent pour chaque valeur figurant à la fin du chemin tous les identifiants d'objets suffixes du chemin. Ils peuvent être implémentés comme des relations : chaque colonne d'un tuple correspond à une collection du chemin, en remontant depuis la fin du chemin. Le premier attribut contient la valeur figurant à la fin du chemin, les suivants contiennent des identifiants d'objets désignant les objets successivement rencontrés en parcourant le chemin à l'envers. La figure XIV.4 illustre un index de chemins simple pour le chemin Produits → Fournisseurs → Pays de la base représentée figure XIV.1.
Une première variante consiste à imbriquer les chemins, en évitant ainsi de répéter plusieurs fois un même identifiant d'objet pour chacun de ses parents. Par exemple, pour le fournisseur F1, on indiquera directement la liste des parents, pour F2 de même, si bien que l'entrée Allemagne de l'index précédent devient (Allemagne(F1(P1, P2) F2 (P1, P3) …). Un tel index est appelé index de chemin imbriqué [Bertino91]. De tels index sont plus difficiles à maintenir et à utiliser que des tables lors des mises à jour.
Les multiindex [Kim89] sont une alternative aux index de chemin. Pour chaque couple de collections (Ci, Ci+1) consécutives du chemin, on gère un index de jointure [Valduriez87] contenant les couples identifiants d'objets liés par le chemin. Le dernier index est un index classique donnant pour chaque valeur terminale du chemin l'identifiant de l'objet contenant cette valeur. Le parcours du chemin s'effectue alors par des intersections de listes d'identifiants. Chaque index est finalement un index classique qui peut être implémenté comme un arbre B. Le problème des multiindex est que chaque index doit être lu ou écrit indépendamment, ce qui nécessite des entrées-sorties supplémentaires par rapport aux index de chemin. L'utilisation de tels index est par contre plus large, par exemple pour accélérer des jointures de collections intermédiaires sur le chemin ou des sélections sur la collection feuille.
XIX-3-3. LIAISON ET INCORPORATION D'OBJETS▲
Dans les SGBD modernes, les objets associés peuvent être stockés ensemble comme un objet composite (c'est-à-dire composés d'autres objets), ou séparément comme plusieurs objets reliés par des identifiants logiques ou physiques. On distingue alors la liaison de l'incorporation d'objets.
Notion XIV.4 : Liaison d'objet (Object linking)
Représentation d'objets associés par un attribut mono (association 1-1) ou multivalué (association 1-N) contenant un ou plusieurs identifiants d'objet pointant depuis un objet vers l'objet associé.
La liaison peut être effectuée dans les deux sens, l'objet référencé pointant lui-même son ou ses objets associés. Il existe alors pour chaque objet cible un ou plusieurs liens inverses vers l'objet source. La liaison est une technique classique pour représenter les associations nécessitant le parcours d'identifiants pour retrouver les objets associés. La liaison inverse permet le parcours de l'association dans les deux sens. La liaison a le mérite de rendre les objets liés quasiment indépendants, ce qui n'est pas le cas avec l'incorporation.
Notion XIV.5 : Incorporation d'objet (Object embedding)
Représentation d'objets associés par un objet composite contenant un objet englobant avec un attribut complexe mono - (association 1-1) ou multivalué (association 1-N) contenant directement la valeur des objets liés.
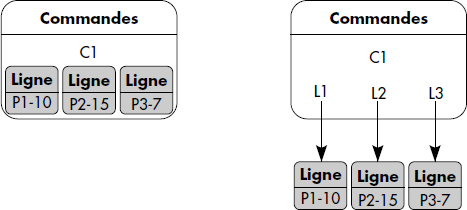
L'incorporation rend les objets incorporés dépendants de l'objet englobant : ils sont détruits avec lui. Le choix entre liaison ou incorporation est donc aussi un problème de sémantique : un objet incorporé a le même cycle de vie que l'objet incorporant. Du point de vue du stockage, l'incorporation présente l'avantage de rendre les objets incorporant et incorporé accessibles simultanément. En outre, elle permet le placement des objets dans une même page, ce qui est aussi possible avec la liaison, comme nous le verrons ci-dessous. Elle présente par contre l'inconvénient de ne pas supporter le partage référentiel des objets dépendants, qui sont de fait copiés s'ils sont référencés ailleurs. La figure XIV.5 illustre la liaison et l'incorporation dans le cas de commandes et de lignes de commandes.
XIX-3-4. GROUPAGE D'OBJETS▲
Pour permettre la navigation rapide d'un objet maître vers des objets liés (par exemple, des commandes aux lignes de commandes) ou pour accélérer les jointures dans le cas d'une implémentation relationnelle, il est possible de grouper différents objets liés dans une même page.
Notion XIV.6 : Groupage (Clustering)
Technique consistant à stocker dans une même page des objets liés par une association afin d'accélérer les accès à ces objets par navigation ou jointure.
Le groupage est plus souple que l'incorporation, car il permet une vie autonome des objets liés, qui peuvent exister sans objets associés. En cas d'objets sans maître ou d'objets partagés par plusieurs maîtres, le choix de la page de stockage n'est pas évident. Pour capturer une large classe de stratégies de groupage, il est possible de définir les groupes par des prédicats de sélection ou d'association. Un prédicat de sélection permet par exemple de définir le groupe des commandes de prix supérieur à 10 000 (Commandes.prix > 10.000). Un prédicat d'association permet par exemple de définir un groupe pour chaque produit (Produits vendu Fournisseurs). Ces prédicats sont utilisés pour définir les ensembles d'objets à stocker ensemble dans une même page ou au moins dans des pages à proximité.
Les prédicats n'étant pas forcément disjoints, un objet peut appartenir logiquement à plusieurs groupes. Si l'on exclut les duplications d'objets, il faut lors du chargement choisir un groupe. Une technique possible consiste à associer des priorités à chaque prédicat de liens. Si un objet appartient à deux groupes ou plus, celui de priorité supérieure est retenu. Pour pouvoir discriminer les groupes, les priorités doivent être différentes, définies par exemple par un nombre de 0 à 10.
Afin de visualiser les informations de spécifications des groupes, il a été proposé [Amsaleg93] d'utiliser un graphe de groupage défini comme suit :
Notion XIV.7 : Graphe de groupage (Clustering graph)
Graphe dont les nœuds représentent les extensions de classes et les arcs les prédicats de liens servant au groupage, chaque arc ayant une priorité pouvant varier de 0 à 10.
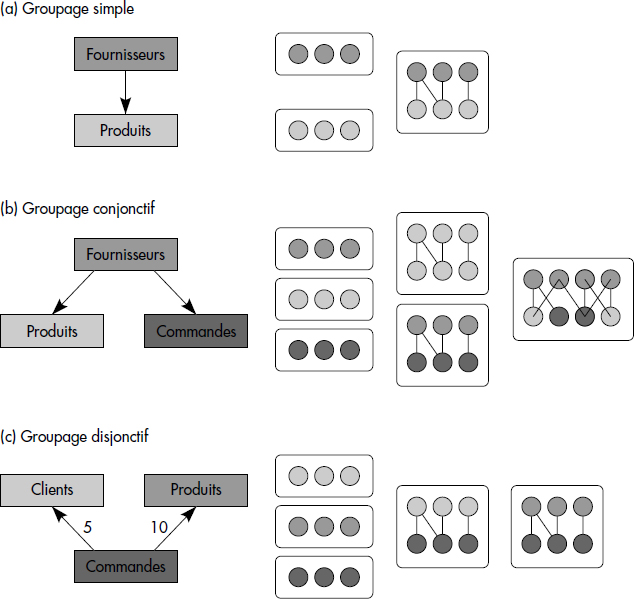
Un graphe de groupage est correct si tous les arcs pointant vers un même nœud ont une priorité différente. Les objets pointés par plusieurs liens de groupage sont donc assignés au groupe de plus forte priorité. La figure XIV.6 présente différents graphes de groupage possibles pour les fournisseurs, les produits et les commandes. Elle suppose que l'association directe des fournisseurs aux produits est gérée par le SGBD. À droite du graphe de groupage, les groupes de différents types possibles sont représentés, par exemple les groupes de fournisseurs, de produits ou les groupes mixtes.
La figure XIV.6 montre quatre possibilités de groupage des objets de collections :
- Le groupage simple. C'est le groupage classique de deux collections selon un prédicat de lien. Ce type de groupage existe dans les bases de données en réseaux (maître et membres via un lien) et est possible dans les bases de données relationnelles selon un prédicat de jointure. Figure XIV.6a, les objets de la collection produits sont groupés simplement avec les objets de la collection fournisseurs, avec une priorité maximale de 10. Tous les produits sans fournisseurs seront groupés ensemble.
- Le groupage conjonctif. Il permet de grouper plusieurs objets de collections différentes avec ceux d'une collection maître. Figure XIV.6b, tous les objets produits et commandes sont groupés avec leurs fournisseurs.
- Le groupage disjonctif. Dans le cas où plusieurs maîtres se partagent un objet qui devrait être groupé avec eux, un choix doit être fait afin d'éviter les duplications d'objets. Selon le mécanisme de priorité, l'objet est alors placé dans le groupe déterminé par l'objet maître selon l'arc de poids maximal. Par exemple, figure XIV.6c, chaque objet commande sera stocké près de son fournisseur s'il existe.
XIX-3-5. SCHÉMA DE STOCKAGE▲
Afin de regrouper et visualiser toutes les informations permettant de stocker les objets dans la base et d'y accéder, nous avons proposé [Gardarin95] d'introduire un graphe de stockage plus complet que le graphe de groupage vu ci-dessus. Ce graphe permet de représenter un schéma objet de données avec des notations proches d'UML (voir chapitre sur la conception), avec en plus les informations suivantes :
- Les objets incorporés liés aux objets incorporants par des flèches doubles en pointillés ;
- Les objets groupés liés aux objets groupants par des flèches simples en pointillés étiquetées par la priorité du groupage et l'éventuel prédicat, s'il ne s'agit de l'association existant entre les objets ;
- Les index par des réseaux de lignes pointillées issus de l'attribut indexé et pointant vers la ou les collections indexées.
La figure XIV.7 représente un exemple de graphe de stockage pour la base dont le schéma a été défini figure XIV.1. Pays est incorporé dans Personnes, dont les attributs sont eux-mêmes incorporés dans Clients et Fournisseurs. Les lignes de commandes sont incorporées dans les commandes. Elles référencent les produits. Les commandes sont placées en priorité à proximité des clients, sinon à proximité des produits. Les produits sont placés à proximité des fournisseurs. Il existe un index de chemin depuis nom de produit vers produits et fournisseurs. Deux index primaires classiques sont gérés, respectivement sur numéro de commande (numco) et numéro de produit (numpro).
Un graphe de stockage induit une organisation physique des données. Il représente en fait le modèle interne de la base et est donc un élément essentiel à prendre en compte pour l'optimiseur. Le problème de l'optimiseur est de trouver le meilleur plan d'accès pour exécuter une requête compte tenu du modèle interne représenté par le graphe de stockage. Pour ce faire, l'optimiseur doit aussi prendre en compte la taille des collections et groupes. Il doit bien sûr optimiser la navigation via des pointeurs, comme nous allons le voir ci-dessous. Notez que la plupart des systèmes objet ne distinguent pas clairement le graphe de stockage et n'ont guère d'optimiseur élaboré capable de bien prendre en compte le modèle interne.
XIX-4. PARCOURS DE CHEMINS▲
Optimiser la navigation dans une base de données objet est l'un des soucis essentiels d'un optimiseur. Ce problème prolonge l'optimisation des séquences de jointures dans les bases de données relationnelles. Dans cette partie, nous présentons plusieurs algorithmes pour évaluer une expression de chemins avec prédicats. De tels algorithmes ont été étudiés dans [Bertino91, Shekita90, Gardarin96]. Ils correspondent à des types variés de traversée d'un graphe d'objets. Un tel graphe est représenté figure XIV.8.
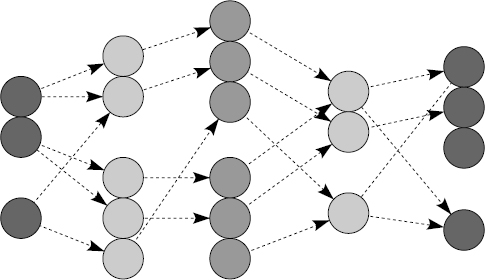
Chaque famille verticale d'objets correspond à une collection Ci (par exemple, une extension de classes). Chaque objet de la collection Ci pointe sur 0 à N objets de la collection Ci+1, selon les cardinalités des associations traversées. Nous écrivons l'expression de chemin C1(P1).C2(P2)…Cn(Pn) en désignant par Pi le prédicat de sélection de la collection Ci. Il s'agit donc d'assembler les séquences c1.c2…cn d'objets liés par des pointeurs et vérifiant respectivement (c1 ∈ C1 et P1), (c2 ∈ C2 et P2)… (cn ∈ Cn et Pn).
XIX-4-1. TRAVERSÉE EN PROFONDEUR D'ABORD▲
La traversée en profondeur d'abord (Depth-First-Fetch, DFF) est la méthode la plus naturelle pour évaluer une expression de chemins avec prédicats. L'algorithme suit le chemin depuis la collection racine vers la collection terminale. Chaque objet est traversé en allant toujours vers le premier objet du niveau supérieur non encore traversé, vers l'objet de même niveau s'il n'en existe pas, et en remontant lorsqu'il n'y a plus d'objet voisin. L'opérateur correspondant est un opérateur n-aire, qui s'applique sur N collections avec un prédicat possiblement vrai (tous les objets qualifient alors) pour chaque collection. DFF peut être vu comme un opérateur de jointures en cascade utilisant une méthode pipeline. La figure XIV.9 donne un sketch de l'algorithme.
// Recherche des objets d'un chemin C1.C2…Cn vérifiant les prédicats P1,P2…Pn
DFF(C1(P1).C2(P2)….Cn(Pn)) {
i = 1 ;
while (i≤n) {
for each x in (Ci) {
if Pi(x) = VRAI {
if i < n return (x + DFF(FETCH(x.Ci+1)(Pi+1)….Cn(Pn)))
else return(x)
}
}
i = i+1 ;
}
}L'avantage de DFF est qu'il s'agit d'un opérateur n-aire qui ne génère pas de résultats intermédiaires. L'algorithme assemble les objets en accédant via les OID, ce qui est efficace dans la plupart des SGBD. Les résultats sont obtenus l'un après l'autre en pipeline. L'algorithme est d'ailleurs très analogue à celui de jointures n-aire en pipeline vu dans le cadre relationnel, à ceci près qu'il navigue en suivant les pointeurs. Ainsi le SGBD peut-il retourner une réponse avant d'avoir traversé tous les objets. Intuitivement, cet opérateur est très efficace lorsque la taille mémoire est suffisante pour contenir tous les objets sur un chemin de la racine aux feuilles, c'est-à-dire au moins une page par collection. Cependant, si les objets ne sont pas groupés selon le chemin et si la taille mémoire est insuffisante, le système peut être conduit à relire de nombreuses fois une même page.
XIX-4-2. TRAVERSÉE EN LARGEUR D'ABORD▲
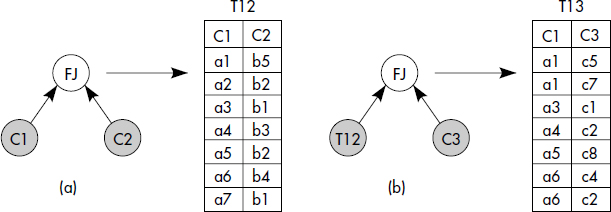
La traversée en largeur d'abord (Breadth-First-Fetch, BFF) parcourt l'arbre d'objets par des jointures binaires en avant (Forward Join, FJ) successives. Les jointures sont effectuées par parcours des pointeurs de la collection Ci vers la collection Ci+1. Ainsi, soit une expression de chemin qualifiée C1(P1).C2(P2)…Cn(Pn). Pour trouver les objets qualifiants, (n-1) jointures par références successives du type Si+1 = FJ(Si→Ci+1(Pi+1)) sont accomplies, où Si désigne une table mémorisant les objets satisfaisant le sous-chemin C1(P1).C2(P2)…Ci(Pi). Le critère de jointure est une simple traversée de pointeurs. Le prédicat Pi+1 doit être vérifié sur les objets cibles de Ci+1. L'algorithme est proche de celui réalisant la traversée en profondeur vue ci-dessus (DFF), mais réduit à deux collections, c'est-à-dire à un chemin de longueur 1. Une table intermédiaire répertoriant les identifiants d'objets qualifiants doit être générée en résultat de chaque jointure en avant. Dans la suite, nous appelons cette table table support. La jointure en avant suivante repart de la table support. La figure XIV.10 illustre l'algorithme de traversée en largeur d'abord pour trois collections, C1, C2 et C3, dont les objets sont notés ai, bi et ci respectivement.
L'avantage de l'algorithme en largeur d'abord est d'être basé sur des jointures binaires par référence, donc précalculées. Le coût de calcul est donc réduit. Cependant, pour accomplir la jointure entre les collections Ci et Ci+1, les états des objets de la première collection Ci doivent être chargés en mémoire pour trouver les pointeurs vers les objets de Ci+1 (contenus dans l'attribut Ai) ; les états de la seconde Ci+1 doivent aussi être chargés en mémoire pour tester le prédicat Pi+1. Si aucun groupage selon l'association n'est réalisé, des accès multiples aléatoires aux pages peuvent être nécessaires. Un tri des identifiants des objets de la deuxième collection sera alors souvent avantageux. Contrairement à l'algorithme DFF, l'algorithme BFF nécessite de conserver si possible en mémoire des résultats intermédiaires. Si l'on veut délivrer tous les objets sur les chemins qualifiants, la table support doit être étendue avec un attribut contenant les identifiants d'objets par collection traversée. L'algorithme ne permet guère de délivrer des résultats avant la traversée totale au moins des n-1 premières collections. Soulignons que dans le cas réduit de deux collections, les algorithmes DFF et BFF sont similaires.
XIX-4-3. TRAVERSÉE À L'ENVERS▲
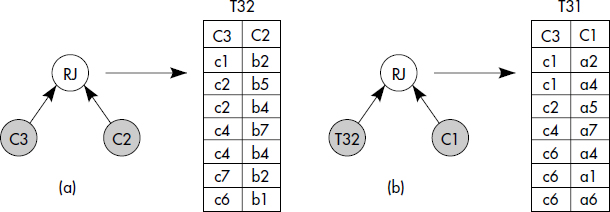
La traversée à l'envers, c'est-à-dire en partant par la dernière collection du chemin, est aussi possible en utilisant un algorithme de jointure binaire classique, de type jointure relationnelle. Comme l'algorithme BFF, la traversée en largeur d'abord à l'envers (Reverse-Breadth-First-Fetch, RBFF) accomplit une séquence de jointures binaires entre collections voisines sur le chemin, mais procède en ordre inverse, donc à reculons. Chaque jointure est appelée une jointure inverse (Reverse Join, RJ). S'il n'y a pas de lien inverse, il s'agit d'une jointure par valeur, c'est-à-dire que le critère est l'appartenance de l'identifiant de l'objet de la seconde collection aux valeurs de l'attribut de liens de la première collection. Pour traiter une expression de chemin qualifiée C1(P1).C2(P2)…Cn(Pn) de la collection C1 à collection Cn, (n-1) jointures successives Si = RJ(Si←Ci(Pi)) sont accomplies, où Si désigne la table support des objets satisfaisant le sous-chemin Ci(Pi)…Cn(Pn) ; RJ est l'algorithme de jointure inverse testant l'appartenance de l'identifiant aux pointeurs. Une technique de jointure par hachage ou par tri-fusion peut être appliquée. La traversée à l'envers est illustrée figure XIV.11.
La traversée à l'envers est avantageuse lorsqu'une sélection directe est possible sur la dernière collection (par exemple par un index) et que cette sélection retrouve un nombre faible d'objets (forte sélectivité). Pour mémoriser le parcours, une table support est générée (voir figure XIV.11). Un avantage de la méthode est qu'à chaque pas la jointure est faite entre cette table support et la collection précédente sur le chemin. L'algorithme est bon si la table support est petite (expression de chemin sélective).
Soulignons qu'une expression de chemins peut toujours être divisée en plusieurs sous-expressions, chacune pouvant être traitée avec un algorithme différent, DFF, BFF ou RBFF. Si un prédicat très sélectif est rapidement évaluable sur une collection du chemin, on aura avantage à considérer RBFF pour la partie préfixant cette collection, puis BFF ou DFF pour la partie suffixe. Le choix d'un algorithme ou d'un autre n'est pas évident et nécessite un modèle de coût, comme nous le verrons plus loin.
XIX-4-4. TRAVERSÉE PAR INDEX DE CHEMIN▲
La traversée par index de chemin (Path Index Traversal, PIT) bénéficie de l'existence d'un index suivant le chemin. Comme vu ci-dessus, pour une valeur d'attribut de la collection cible, l'index donne tous les sous-chemins qualifiants. Il suffit donc d'accéder à l'index pour trouver les associations d'objets satisfaisant le prédicat. Cependant, si d'autres prédicats figurent dans les collections précédant la collection indexée, il faut accéder aux objets associés dont les identifiants sont trouvés dans l'index. Cela peut être très pénalisant si les accès sont éparpillés sur les disques. Des tris sur les identifiants physiques d'objets seront souvent avantageux, car ils permettront de grouper les accès aux objets d'une même page. Une autre faiblesse des index de chemins est bien sûr les coûts de maintenance lors des mises à jour, souvent importants.
XIX-5. GÉNÉRATION DES PLANS ÉQUIVALENTS▲
XIX-5-1. NOTION D'OPTIMISEUR EXTENSIBLE▲
Plus qu'en relationnel, la génération de plans équivalents doit se faire par application de règles de transformation. En effet, à la différence des systèmes relationnels, les systèmes objet ou objet-relationnels ne sont pas fermés : l'implémenteur de bases de données peut ajouter ses propres types de données obéissant à des règles spécifiques de transformation, comme les types géométriques (point, cercle, etc.) vus ci-dessus. Un optimiseur d'un SGBD objet ou objet-relationnel doit donc être extensible.
Notion XIV.8 : Optimiseur extensible (Extensible optimiser)
Optimiseur capable d'enregistrer de nouveaux opérateurs, de nouvelles règles de transformation de plans, de nouvelles fonctions de coût et de nouvelles méthodes d'accès lors de la définition de types de données utilisateurs, ceci afin de les utiliser pour optimiser les requêtes utilisant ces types.
Cette notion d'optimiseur extensible a été bien formalisée pour la première fois dans [Grafe93]. Un optimiseur extensible est construit autour d'une base de connaissance mémorisant les définitions de types et opérateurs associés, de méthodes d'accès, de fonctions de coût et de règles de transformation de plans d'exécution. Toutes les transformations de plans peuvent être exprimées sous la forme de règles. Comme en relationnel, les règles permettent de transformer les arbres d'opérateurs de l'algèbre représentant les requêtes en arbres équivalents. Au-delà du relationnel, pour supporter les types de données utilisateurs, l'algèbre relationnelle doit être étendue en une algèbre d'objets complexes, avec en particulier les fonctions dans les expressions de qualification et de projection, et le support d'opérations sur collections imbriquées telles que Nest, Unnest et Flatten. Une telle algèbre a été présentée au chapitre XI.
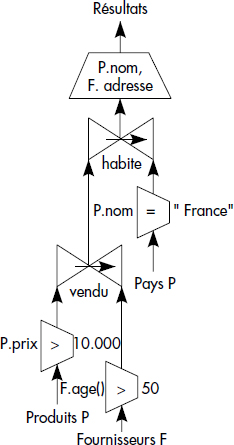
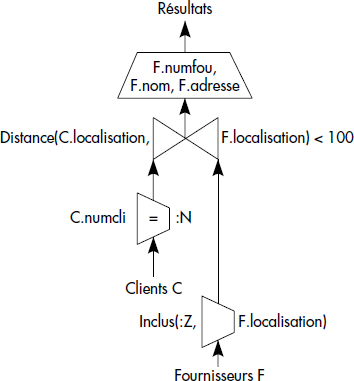
Nous représentons figures XIV.12 et XIV.13 les questions Q1 et Q3 du paragraphe 2.2 sous la forme d'arbres algébriques. L'arbre de la figure XIV.12 contient trois restrictions sur attributs ou méthodes, suivies de deux jointures par références qui traduisent le parcours de chemin. Ces deux jointures peuvent par exemple être remplacées par un opérateur de parcours du graphe en profondeur d'abord (DFF) vu ci-dessus, ou par des jointures en arrière (RBFF). Une projection finale gagnerait à être descendue par les règles classiques vues en relationnel.
L'arbre de la figure XIV.13 présente une restriction sur prédicats utilisateurs (Inclus) et une jointure sur fonction utilisateur (Distance < 100). L'optimisation de telles requêtes est difficile et nécessite des connaissances spécifiques sur les fonctions utilisateur [Hellerstein93], ici des fonctions géométriques.
XIX-5-2. LES TYPES DE RÈGLES DE TRANSFORMATION DE PLANS▲
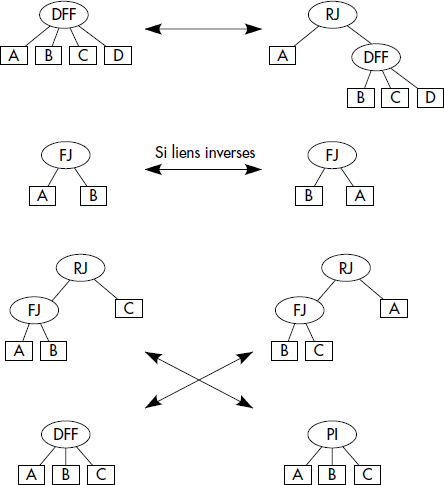
Comme pour le relationnel, un plan d'exécution est un arbre annoté, l'annotation associée à chaque opérateur spécifiant l'algorithme choisi. Une règle exprime que lorsqu'un sous-arbre annoté est rencontré dans un plan d'exécution, il peut être remplacé par un autre sous-arbre annoté sous certaines conditions. Le choix d'un langage de règles pour écrire les règles de transformation est un problème difficile [Finance94]. Certaines sont simplement des règles d'équivalence, conduisant à des transformations applicables dans les deux sens. Nous les noterons simplement :
<SOUS-ARBRE> ⇔ <SOUS-ARBRE>D'autres règles ne sont applicables que dans un sens et peuvent nécessiter des conditions. À titre d'exemple, nous les écrirons sous la forme suivante :
<SOUS-ARBRE> [<CONDITION>] ⇒ <SOUS-ARBRE>Une telle règle signifie que lorsqu'un sous arbre est rencontré, si la condition optionnelle est satisfaite, il peut être réécrit dans le sous-arbre figurant après l'implication. En pratique, il faut en plus appliquer quelques procédures, par exemple pour changer des variables ou des annotations ; celles-ci sont supposées attachées à la règle ; elles ne sont pas mentionnées pour des raisons de simplicité.
XIX-5-2-1. Règles syntaxiques▲
Les premières règles que l'on peut exprimer simplement sont celles caractérisant les propriétés de l'algèbre, déjà vues dans le cadre relationnel pour la plupart. Par exemple, la règle d'associativité des jointures s'écrira simplement
JOIN(JOIN(X,Y),Z) ⇔ JOIN(X,JOIN(Y,Z));Plus complexe, la règle de permutation de la projection sur un schéma Z de la jointure naturelle de deux relations de schémas X et Y nécessite une condition :
PROJECT(JOIN(X,Y), Z) [X∩Y ∈ Z] ⇒
JOIN(PROJECT(X,Z∩X),PROJECT(Y,Z∩Y);Toutes les règles classiques de l'algèbre relationnelle peuvent ainsi être codées, avec plus ou moins de difficultés. Il est possible aussi d'ajouter des règles prenant en compte les opérations sur collections, NEST, UNNEST et FLATTEN. Par exemple, la règle permettant de pousser une restriction avant une opération d'imbrication NEST peut s'écrire :
RESTRICT(NEST(X, G, N), Q) [ ∃ ATTRIBUT(Q) ∈ G ] ⇒
RESTRICT(NEST(RESTRICT(X, Q1), G, N), Q2);Cette règle exprime le fait que si une restriction est appliquée sur certains attributs de groupement, alors la partie de la restriction concernant ces attributs peut être appliquée avant le groupement.
Au-delà, des règles de simplification peuvent aussi être introduites pour isoler des sous-arbres identiques et les remplacer par une relation intermédiaire utilisable en plusieurs points. Ce genre de règles est important, car il permet d'éviter de calculer deux fois la même sous-question. Son expression générale nécessite un langage de règles un peu plus puissant, permettant de tester si deux sous-arbres sont équivalents.
XIX-5-2-2. Règles sémantiques▲
Nous groupons dans cette catégorie toutes les règles générales permettant de générer des questions équivalentes soit en prenant en compte des règles d'intégrité des données, soit en exprimant des axiomes sur les types de données abstraits.
XIX-5-2-2-1. Contraintes d'intégrité▲
La prise en compte des contraintes sur les données dans les bases de données objet ou objet-relationnelles est difficile. Un optimiseur capable de prendre en compte de telles contraintes pour un SGBD objet a été développé à l'INRIA [Florescu96]. Une contrainte est exprimée sous la forme suivante :
[FOR ALL [<VARIABLE> OF TYPE <TYPE>]*] <EXPRESSION> ⇔ <EXPRESSION>Les expressions sont des termes fonctionnels du langage OQL, c'est-à-dire des expressions de chemins, des prédicats avec expressions de chemins ou des requêtes. De telles règles permettent d'exprimer divers types de contraintes, comme l'existence de liens inverses et la redondance de données. Considérons par exemple la définition en ODL de la base décrivant pays et clients, en supposant ces classes liées par une association 1→N :
INTERFACE CLIENTS {
ATTRIBUT INT NUMCLI KEY, STRING NOM,
ADRESSE CADRESSE, REF(PAYS) CPAYS, INT TELEPHONE,
INT SEGMENT, STRING COMMENTAIRE
}
INTERFACE PAYS {
ATTRIBUT INT NUMPAYS KEY, STRING NOM, INT NUMCONT,
STRING COMMENTAIRE, RESIDENTS SET <CLIENTS>
}La règle de lien inverse spécifiant qu'un client référence un pays s'il est résident de ce pays s'écrit :
FOR ALL C OF TYPE CLIENTS, P OF TYPE PAYS
C.CPAYS = P ⇔ C IN P.RESIDENTSSupposons en plus que les adresses contiennent le pays :
INTERFACE ADRESSE {
ATTRIBUT INT NUM, STRING RUE,
STRING VILLE, INT ZIP, STRING PAYS
}Une règle exprimant une redondance de valeurs est :
FOR ALL C OF TYPE CLIENTS
C.CADRESSE.PAYS ⇔ C.CPAYS.NOMDe telles équivalences sont très puissantes et permettent d'exprimer toutes sortes de redondances, par exemple l'existence de vues matérialisées ; l'équivalence peut être remplacée par une implication. Les équivalences ou implications peuvent être facilement étendues pour exprimer des impossibilités, telles que la valeur nulle interdite ou l'unicité de clé (absence de doubles). Il est aussi possible de prendre en compte des assertions d'inclusion et des assertions d'appartenance [Florescu96].
Par exemple, une règle exprimant la non-nullité de l'attribut pays peut s'écrire :
FOR ALL C OF TYPE CLIENTS C
C.CPAYS = NIL ⇔Une règle exprimant l'unicité de la clé de client s'écrit :
FOR ALL C1,C2 OF TYPE CLIENTS
C1.NUMCLI = C2.NUMCLI ⇔ C1 = C2XIX-5-2-2-2. Types abstraits de données▲
L'équivalence de termes constitue un langage de règles puissant qui peut aussi être adapté aux types abstraits de données. Ajoutons à la base précédente des images décrivant nos clients définies comme suit :
INTERFACE IMAGE {
ATTRIBUT NUMCLI INT, CONTENT ARRAY[1024,1024] INT,
OPERATION
ARRAY[10] SUMMARY(IMAGE),
IMAGE ROTATE (IMAGE, ANGLE),
IMAGE CLIP (REGION)
}Considérons la requête suivante qui recherche les images des clients du segment 5, les intersecte avec une fenêtre prédéfinie $zone, et les fait tourner de 90° avant de les afficher :
SELECT CLIP(ROTATE(I,90),$ZONE)
FROM CLIENTS C, IMAGES I
WHERE C.NUMCLI = I.NUMCLI
AND C.SEGMENT = 5 ;Il apparaît que, plutôt que de faire tourner les images, on aurait intérêt à faire l'intersection (le clip) avec la zone tournée de - 90°, et à faire tourner seulement la partie intéressante. L'équivalence de termes est aussi très appropriée à la définition d'axiomes sur des types abstraits. Par exemple, la transformation nécessaire pour réécrire la question précédente de manière plus optimisée est :
FOR ALL I OF IMAGE, F OF FENETRE
CLIP(ROTATE(I,$A), F) ⇔ ROTATE(CLIP(I,ROTATE(F,-$A),$A)On découvre alors la question équivalente en principe plus rapide à exécuter :
SELECT ROTATE (CLIP(I, ROTATE($ZONE,-90)),90)
FROM CLIENTS C, IMAGES I
WHERE C.NUMCLI = I.NUMCLI
AND C.SEGMENT = 5;Plus généralement, de telles règles permettent de prendre en compte les spécificités des types abstraits afin de réécrire les expressions de fonctions dans les requêtes. Elles permettraient par exemple de spécifier des connaissances géométriques suffisantes pour montrer que les questions Q3 et Q4 vues dans la section sur les motivations sont équivalentes.
XIX-5-2-3. Règles de planning▲
Pour générer l'espace de recherche des plans, il faut bien sûr ajouter les règles permettant de choisir les algorithmes de sélection, jointures, et plus généralement les traversées de chemins qualifiés. Pour les systèmes relationnels, les règles de planning sont bien connues [Ioannidis90, Ioannidis91]. Pour les jointures, elles permettent par exemple de choisir le meilleur algorithme parmi le tri-fusion (SORT-MERGE), les boucles imbriquées (NESTED-LOOP) et la construction d'une table de hachage (HASH-TABLE). Ces règles peuvent s'exprimer comme suit :
JOIN SORT-MERGE (X,Y) ⇔ JOIN NESTED-LOOP (X,Y)
JOIN SORT-MERGE (X,Y) ⇔ JOIN HASH-TABLE(X,Y)Pour les systèmes objet, il est possible de les étendre [Gardarin96] par quelques règles permettant de prendre en compte les traversées de chemin, avec les algorithmes présentés dans la section 4. Ces nouvelles règles concernent l'utilisation de l'opérateur DFF de parcours en profondeur d'abord, des jointures par références et des index de chemins. JOINFJ désigne la jointure par référence en avant non considérée ci-dessus et JOINRJ la jointure par référence en arrière. JOINPATH-INDEX désigne l'algorithme de jointure exploitant l'existence d'un index de chemin. On obtient les nouvelles règles :
-
Jointure en avant ou en arrière :
SélectionnezA JOINFJ B ⇔ A JOINRJ B -
Découpage et groupage de traversées en profondeur d'abord :
SélectionnezDFF(A,B,C…N)⇔JOIN(DFF(A,B..x-1),DFF(x…N)) - Utilisation d'index de chemin :
JOINFJ(X,Y) [PATH-INDEX(X,Y)] ⇒ JOINPATH-INDEX(X,Y)
DFF(A,B,C…N)[PATH-INDEX(A,B,C…N)] ⇒ JOINPATH-INDEX(X,Y)XIX-5-3. TAILLE DE L'ESPACE DE RECHERCHE▲
Quelle est la taille de l'espace de recherche des plans pour une question donnée ? Tout dépend bien sûr de la forme de la question et des règles qui s'y appliquent. En général, l'optimisation de requêtes objet conduit à des espaces de recherche plus grands que pour les requêtes relationnelles. Cela provient surtout du fait que les requêtes sont souvent plus complexes et les règles de transformation plus nombreuses.
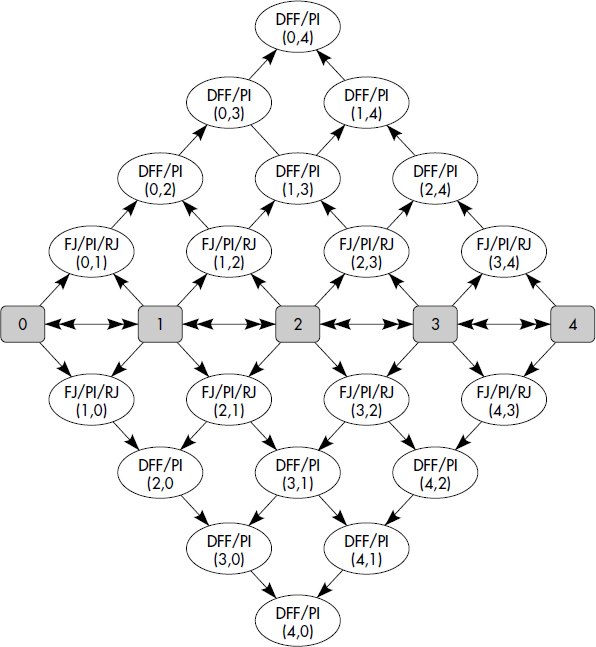
Prenons par exemple le cas d'une expression de chemin linéaire qualifiée. De telles requêtes s'appellent des requêtes chaînes (voir figure XIV.14). Le profil de requêtes OQL correspondant est :
SELECT (X1, X2….Xn)
FROM X1 IN C1, X2 IN C1.AC2….Xn IN Cn-1.ACn
WHERE …Pour simplifier, supposons l'absence d'index de chemins. Chaque collection est reliée à chacune de ses voisines par une association multivaluée (le cas monovalué est un cas dégénéré).
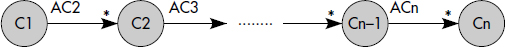
FJ et RJ sont les deux algorithmes de jointures, l'un par parcours de référence en avant (FJ), l'autre par jointure sur valeur de référence en arrière (RJ). DFF est l'opérateur n-aire de jointure par référence parcourant le graphe en profondeur d'abord. Dans le cas où DFF n'est pas utilisé, le problème revient à calculer le nombre d'ordres de jointures possibles avec deux opérateurs de jointures en évitant les produits cartésiens [Tan91], [Lanzelotte93]. On obtient pour l'espace de recherche de jointures binaires de n collections :
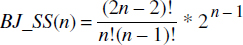
Si l'on introduit l'opérateur DFF, la taille de l'espace de recherche devient bien sûr plus grande. Soit SS(n-1) l'espace de recherche pour traverser (n-1) collections. On a :
SS(n) = BJ_SS(n) + PC_SS(n)BJ_SS(n) est l'espace de recherche pour les jointures binaires et PC_SS(n) est le nombre d'arbres annotés avec au moins un nœud DFF. Pour déterminer la valeur de PC_SS(n), supposons tout d'abord un seul DFF avec trois collections : celles-ci sont traitées ensemble par cet opérateur DFF et peuvent être vues comme une unique collection ; pour le reste, la longueur du chemin est réduite de 2, ce qui signifie que SS(n - 2) plans peuvent être générés. Il existe n - 2 positions parmi les n collections où il est possible d'appliquer l'opérateur DFF sur trois collections. Pour la même raison, il existe n - 3 positions où appliquer DFF sur quatre collections ; et ainsi de suite ; finalement, il existe 2 positions où appliquer DFF sur n - 1 collections et 1 position pour appliquer DFF sur les n collections. En sommant tous les cas analysés, on obtient une borne supérieure de PC_SS(n). Ainsi, une bonne approximation du nombre de plans est :
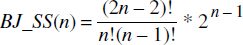
avec SS(1) = 1, SS(2) = 2, SS(3) = 9.
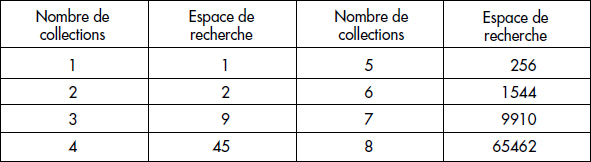
Ainsi, la table présentée figure XIV.15 donne une approximation du nombre de plans pour des chemins de longueur 1 à 8. On constate qu'au-delà de 8, l'espace devient rapidement important. Il est donc très coûteux pour un optimiseur de considérer toutes les solutions, surtout dans les cas de requêtes plus complexes que les requêtes chaînes.
XIX-5-4. ARCHITECTURE D'UN OPTIMISEUR EXTENSIBLE▲
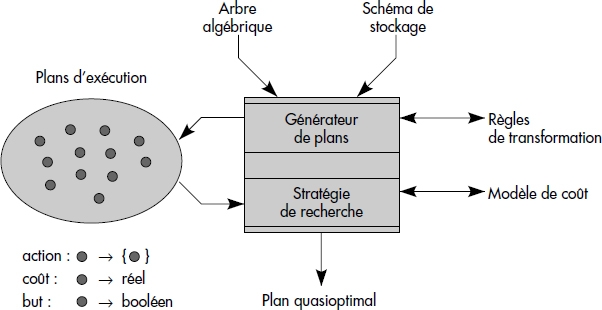
Un optimiseur extensible doit donc permettre la prise en compte complète de nouveaux types de données, avec opérateurs, règles, etc. Il s'agit donc d'un véritable système expert spécialisé. La figure XIV.16 représente une architecture possible pour un optimiseur extensible [Lanzelotte91]. Celui-ci explore l'espace des plans d'exécution. Un tel optimiseur accepte de l'administrateur la définition de règles de transformation d'arbres algébriques annotés. Il est extensible, en ce sens qu'il est possible d'ajouter de nouveaux types et de nouvelles règles. Il transforme un arbre algébrique d'entrée en un plan d'exécution quasiment optimal. Pour cela, il utilise le schéma de stockage de la base. Le générateur de plan applique les règles. La stratégie d'évaluation est basée sur un modèle de coût et tend à réduire le nombre de plans explorés afin d'atteindre le but qui est un plan de coût proche du minimal possible, dit quasi optimal.
XIX-6. MODÈLE DE COÛT POUR BD OBJET▲
Un modèle de coût est un ensemble de formules permettant d'estimer le coût d'un plan d'exécution. Un optimiseur basé sur un modèle de coût cherche à sélectionner le plan de coût minimal parmi les plans équivalents. Le coût d'un plan se compose de plusieurs composants : le coût de calcul (CPU_Cost), le coût d'entrée-sorties (IO_Cost), éventuellement le coût de communication (COM_Cost). Le premier correspond au temps passé à exécuter des instructions de l'unité centrale, par exemple pour évaluer un prédicat ou exécuter une boucle. Le deuxième correspond au temps de lecture et écriture sur disques. Le troisième intervient surtout dans les bases réparties où des échanges de messages sont nécessaires sur le réseau.
Dans cette section, nous présentons un modèle de coût pour bases de données objet, publié dans [Gardarin95]. Considérant une base centralisée, nous évaluons seulement les coûts d'entrées-sorties et de calcul. Pour simplifier, nous supposons que les objets ont une taille inférieure à une page et que les valeurs d'attributs sont uniformément distribuées à l'intérieur de leurs domaines de variation.
XIX-6-1. PRINCIPAUX PARAMÈTRES D'UN MODÈLE DE COÛT▲
Le modèle de coût utilise des statistiques sur les données de la base pour estimer le coût d'une opération. Ces statistiques se composent d'informations sur les collections de la base comme la cardinalité (nombre d'objets) de ces collections, la taille moyenne des objets, le nombre de valeurs distinctes d'un attribut, la présence d'index et de groupes d'objets. Un bon modèle de coût doit prendre en compte le placement des objets dans des groupes (clustering). En effet, une collection C peut être divisée en n groupes notés C1, C2…Cn. Les techniques de groupage permettent de placer dans un même groupe des objets de collections différentes.
Plus précisément, pour chaque collection d'objets C nous utilisons les statistiques suivantes :
- ||C|| la cardinalité de la collection C,
- |C| le nombre de pages de la collection C,
- ||Ci|| la cardinalité du groupe i de la collection C,
- |Ci| le nombre de pages du groupe i de la collection C,
- SC la taille moyenne des objets dans la collection C.
Afin d'évaluer le coût de la navigation entre objets, il est nécessaire d'estimer finement les cardinalités des associations entre collections. Soient deux collections C1 et C2 reliées par un chemin de traversée implémenté par des pointeurs de C1 vers C2. Un tel chemin C1 → C2 sera caractérisé par les statistiques suivantes :
- FanC1,C2 le nombre moyen de références d'un objet de C1 vers des objets de C2 ;
- DC1,C2 le nombre moyen de références distinctes d'un objet de C1 vers des objets de C2 ;
- XC1,C2 le nombre d'objets de C1 n'ayant pas de références (ou des références nulles) vers des objets de C2.
À partir de ces paramètres, nous pouvons calculer le nombre de références distinctes des objets de C1 ayant au moins une référence non nulle vers des objets de C2 par la formule :
De plus, nous supposons connus les paramètres suivants, dépendant essentiellement de choix d'implémentation du système :
- b le degré moyen des arbres-B utilisés (par exemple 256 clés par page) ;
- BLevel(I) le nombre de niveaux d'un index I (souvent 3) ;
- Sp la taille d'une page (par exemple 4K) ;
- Proj_Cost le coût moyen d'extraction d'un attribut d'un objet ;
- m la taille mémoire disponible en page ;
- Cost_load_page le coût de chargement d'une page en mémoire (une E/S).
Tous ces paramètres sont donc utilisés par le modèle de coût détaillé ci-dessous.
XIX-6-2. ESTIMATION DU NOMBRE DE PAGES D'UNE COLLECTION GROUPÉE▲
Lorsque plusieurs collections sont groupées ensemble par des associations, il n'est pas évident de déterminer le nombre de pages à balayer pour trouver les objets dans l'une d'elles. Si une collection A n'est pas groupée avec d'autres collections, il y a ![]() objets au plus dans une page et le nombre total de pages après chargement séquentiel peut être calculé comme suit :
objets au plus dans une page et le nombre total de pages après chargement séquentiel peut être calculé comme suit :
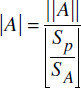
Dans le cas de plusieurs collections groupées, certaines pages peuvent être homogènes, d'autres contenir des objets de différentes collections. Une méthode pour estimer le nombre total de pages d'une collection groupée avec d'autres a été proposée dans [Tang96]. Supposons que la collection B soit groupée avec la collection A (voir figure XIV.17). Rappelons que nous notons respectivement SA et SB les tailles moyennes des objets des collections A et B, et que SA et SB sont supposées inférieures à la taille de la page. Estimons tout d'abord la taille de la collection A qui est la racine de l'arbre de groupage. Il existe deux partitions physiques pour A après le placement des deux collections, l'une contenant des objets groupés avec des objets de B notée ClA→B, l'autre ne contenant que des objets de A notée ClA.
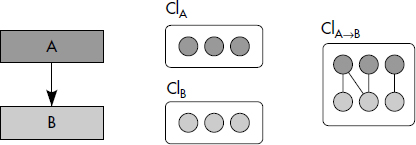
La partition ClA contient les objets A ne référençant pas d'objets B, donc ||ClA||=XA,B, d'où l'on déduit la taille de cette partition :
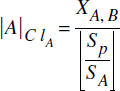
Pour ClA→B, le nombre d'objets de A dans cette partition est ||A||-XA,B. La taille d'un groupe autour d'un objet A est SClA→B = SA+(ZA,B*SB), d'où l'on déduit :
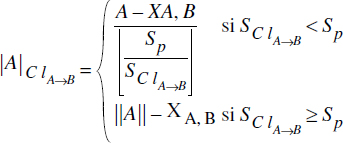
Le nombre total de pages de la collection A est donc donné par :
|A| = |A|ClA + |A|ClA→BD'une manière similaire, nous pouvons estimer le nombre de pages de la collection B, une collection non-racine dans le graphe de placement. Les différentes partitions composant la collection B sont notées ClA→B et ClB.
-
Pour ClB, le nombre d'objets de B non référencés par un quelconque objet de A est ||B||-(||A||*DA,B), d'où nous déduisons :
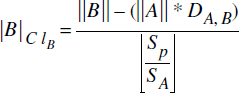
- Pour ClA→B, la taille et le nombre d'objets par groupe reste le même que celui calculé ci-dessus, mais le nombre de groupes auxquels accéder est maintenant X'ClA→B= Min(ZA,B*XA,B, XA,B). Nous obtenons donc :
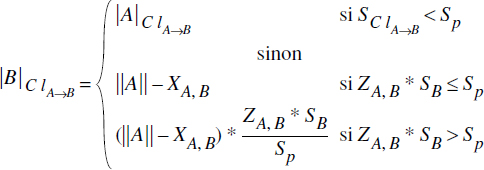
Le nombre total de pages de la collection B est obtenu par :
|B| = |B|ClA + |B|ClA→BAinsi, en étudiant la taille des différentes partitions, il est possible de calculer la taille globale en nombre de pages d'une collection groupée.
XIX-6-3. FORMULE DE YAO ET EXTENSION AUX COLLECTIONS GROUPÉES▲
Le modèle de coût doit permettre de calculer le nombre de pages auxquelles accéder lors d'une sélection d'une collection par un prédicat. Dans le cas de bases de données relationnelles, la formule de Yao [Yao77] permet de calculer le nombre de blocs contenant au moins un enregistrement lors d'une sélection de k enregistrements parmi n.
Notion XIV.9 : Formule de Yao (Yao Formula)
Formule permettant de calculer le nombre de blocs auxquels accéder lors d'une sélection de k enregistrements parmi n (k≤n) uniformément distribués dans m blocs (1<m≤n) comme suit :
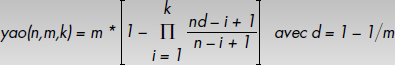
Dans le cas d'une collection C groupée avec d'autres, il n'est pas possible d'appliquer simplement la formule de Yao pour estimer le nombre de pages auxquelles accéder lors d'une sélection par un prédicat P par Yao(||C||,|C|,Sel(P)*||C||). Le problème est qu'une collection groupée est composée de plusieurs partitions. Certains objets sont groupés avec des objets de collections différentes. Ainsi, la distribution des objets dans les pages n'est pas uniforme, bien que les collections soient supposées indépendantes d'un point de vue probabiliste. Il est possible d'appliquer la formule de Yao à chaque partition, après avoir déterminé la taille de chaque partition comme vu ci-dessus, soit ||C||i objets et |C|i pages pour la partition i. Nous obtenons alors la formule de Tang pour le calcul des entrées-sorties [Tang96].
Notion XIV.10 : Formule de Tang (Tang Formula)
Étant donné une collection C divisée en p partitions, chacune ayant ||C||i objets et ||C||i pages, la sélection aléatoire de k objets de C nécessite l'accès à :
![]()
où ki est le nombre d'objets sélectionnés dans la partition Ci.
Si les objets à sélectionner sont placés uniformément dans les partitions, on sélectionne ki = (||Ci||/||C||)*k dans la partition i. Quand les objets qui satisfont le prédicat de recherche ne sont pas placés uniformément, il faut calculer la sélectivité du prédicat dans chaque partition pour calculer ki. Bien que dérivée de la formule de Yao, la formule de Tang est plus générale que celle de Yao, qui en est un cas particulier pour une collection avec une seule partition.
XIX-6-4. COÛT D'INVOCATION DE MÉTHODES▲
Avec l'approche objet, les attributs peuvent être publics ou privés. Les attributs publics sont directement accessibles et le coût d'extraction peut être assimilé à une constante. Il peut aussi être plus précisément déterminé en fonction du type de l'attribut et de sa longueur en octets.
Les attributs privés sont manipulés par des méthodes. Déterminer le coût d'une méthode n'est pas chose simple. Deux approches ont été proposées pour cela.
Notion XIV.11 : Révélation de coût (Cost révélation)
Technique consistant à fournir une méthode de calcul de coût associée à chaque opération d'une classe, avec des paramètres identiques ou simplifiés.
Par exemple, si une classe Géométrie publie une fonction distance(géométrie), elle pourra aussi publier une fonction coût_distance(géométrie). Le coût pourra être très différent selon les géométries sur lesquelles s'applique la fonction : il est par exemple beaucoup plus simple de calculer la distance de deux points que celle de deux polygones.
Notion XIV.12 : Moyennage de coût (Cost averaging)
Technique consistant à mémoriser le coût moyen d'application d'une méthode au fur et à mesure de son utilisation.
Au départ, le coût de la méthode est inconnu, et estimé par exemple comme une projection sur attribut. Puis, suite aux requêtes ou à des demandes d'estimation de l'administrateur (par une requête spécifique ANALYZE <méthode>), la méthode est exécutée sur un échantillon de N objets. Une table est gérée dans la métabase pour maintenir le coût moyen observé, de schéma simplifié COSTMETHOD (coût real, nombre int), coût étant le coût moyen et nombre le nombre d'exécutions observées. La table peut aussi mémoriser le type des paramètres, les heures d'appels, etc., afin d'obtenir des statistiques plus fines.
XIX-6-5. COÛT DE NAVIGATION VIA EXPRESSION DE CHEMIN▲
Ce coût dépend évidemment de l'algorithme de traversée de chemin utilisé. Nous analysons ici le cas où une expression de chemin avec prédicats est évaluée en utilisant l'algorithme en profondeur d'abord (DFF) vu ci-dessus. Soit une expression de chemin entre des collections C1, C2…Cn qualifiée par des prédicats P1, P2…Pn à chaque niveau. Une telle expression est notée C1 (P1).C2 (P2)… Cn(Pn). Désignons par Ai l'attribut de Ci-1 référençant un ou plusieurs objets de la collection Ci. Soit Si la sélectivité du prédicat Pi (Si = Sel(Pi)). L'algorithme DFF accède successivement, pour chaque objet de la collection de niveau i satisfaisant le prédicat Pi, à l'attribut pointant sur les objets de la collection (i+1). Suivant ces liens, il lit les pages successives des collections en profondeur d'abord. Pour simplifier, nous supposons qu'il existe au moins une page disponible en mémoire par collection.
Calculons tout d'abord le nombre de références Refi distinctes moyennes pointant d'un objet de la collection Ci-1 vers un objet de Ci dans le chemin, soit Refi = (1-Probi)*||Ci||. Probi est la probabilité qu'un objet de la collection Ci ne soit pas pris en compte dans le chemin, probabilité calculée par la formule :
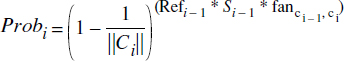
Selon la taille mémoire disponible, trois cas sont possibles :
- Si la mémoire disponible p est assez grande pour contenir toutes les pages du chemin, chaque page est chargée une fois et une seule. Selon que le groupage est effectué par la référence ou non, on effectue l'accès à Refi objet de la collection en 0 ou en Tang(Ci,Refi) entrées-sorties, d'où l'on calcule le nombre de pages lues :
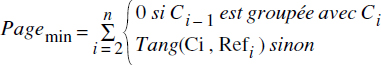
- Si le nombre de pages disponibles en mémoire p est exactement la taille du chemin (p = n), nous obtenons le cas limite très défavorable :
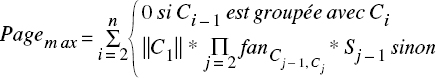
- Si le nombre de pages disponibles en mémoire p est compris entre n et Pagemin, la mémoire ne peut contenir toutes les pages nécessaires à l'évaluation de l'expression de chemin. Le coût d'entrées-sorties dépend de la politique de remplacement des pages du SGBD. Certaines pages devront être lues plusieurs fois. Il est possible d'approcher le nombre d'entrées-sorties par une fonction linéaire entre Pagemin et Pagemax, comme suit :
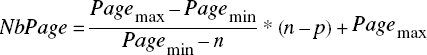
Finalement, le coût d'évaluation d'un prédicat P constitué d'une expression de chemin qualifiée avec p pages disponibles en mémoire centrale est :
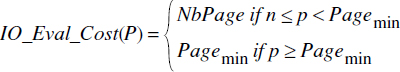
Le coût de calcul associé à l'évaluation d'un tel prédicat est le coût de projection plus le coût d'évaluation des prédicats élémentaires pour chaque objet traversé, soit :
CPU_Eval_Cost(P) = ||C1|| * (CPU_Pr oj_Cost)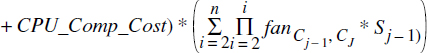
XIX-6-6. COÛT DE JOINTURE▲
En dehors des parcours de références évalués ci-dessus pour l'algorithme DFF, les algorithmes de jointures sont analogues à ceux des bases relationnelles. Vous pouvez donc vous reporter au chapitre concernant l'optimisation de requêtes dans les BD relationnelles pour trouver les formules de coût applicables. Des formules plus détaillées pourront être trouvées dans [Harris96]. Plus généralement, en dehors du groupage des objets, des parcours de références et des index de chemins, les BD objet n'ont guère d'autres spécificités d'implémentation.
XIX-7. STRATÉGIES DE RECHERCHE DU MEILLEUR PLAN▲
La recherche du meilleur plan d'exécution dans une base de données objet ou objet-relationnelle est encore plus complexe que dans une base relationnelle. En effet, l'espace des plans est plus large du fait de la présence de références, d'index de chemins, de collections imbriquées, etc. Au-delà de la programmation dynamique classique limitée à des espaces de recherche de faible taille [Swami88, Swami89, Vance96] vue dans le cadre relationnel, des méthodes d'optimisation pour la recherche de plans optimaux basées sur des algorithmes aléatoires ont été proposées. Après les avoir présentés, nous proposons une méthode plus avancée basée sur des algorithmes génétiques.
XIX-7-1. LES ALGORITHMES COMBINATOIRES▲
Les algorithmes combinatoires accomplissent une marche au hasard dans l'espace de recherche sous la forme d'une suite de déplacements. Un déplacement dans cet espace est généré par application d'une règle de transformation sur le plan d'exécution. Un déplacement est appelé descendant s'il diminue le coût du plan, montant s'il l'augmente. Un état (donc un plan) est un minimum local si tout déplacement unitaire augmente son coût. Le minimum global est celui parmi les minima locaux qui a le plus faible coût. Cette classe d'algorithmes inclut l'amélioration itérative (Iterative Improvement [Nahar86]), le recuit simulé (Simulated Annealing [Ioannidis87]), l'optimisation deux phases (Two Phase Optimization [Ioannidis90]) et la recherche taboue (Tabu Search [Glover89, Glover90]). Nous présentons en détail ces méthodes ci-dessous.
XIX-7-2. L'AMÉLIORATION ITÉRATIVE (II)▲
L'amélioration itérative commence par un plan d'exécution initial choisi plus ou moins aléatoirement, par exemple celui résultant de la compilation directe de la requête utilisateur. Ensuite, seuls les déplacements descendants sont acceptés. C'est l'optimisation locale. Quand le minimum local est atteint, l'algorithme génère au hasard un nouveau plan, et recommence l'optimisation locale à partir de ce nouveau plan. Le processus est répété jusqu'à atteindre une condition d'arrêt, par exemple l'épuisement du temps d'optimisation. Le minimum global est le meilleur minimum local trouvé lors de l'arrêt. L'algorithme est donné en pseudocode figure XIV.18.
Notion XIV.13 : Amélioration itérative (Itérative improvment)
Technique d'optimisation consistant à choisir aléatoirement des plans dans l'espace de recherche, à les optimiser localement au maximum, et enfin à retenir le meilleur des minima locaux comme plan optimal.
Procedure II(Question) {
p = Initial(Question); // générer un plan initial
PlanOptimal = p; // Initialiser le plan optimal
while not(condition_arrêt) do { // Boucle d'optimisation globale
while not (condition_locale) do { // Boucle d'optimisation locale
p' = déplacer(p); // Appliquer une transformation valide à p
if (Coût(p')<Coût(p)) then p = p'; // Garder si moins coûteux
}
// Sélectionner le plan optimal
if coût(p)<coût(PlanOptimal) then PlanOptimal = p;
p = Random(p); // Se déplacer au hasard vers un autre plan
}
Return(PlanOptimal);
}XIX-7-3. LE RECUIT SIMULÉ (SA)▲
Le recuit simulé part également d'un plan initial choisi plus ou moins aléatoirement et génère des plans successifs par application de règles de transformation valide de ce plan. À la différence de l'amélioration itérative, le recuit simulé accepte à la fois des déplacements descendants et montants. L'idée originelle est de simuler le refroidissement d'un métal recuit : tant que le métal est chaud, les mouvements de molécules sont nombreux, puis ils décroissent comme la température. Donc, quand le système est chaud, les déplacements montants qui détériorent le coût du plan sont admis afin de permettre une exploration plus large de l'espace autour du plan en cours d'analyse, pour découvrir d'autres minima locaux. Ces déplacements sont permis avec une probabilité qui décroît avec la température : P = e- DeltaCoût/Température. Le paramètre Température représente la température du système. Il décroît au fur et à mesure de l'avancement de l'optimisation, si bien que les mouvements ascendants sont acceptés avec une probabilité de plus en plus faible. DeltaCoût est la différence de coût entre les deux plans. Quand la condition d'arrêt est atteinte (temps épuisé), le meilleur plan traversé est sélectionné et retenu comme pseudooptimal. La figure XIV.19 donne la procédure correspondante en pseudocode.
Notion XIV.14 : Recuit simulé (Simulated Annealing)
Technique d'optimisation consistant à choisir aléatoirement un plan dans l'espace de recherche et à explorer alentour par des déplacements descendants ou ascendants, ces derniers étant acceptés avec une probabilité qui tend vers 0 quand la température tend vers 0.
Procédure SA(Question) {
p = Initial(Question); // générer un plan initial
PlanOptimal = p; // Initialiser le plan optimal
T = T0; // Initialiser la température
while not(condition_arrêt) do { // Boucle d'optimisation globale
while not(equilibrium) do { // Boucle d'optimisation locale
p' = déplacer(p); // Appliquer une transformation valide à p
delta = cost(p')-cost(p); // Calculer la différence de coût
if (delta<0) then p = p'; // Si coût réduit prendre le nouveau plan
// Si coût accru, accepté si chaud
if (delta>0) then p = p' with probability e- delta/T;
// Maintenir le plan optimal
if cost(p)<cost(PlanOptimal) then PlanOptimal = p;
}
T = reduce(T); // Réduire la température
}
Return(PlanOptimal);
}XIX-7-4. L'OPTIMISATION DEUX PHASES (TP)▲
L'amélioration itérative travaille efficacement pour couvrir de grands espaces et trouver rapidement des minima locaux. Elle ne garantit guère une couverture fine autour de ces minima. Le recuit simulé est bien adapté pour explorer autour d'un minimum local. D'où l'idée de combiner les deux [Ioannidis90], ce qui conduit à l'optimisation deux phases. Tout d'abord, une phase amélioration itérative (II) est exécutée pour trouver les états initiaux de la phase recuit simulé (SA) suivante. Ainsi, l'optimisation deux phases travaille comme suit [Steinbrunn97] :
- Pour un petit nombre de plans aléatoirement sélectionnés, des minima locaux sont cherchés en appliquant II, puis
- À partir du (ou des) moins coûteux de ces minima locaux, SA est appliqué afin d'explorer le voisinage pour trouver de meilleures solutions.
Cette méthode mixte peut donner de bons résultats à condition de bien régler les différents paramètres (temps de chaque phase, température).
XIX-7-5. LA RECHERCHE TABOUE (TS)▲
La recherche taboue (TS) est une procédure du type métaheuristique très efficace pour l'optimisation globale [Glover89]. L'idée principale est de faire à chaque pas le meilleur déplacement possible, tout en évitant une liste de plans tabous. L'utilisation d'une liste de tabous permet d'éviter des recherches inutiles et de converger plus vite vers des solutions proches de l'optimal. TS part d'un plan initial généré aléatoirement, et accomplit les meilleurs mouvements non interdits successivement. À chaque itération, la procédure génère un sous-ensemble V* de l'ensemble des voisins non interdits du plan courant. Le sous-ensemble ne contient donc pas de plans de la liste des tabous. Les plans déjà explorés sont généralement retenus, au moins pour un temps, dans la liste des tabous, ce qui évite en général de boucler. La liste des tabous est mise à jour chaque fois qu'un nouveau plan est exploré pour mémoriser les plans déjà vus. La figure XIV.20 donne le pseudocode correspondant à cet algorithme.
Notion XIV.15 : Recherche taboue (Tabou search)
Technique d'optimisation consistant à se déplacer alentour vers le plan de coût minimal tout en évitant une liste de plans interdits dynamiquement mise à jour.
Procedure TS(Question) {
p = Initial(Question); // générer un plan initial
PlanOptimal = p; // Initialiser le plan optimal
T = φ; // initialiser la liste taboue
while not(condition_arrêt) do { // boucle globale
// accepter tous les mouvements non tabous
générer V*⊆N(p)-T en appliquant déplacer(p);
choisir le meilleur plan p ∈ V*; // Prendre le meilleur plan
T = (T-(plus vieux))∪{p}; // Mettre à jour la taboue liste
// maintenir le plan optimal
if coût(p)<coût(PlanOptimal) then PlanOptimal = p;
}
return(PlanOptimal);
}XIX-7-6. ANALYSE INFORMELLE DE CES ALGORITHMES▲
La performance de tous les algorithmes précédents dépend fortement de la distribution de la fonction de coût sur l'espace de recherche. Alors que le recuit simulé (SA) et la recherche taboue (TS) dépendent fortement du plan initial, l'amélioration itérative (II) et l'optimisation deux phases (TP) utilisent une transformation aléatoire pour explorer cet espace. Pour améliorer les performances de ces algorithmes, des méthodes de transformation d'arbres introduisant une meilleure couverture de l'espace de recherche ont été mises au point. Ce sont par exemple l'échange de jointures et le swap [Swami89, Lanzelotte93]. L'échange de jointure permute aléatoirement des relations alors que le swap échange des parties d'arbres. De telles méthodes ont été introduites seulement pour les jointures relationnelles. Il est possible de les étendre au cas objet.
Suite aux mouvements ascendants, SA est généralement plus lente que les autres méthodes, mais trouve souvent de meilleurs plans que II quand le temps de recherche est suffisant. TP combine les avantages de SA et II. Il a été montré [Ioannidis90] que TP trouve en général de meilleurs plans que SA et II. TS est rapide, mais accomplit une recherche agressive. En conséquence, l'algorithme peut rester bloqué sur un minimum local. Ceci peut être évité avec une longue liste taboue, mais la recherche ralentit alors l'algorithme.
II, SA, TP et TS utilisent tous une fonction appelée déplacer. Celle-ci applique l'une des règles de transformation pour trouver un plan équivalent. Comme vu ci-dessus, dans une base de données objet ou objet-relationnelle avec beaucoup de types, le nombre de règles peut être important. Certaines ne provoquent que de petits déplacements dans l'espace des plans, d'autres de beaucoup plus larges. Il faudrait donc pouvoir introduire des transformations permettant d'appliquer des séquences de règles, et donc de faire de grands sauts dans l'espace des plans. Nous allons étudier une méthode permettant de telles transformations dans la section suivante.
XIX-8. UN ALGORITHME D'OPTIMISATION GÉNÉTIQUE▲
Dans cette section, nous étudions l'approche génétique et son application possible à l'optimisation de requêtes [Bennett91]. Pour l'illustrer concrètement, nous étudions le cas de longues expressions de chemins avec prédicats. Les expressions de chemins sont importantes dans les BD objet ; certains SGBD se concentrent d'ailleurs sur leur optimisation et ne proposent guère d'autres optimisations.
XIX-8-1. PRINCIPE D'UN ALGORITHME GÉNÉTIQUE▲
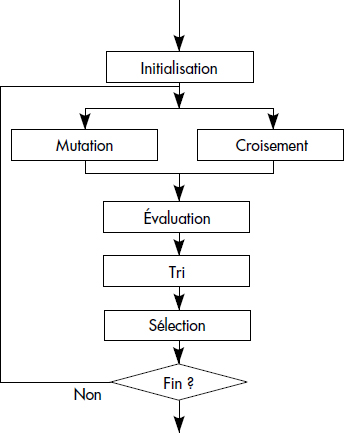
L'algorithme génétique (GA) est un algorithme d'optimisation basé sur les principes d'évolution des organismes dans la nature : l'algorithme cherche à générer les meilleurs éléments d'une population en combinant les meilleurs gènes ensemble. C'est une famille d'algorithmes utilisés dans la recherche d'extrêmes (minimum ou maximum) de fonctions à plusieurs variables [Holland75, Goldberg89]. Ces fonctions sont généralement définies sur des domaines discrets vastes et complexes. Dans notre cas, il s'agit de retrouver idéalement le minimum global de la fonction de coût dans l'espace des plans. Au lieu de travailler sur une solution particulière à chaque étape, l'algorithme considère une population de solutions. Diverses sortes d'algorithmes génétiques ont été proposées pour différentes tâches d'optimisation. La figure XIV.21 représente un algorithme type utilisable pour la recherche du meilleur plan.
Voici les fonctions des principaux blocs d'un tel algorithme :
- Initialisation génère une petite population initiale de solutions (dans notre cas, des plans d'exécution) couvant l'espace de recherche.
- Mutation choisit une solution (c'est-à-dire un plan) de la population, et lui applique des règles de transformation.
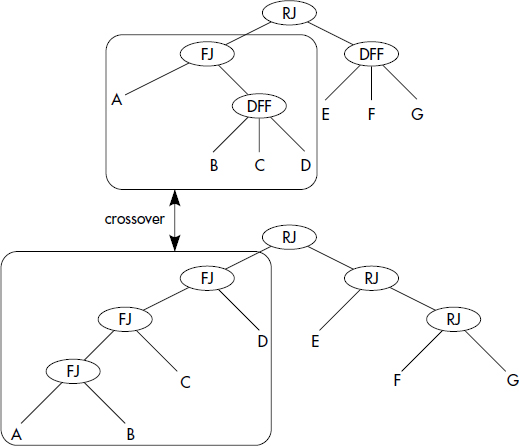
- Croisement choisit deux solutions dans la population et échange leurs gènes communs (dans notre cas, des sous-arbres équivalents) pour générer deux nouvelles solutions.
- Évaluation évalue, pour chaque solution, la fonction à optimiser, dans notre cas la fonction de coût.
- Tri trie la population en fonction du coût.
- Sélection choisit un certain nombre des meilleurs éléments comme parents pour la prochaine génération.
- Fin test le critère d'arrêt afin de stopper l'optimisation.
Le cœur de l'algorithme est la génération d'une nouvelle population par les opérateurs de mutation et de croisement. À chaque génération, une partie de la population subit la mutation et l'autre le croisement. La mutation est identique au déplacement des algorithmes vus ci-dessus. Ce qui est nouveau, c'est le croisement qui permet de construire une solution à partir de deux solutions. Avec la sélection naturelle, il est permis de penser que le croisement ne laissera se propager que les bons gènes, pour converger vers les bons plans. En résumé, la notion d'algorithme génétique peut être définie comme suit :
Notion XIV.16 : Algorithme génétique (Genetic algorithm)
Algorithme de recherche d'optimum consistant à partir d'une population et à la faire se reproduire par mutation et croisement, en sélectionnant les meilleurs éléments à chaque génération, de sorte à converger vers une population contenant la solution optimale ou presque.
XIX-8-2. BASES DE GÈNES ET POPULATION INITIALE▲
Nous appliquons maintenant l'algorithme génétique à l'optimisation des expressions de chemins. Comme vu ci-dessus, différentes méthodes de jointures peuvent être appliquées : la jointure n-aire DFF en profondeur d'abord, la jointure binaire en largeur d'abord notée FJ (plusieurs jointures peuvent être exécutées successivement, ce qui donne l'algorithme BFF), la jointure en arrière notée RJ, et la traversée d'un index de chemins lorsqu'il en existe un, notée PI. Toutes ces méthodes apparaissent comme des gènes permettant de générer la population des plans. La figure XIV.22figure XIV.22 représente la base de gènes avec cinq collections liées par une chaîne d'association. S'il n'y a ni lien inverse, ni index de chemin, le nombre total de gènes est le nombre de cellules dans le triangle supérieur de la généralisée à n, soit :
Genes = Σ 1 + 2 + … + (n - 1) + 2 * (n - 1) = (n2 + 3 * n - 2)/2Dans tous les cas, le nombre de gènes est de l'ordre de O(n2). Un plan d'exécution peut être vu comme une combinaison de gènes dont le résultat permet le parcours du chemin, dans un sens ou dans l'autre, ceci afin de trouver le résultat de la requête. L'objectif de l'optimiseur est de trouver la meilleure combinaison de gènes pour obtenir le plan de coût minimal.
L'étape d'initialisation consiste à générer aléatoirement une population initiale de plans. Notons qu'une telle population est générée par des parcours aléatoires dans la base de gènes de la figure XIV.22, depuis la collection source jusqu'à la collection cible. De tels parcours évitent les produits cartésiens, ce qui est généralement sage.
XIX-8-3. OPÉRATEUR DE MUTATION▲
La mutation est un des opérateurs importants d'une méthode génétique. À chaque étape, un certain pourcentage des plans doit subir une mutation. Cette procédure consiste simplement à sélectionner un sous-arbre et à lui appliquer une règle de transformation valide. Quelques exemples de mutation possibles sont représentés figure XIV.23. La mutation apporte de nouveaux gènes qui peuvent ne pas exister dans la population courante.
XIX-8-4. OPÉRATEUR DE CROISEMENT▲
Cet opérateur consiste à mixer deux éléments de la population pris plus ou moins au hasard. Par exemple, deux plans sont choisis et leurs sous-arbres communs sont échangés. Deux sous-arbres sont équivalents s'ils ont les mêmes feuilles et génèrent les mêmes résultats. La figure XIV.24 illustre un croisement. Alors que la mutation transforme un plan en l'un de ses voisins, en accomplissant de petits mouvements, le croisement peut accomplir de plus larges transformations. Il permet ainsi de sortir de zone voisine d'un minimum local, en sautant vers une autre partie de l'espace de recherche.
La figure XIV.25 donne le pseudocode de l'algorithme génétique appliqué à l'optimisation des expressions de chemins. Nous utilisons le tableau Popu pour représenter la population. Chaque élément contient deux variables : un plan et son coût. BasePopu contient les plans subissant le croisement ou la mutation. Comme la population s'accroît après le croisement, la procédure de sélection est appliquée avant de passer à la nouvelle génération. Celle-ci conserve les plans de coûts minimaux. Pendant le croisement, le plus grand sous-arbre commun des deux parents est choisi. Si deux parents n'ont pas de sous-arbre commun, ils sont soumis à la mutation. Les plans résultants du croisement sont placés de BasePopu + 1 à NewPopu. Part est le pourcentage de la population effectuant un croisement.
Procedure GA(Question) {
Générer(Popu[BasePopu]) ; // Initialiser la population aléatoirement
Sort(Popu) ; // Trier la population des plans par coût croissant
PlanOptimal = Popu[0] ; // Garder le meilleur plan trouvé
While not (condition_arrêt) do {
Pourcent = 0;
While Pourcent < Part * BasePopu do {
// Appliquer croisement à Part de la population
p1 = Popu[Random(BasePopu)] ; // Choisir p1 et p2 de Popu
p2 = Popu[Random(BasePopu)] ; // aléatoirement
Croisement(p1, p2) ; // Les croiser si possible
Pourcent = Pourcent + 2 ;
}
For le reste de Popu do Mutation ; // Mutation pour les autres
For (i=0 ; i < NewPopu ; i++) do evaluate(Popu[i]) ; // Calcul du coût
Trier(Popu) ; // Trier la population par coût croissant
PlanOptimal = Popu[0] ; // Garder le meilleur plan trouvé
}
return(PlanOptimal) ;
}Des expériences effectuées avec cet algorithme ont montré qu'il pouvait être amélioré en ajoutant des plans aléatoirement générés à chaque génération, ceci afin de garantir la diversité des plans explorés [Tang96]. Les limites de tels algorithmes d'optimisation appliqués aux bases de données, notamment dans le cas d'un très grand nombre de règles, restent encore à découvrir.
XIX-9. CONCLUSION▲
Dans ce chapitre, nous avons étudié différentes techniques d'optimisation pour les SGBD objet. Tout d'abord, les techniques de groupage des objets sur disques permettent de placer à proximité les objets souvent accédés ensemble, par exemple via des parcours de chemins. Elles prolongent les techniques de groupage des relations par jointures précalculées de certains SGBD relationnels. Au-delà, les index de chemins constituent aussi une spécificité des BD objet ; ils peuvent être perçus comme une extension des index de jointure des BD relationnelles.
Ensuite, nous avons étudié différents algorithmes de parcours de chemins. Ces algorithmes permettent la navigation ensembliste dans les BD objet. Ils sont des extensions naturelles des algorithmes de jointures [Valduriez87], qu'ils étendent en utilisant des identifiants d'objets.
La génération de plans équivalents est plus complexe que dans le cas relationnel, surtout par la nécessité de prendre en compte les types de données utilisateurs et les réécritures d'expressions de méthodes associées. Ceci nécessite le développement d'optimiseurs extensibles, supportant l'ajout de règles de réécriture. Ce sont de véritables systèmes experts en optimisation, qui sont maintenant au cœur des SGBD objet-relationnels.
Le développement d'un modèle de coût pour bases de données objet est un problème des plus difficiles. Il faut prendre en compte de nombreuses statistiques, les groupes, les références, les index de chemins, les méthodes et les différentes formes de collections. Nous avons présenté un modèle de coût simple élaboré par extension des modèles classiques des BD relationnelles. Peu d'optimiseurs prennent en compte un modèle de coût intégrant les spécificités de l'objet, par exemple les méthodes. Beaucoup reste à faire.
Nous avons enfin développé des stratégies de recherche sophistiquées pour trouver le meilleur plan d'exécution. Plusieurs ont été proposées et paraissent suffisantes pour des questions mettant en jeu une dizaine de collections. Au-delà, les stratégies génétiques semblent prometteuses. Peu de SGBD utilisent aujourd'hui ces stratégies, la plupart restant basés sur la programmation dynamique. L'intégration dans des systèmes pratiques reste donc à faire.
XIX-10. BIBLIOGRAPHIE▲
[Amsaleg93] Amsaleg L., Gruber O., « Object Grouping in EOS », Distributed Object Management, Morgan Kaufman Pub., San Mateo, CA, p. 117-131, 1993.
- EOS est un gérant d'objets à un seul niveau de mémoire réalisé à l'INRIA de 1990 à 1995. Une technique originale de groupement d'objets avec priorité a été proposée, ainsi que des techniques de ramassage de miettes.
[Bertino89] Bertino E., Kim W., « Indexing Techniques for Queries on Nested Objects », IEEE Transactions on Knowledge and Data Engineering, vol. 1(2), June 1989, p. 196-214.
- Cet article compare différentes techniques d'indexation pour les bases de données objet, en particulier plusieurs techniques d'index de chemins et d'index séparés ou groupés (multiindex) dans le cas de hiérarchie de généralisation.
[Bertino91] Bertino E., « An Indexing Technique for Object-Oriented Databases », Proceedings of Int. Conf. Data Engineering, Kobe, Japan, p. 160-170, April 1991.
- Cet article développe le précédent et propose des techniques de recherche et mise à jour avec index de chemin.
[Bertino92] Bertino E., Foscoli P., « An Analytical Model of Object-Oriented Query Costs », Persistent Object Systems, Workshop in Computing Series, Springer-Verlag, 1992.
- Les auteurs développent un modèle de coût analytique pour BD objet. Celui-ci prend notamment en compte les index de chemin.
[Bennett91] Bennett K., Ferris M.C., Ioannidis Y.E., « A Genetic Algorithm for Database Query Optimization », Proc. 4th International Conference on Genetic Algorithms, San Diego, CA, p. 400-407, June 1991.
- Cet article a proposé pour la première fois l'utilisation d'un algorithme génétique dans les bases de données objet.
[Christophides96] Christophides V., Cluet S., Moerkotte G., « Evaluating Queries with Generalized Path Expressions », Proceedings of the 1996 ACM SIGMOD International Conference on Management of Data, ACM Ed., 1996.
- Cet article propose d'étendre OQL avec des expressions de chemin généralisées, par exemple traversant de multiples associations. Des techniques d'évaluation de telles expressions de chemin sont discutées. Il est montré comment ces techniques peuvent être intégrées dans le processus d'optimisation.
[Cluet92] Cluet S., Delobel C., « A General framework for the Optimization of Object-Oriented Queries », Proceedings of the 1992 ACM SIGMOD International Conference on Management of Data, ACM Ed., p. 383-392, 1992.
- Cet article développe un cadre général pour l'optimisation de requêtes objet basé sur la réécriture de graphes d'opérations. Il étend la réécriture d'expressions algébriques en introduisant une sorte de graphe de flux. Les nœuds représentent les collections et les arcs les opérations. Des informations de typage sont ajoutées aux nœuds. La réécriture des expressions de chemins est intégrée à la réécriture des expressions algébriques. Les index et le groupage sont aussi pris en compte.
[Cluet94] Cluet S., Moerkotte G., « Classification and Optimization of Nested Queries xin Object bases », Journées Bases de Données Avancées, 1994.
- Cet article contient une classification des requêtes imbriquées en OQL. Il propose des techniques de désimbrication basées sur la réécriture algébrique.
[DeWitt93] DeWitt D., Lieuwen D., Mehta M., « Pointer-based join techniques for object-oriented databases », Proceedings of Parallel and Distributed System International Conf., San Diego, p. 172-181, CA, 1993.
- Les auteurs comparent divers algorithmes de traversées de chemin dans les bases de données objet. Ils comparent leurs performances et étudient la parallélisation.
[Finance94] Finance B., Gardarin G., « A Rule-Based Query Optimizer with Multiple Search Strategies, Data & Knowledge Engineering Journal, North-Holland Ed., vol. 13, n° 1, p. 1-29, 1994.
- Un article proposant un optimiseur extensible pour bases de données à objets : l'optimiseur est basé sur des règles de transformations d'arbres d'opérations algébriques, exprimées sous la forme de règles de réécriture de termes. Les restructurations incluent des règles syntaxiques (descente des opérations de filtrages, permutation des jointures) et sémantiques (prises en compte de contraintes d'intégrité). La stratégie de recherche est elle-même paramétrable par des règles. Un tel optimiseur a été implémenté dans le projet Esprit EDS.
[Florescu96] Florescu D., « Espaces de Recherche pour l'Optimisation des Requêtes Orientées Objets », Thèses de Doctorat, Université de Paris VI, Versailles, 1996.
- Cette excellente thèse de doctorat décrit la conception et la réalisation d'un optimiseur extensible pour bases de données objet. Les règles de réécriture sont introduites par des équivalences de requêtes. Ceci permet de traiter des cas variés, comme les ordonnancements de jointures, les réécritures de chemins, la prise en compte de règles sémantiques et de vues concrètes, etc. L'optimiseur est capable d'appliquer différentes stratégies de recherche à différents niveaux.
[Gardarin95] Gardarin G., Gruser J.R., Tang Z.H., « A Cost Model for Clustered Object-Oriented Databases », Proceedings of 21st International Conference on Very Large Databases, Zurich, Switzerland, 1995, p. 323-334.
- Cet article présente les techniques de groupage avec priorité et le modèle de coût pour BD objet décrits ci-dessus.
[Gardarin96] Gardarin G., Gruser J.R., Tang Z.H., « Cost-based Selection of Path Expression Processing Algorithms in Object-Oriented Databases », Proceedings of the 22nd International Conference on Very Large Data Bases, Bombay, India, 1996, p. 390-401.
- Cet article détaille les principaux algorithmes d'expression de chemins présentés ci-dessus, étudie leur coût et propose des heuristiques permettant de choisir le meilleur algorithme.
[Glover89] Glover F., « Tabu Search-part I », ORSA Joinal on Computing 1, p. 190-206, 1989.
[Glover90] Glover F., « Tabu Search-part II », ORSA Joinal on Computing 2, p. 4 -32, 1990.
- Deux articles de référence qui développent les techniques taboues de recherche.
[Goldberg89] Goldberg D. E., Genetic Algorithms in Search Optimization and Machine Learning, Addison-Wesley, Reading, MA, 1989.
- Ce livre décrit des stratégies de recherche d'optimum, notamment pour l'apprentissage. Une place importante est réservée aux algorithmes génétiques.
[Graefe93] Graefe G., McKenna W., « The Volcano Optimizer Generator », Proceedings of the 9th International Conference on Data Engineering, IEEE Ed., p. 209-218, 1993.
- Cet article décrit l'optimiseur extensible Volcano, basé sur des règles de réécriture dont les conditions et les actions sont écrites comme des procédures C. Volcano supporte l'optimisation de plans pour architecture parallèle.
[Haas89] Haas L. M., Cody W.F., Freytag J.C., Lapis G., Lindsay B.G., Lohman G.M., Ono K., Pirahesh H., « Extensible Query Processing in Starburst », Proceedings of the 1989 ACM SIGMOD International Conf. on Management of Data, ACM Ed., p. 377-388, 1989.
- Starburst fut le projet de recherche qui a permis le développement des techniques objet-relationnelles chez IBM. L'optimiseur extensible fut un des premiers réalisés. Il distinguait la phase de réécriture de celle de planning. La première était paramétrée par des règles, la seconde par des tables d'opérateurs.
[Harris96] E.P. Harris, K. Ramamohanarao, « Join Algorithm Costs Revisited », The VLDB Journal, vol. 5(1), p. 64-84,1996.
- Cet article propose différents algorithmes de jointures et compare très précisément les coûts en entrées-sorties et en temps unité centrale.
[Hellerstein93] Hellerstein J. M., Michael Stonebraker, » Predicate Migration: Optimizing Queries with Expensive Predicates », ACM SIGMOD Intl. Conf. On Management of Data, p. 267-276, 1993.
- Cet article discute de l'optimisation de questions avec des prédicats coûteux, incluant des fonctions utilisateur. Il propose des méthodes de transformation.
[Holland75] Holland J.H., Adaptation in Natural and Artificial Systems, University of Michigan Press, Ann Arbor, MI, 1975.
- Ce livre traite de l'adaptation et introduit en particulier les algorithmes génétiques pour des fonctions multivariables.
[Ioannidis87] Ioannidis Y.E.,Wong E., « Query Optimization by Simulated Annealing », Proceedings of the 1987 ACM SIGMOD Conference on Management of Data, San Francisco, California, p. 9-22,1987.
- Cet article présente l'adaptation de la stratégie de recherche « recuit simulé » à l'optimisation de requêtes Select-Project-Join. La méthode est évaluée en comparaison à la programmation dynamique classique.
[Ioannidis90] Ioannidis Y., Kang Y.C., « Randomized Algorithms for Optimizing Large Join Queries », Proceedings of the 1990 ACM SIGMOD Intl. Conference on Management of Data, Atlantic City, NJ, p. 312-321, 1990.
- Cet article présente l'adaptation des stratégies de recherche amélioration itérative et recuit simulé à l'optimisation de requêtes Select-Project-Join. Il teste ces algorithmes sur de larges requêtes et montre que le recuit simulé trouve en général un meilleur plan. La méthode deux phases est alors proposée pour corriger l'amélioration itérative. Il est finalement montré que cette méthode est la meilleure des trois.
[Ioannidis91] Ioannidis Y., Kang Y.C., « Left-Deep vs. Bushy Trees : An Analysis of Strategy Spaces and its Implications for Query Optimization », Proceedings of the 1991 ACM SIGMOD International Conference on Management of Data, Denver, Colorado, 1991, p. 168-177.
- Cet article étudie les stratégies d'optimisation en fonction de l'espace de recherche considéré : espace limité aux arbres linéaires gauches ou prenant en compte tous les arbres, y compris les arbres branchus.
[Kim89] Kim K.C., Kim W., Dale A., « Indexing Techniques for Object-Oriented Databases », Object-oriented concepts, Databases, and Applications, W. Kim and F. H. Lochovsky, editors, AddisonWesley, 1989, p. 371-392.
- Cet article introduit et évalue les index de chemins.
[Kemper90] Kemper A., Moerkotte G., « Advanced Query Processing in Object Bases Using Access Support Relations », Proceedings of the 16th International Conference on Very Large Data Bases, Brisbane, Queensland, Australia, p. 290-301, 1990.
- Cet article décrit l'optimiseur de GOM (Generic Object Model), un prototype réalisé à Karlsruhe. Cet optimiseur utilise des index de chemins sous la forme de relations support et un optimiseur basé sur des règles de réécriture. Ces dernières permettent l'intégration des index dans le processus de réécriture.
[Lanzelotte91] Lanzelotte R., Valduriez P., « Extending the Search Strategy in a Query Optimizer », 17th International Conference on Very Large Data Bases, Barcelona, Catalonia, Spain, Morgan Kaufman Pub, p. 363-373,1991.
- Cet article montre comment une conception orientée objet permet de rendre extensible un optimiseur pour bases de données. Plus particulièrement, la stratégie de recherche peut être paramétrée et changée en surchargeant quelques méthodes de base. Les stratégies aléatoires (amélioration itérative, recuit simulé, algorithmes génétiques) sont particulièrement intégrables à l'optimiseur.
[Lanzelotte93] Lanzelotte R., Valduriez P., Zait, M. « On the Effectiveness of Optimization Search Strategies for Parallel Execution Spaces », Proceedings of the 19th International Conference on Very Large Data Bases, Dublin, Ireland, p. 493-504, 1993.
- Cet article analyse différentes stratégies d'optimisation pour l'optimisation de requêtes parallèles.
[Mitchell93] Mitchell G., Dayal U., Zdonick S., « Control of an Extensible Query Optimizer : A Planning-Based Approach », Proceedings of the 19th International Conference on Very Large Data Bases, Dublin, Ireland, p. 517-528,1993.
- Les auteurs proposent d'organiser un optimiseur en modules de connaissance appelés régions, chaque région ayant sa propre stratégie de recherche. Les régions sont organisées hiérarchiquement, chaque région parente contrôlant ses subordonnées. Chaque région décrit ses capacités via son interface. Un niveau de contrôle global utilise les capacités des régions afin de planifier une séquence d'exécutions des régions pour traiter une requête. Le contrôle global est un planning dirigé par les buts.
[Nahar86] Nahar S., Sahni S., Shragowitz E., « Simulated Annealing and Combinatorial Optimization », Proceedings of the 23rd ACM/IEEE Design Automation Conference, Las Vegas, NV, p. 293-299, 1986.
- Cet article décrit la technique de recuit simulé pour l'optimisation combinatoire.
[Orenstein92] Orenstein J., Haradhvala S., Margulies B., Sakahara D., « Query Processing in the ObjectStore Database System », ACM SIGMOD Int. Conf. on Management of Data, San Diego, Ca., 1992.
- ObjectStore est un SGBD objet parmi les plus vendus. Il supporte la persistance des objets C++ de manière orthogonale aux types de données, la gestion de transactions et les questions associatives. Il est basé sur une technique efficace de gestion de mémoire virtuelle intégrée au système. Les collections sont gérées comme des objets. Les questions sont intégrées à C++ sous forme d'opérateurs dont les opérandes sont une collection et un prédicat. Le prédicat peut lui-même contenir une question imbriquée. Cet article décrit la stratégie d'optimisation de questions implémentées.
[Ozsu95] Ozsu T., Blakeley J.A., « Query Processing in Object-oriented Database Systems », Modern database systems, edited by W. Kim, p. 146-174, 1995.
- Cet article présente une vue d'ensemble des techniques d'optimisation dans les BD objet : architecture, techniques algébriques de réécriture, expressions de chemins, exécution des requêtes. C'est un bon tutoriel sur le sujet.
[Shekita89] Shekita E. J., Carey M. J., « A Performance Evaluation of Pointer-Based Joins », Proceddings of the 1990 ACM SIGMOD Intl. Conference on Management of Data, New Jersey, p. 300-311, May 1990.
- Cet article décrit trois algorithmes de jointures basés sur des pointeurs. Ce sont des variantes des boucles imbriquées, du tri-fusion et du hachage hybride. Une analyse permet de comparer ces algorithmes aux algorithmes correspondants qui ne sont pas basés sur des pointeurs. Il est montré que l'algorithme naturel de traversée en profondeur est peu efficace.
[Steinbrunn97] Steinbrunn M., Moerkotte G., Kemper A., « Heuristic and Randomized Optimization for the Join Ordering Problem », VLDB Journal, p. 191-208, 1997.
- Les auteurs présentent une description assez complète et une évaluation comparée de tous les algorithmes d'optimisation combinatoire proposés pour les bases de données.
[Swami88] Swami A. N., Gupta A., « Optimization of Large Join Queries », Proceedings of the 1988 ACM SIGMOD Intl. Conference on Management of Data, Chicago, Illinois, p. 8-17,1988.
- Il s'agit du premier article ayant introduit les techniques d'optimisation aléatoire pour chercher le meilleur plan d'exécution. Les auteurs montrent que le problème de recherche du meilleur plan est NP complet. Les méthodes combinatoires d'optimisation telles que l'itération itérative et le recuit simulé sont alors proposées. Des comparaisons montrent l'intérêt de l'amélioration itérative.
[Swami89] Swami A. N., « Optimization of Large Join Queries : Combining Heuristics and Combinatorial Techniques », Proceedings of the 1989 ACM SIGMOD Conference, Portland, Oregon, 1989, p. 367-376.
- Les auteurs discutent la combinaison d'algorithmes combinatoires tels que l'amélioration itérative et le recuit simulé avec des heuristiques d'optimisation comme l'augmentation, l'amélioration locale et KBZ. L'augmentation consiste à choisir les relations dans un certain ordre croissant selon une mesure simple - la taille, la taille du résultat attendu, la sélectivité, le nombre de relations joignant, etc. L'heuristique KBZ consiste à étudier tous les arbres dérivant d'un arbre choisi en permutant la racine. Ils définissent ainsi différents algorithmes combinés qui sont comparés. Les résultats sont encourageants pour la combinaison de l'amélioration itérative avec l'augmentation.
[Tan91] Tan K-L., Lu H., « A Note on the Strategy Space of Multiway Join Query Optimization Problem in Parallel Systems », ACM SIGMOD Record, vol. 20, 1991, p. 81-82.
- Les auteurs étudient l'espace de recherche pour un arbre de jointure quelconque dans le cas d'un système parallèle. Ils estiment en particulier sa taille.
[Tang96] Tang Z., « Optimisation de requêtes avec expressions de chemin pour BD objet », Thèse de doctorat, Université de Versailles, 197 pages, Versailles, France, sept. 1996.
- Cette thèse développe et compare trois algorithmes de traversée de chemins. L'auteur discute leur intégration dans le processus d'optimisation. Une stratégie génétique est proposée pour choisir la meilleure traversée pour de longs chemins. Diverses comparaisons démontrent l'intérêt de cette méthode. Un modèle de coût pour BD objet voisin du modèle décrit ci-dessus est développé, avec la formule de Tang.
[Valduriez87] Valduriez P., « Optimization of Complex Database Queries Using Join Indices », Database Engineering Bulletin, vol. 9, 1986, p. 10-16.
- Cet article introduit les index de jointures, précurseurs des index de chemins.
[Vance96] Vance B., Maier D., « Rapid Bushy Join-order Optimization with Cartesian Products », Proceedings of the 1996 ACM SIGMOD Conference on Management of Data, Montreal, Canada, p. 35-46, 1996.
- Cet article montre qu'il est possible d'implémenter avec les techniques actuelles un optimiseur capable de considérer tous les arbres de jointures, y compris ceux avec des produits cartésiens.
[Yao77] Yao S.B., « Approximating the Number of Accesses in Database Organizations », Comm. of the ACM, vol. 20, n° 4, p. 260-270, April 1977.
- Cet article introduit la fameuse formule de Yao.