XXII. CONCEPTION DES BASES DE DONNÉES▲
XXII-1. INTRODUCTION▲
Une des tâches essentielles des développeurs de bases de données est la conception du schéma des bases. L'objectif est de structurer le domaine d'application de sorte à le représenter sous forme de types et de tables. La représentation doit être juste pour éviter les erreurs sémantiques, notamment dans les réponses aux requêtes. Elle doit aussi être complète pour permettre le développement des programmes d'application souhaités. Elle doit enfin être évolutive afin de supporter la prise en compte rapide de nouvelles demandes.
Le concepteur, ou plutôt l'administrateur de base, effectue également le choix du placement des tables sur disques et le choix des index, choix essentiels pour les performances. En exagérant un peu, on peut dire qu'il n'y a pas de mauvais SGBD, mais de mauvais concepteurs responsables des erreurs sémantiques ou des mauvaises performances. Les choix de structures physiques sont dépendants des programmes qui manipulent la base, particulièrement des types et fréquences des requêtes d'interrogation et de mise à jour.
Traditionnellement, la démarche de conception s'effectue par abstractions successives, en descendant depuis les problèmes de l'utilisateur vers le SGBD. Nous proposons de distinguer cinq étapes :
- Perception du monde réel et capture des besoins. Cette étape consiste à étudier les problèmes des utilisateurs et à comprendre leurs besoins. Elle comporte des entretiens, des analyses des flux d'information et des processus métier. Des démarches de type BPR (Business Process Reengineering) [Hammer93] de reconception des processus métiers existants en les dirigeant vers le client peuvent être un support pour cette étape. La génération de modèles de problèmes est aussi une technique courante à ce niveau [DeAntonellis83]. Comme il est difficile de comprendre le problème dans son ensemble, les concepteurs réalisent des études de cas partiels. Le résultat se compose donc d'un ensemble de vues ou schémas externes qu'il faut intégrer dans l'étape suivante. Ces vues sont exprimées dans un modèle de type entité-association ou objet, selon la méthode choisie.
- Élaboration du schéma conceptuel. Cette étape est basée sur l'intégration des schémas externes obtenus à l'étape précédente. Chaque composant est un schéma entité-association ou objet. Il résulte d'un modèle de problème représentant une partie de l'application. La difficulté est d'intégrer toutes les parties dans un schéma conceptuel global complet, non redondant et cohérent. Des allers et retours avec l'étape précédente sont souvent nécessaires.
- Conception du schéma logique. Cette étape réalise la transformation du schéma conceptuel en structures de données supportées par le système choisi. Avec un SGBD relationnel, il s'agit de passer à des tables. Avec un SGBD objet-relationnel, il est possible de générer des types et des tables, les types étant réutilisables. Avec un SGBD objet, il s'agit de générer des classes et des associations. Cette étape peut être complètement automatisée, comme nous le verrons.
- Affinement du schéma logique. Une question qui se pose est de savoir si le schéma logique obtenu est un « bon » schéma. À titre de première approximation, un « bon schéma » est un schéma sans oublis ni redondances d'informations. Pour caractériser plus précisément les « bons » schémas, le modèle relationnel s'appuie sur la théorie de la normalisation, qui peut être avantageusement appliquée à ce niveau. En relationnel, l'objectif est de grouper ou décomposer les tables de manière à représenter fidèlement le monde réel modélisé.
- Élaboration du schéma physique. Cette étape est nécessaire pour obtenir de bonnes performances. Elle nécessite la prise en compte des transactions afin de déterminer les patterns d'accès fréquents. À partir de là, il faut choisir les bonnes structures physiques : groupage ou partitionnement de tables, index, etc. C'est là que se jouent pour une bonne part les performances des applications.
Dans ce chapitre, nous étudions essentiellement les étapes 2, 3 et 4 qui font largement partie du domaine des bases de données. La partie 1 appartient plutôt au génie logiciel, voire à l'économie ou la psychologie. Nous ne l'aborderons guère. Nous détaillons surtout la partie 3 où toute une théorie s'est développée à la fin des années 70 et au début des années 80 pour les bases relationnelles.
Dans la section qui suit, nous abordons le problème de la conception du schéma conceptuel. C'est l'occasion de présenter le langage de modélisation UML, plus précisément les constructions nécessaires à la modélisation de BD. Nous discutons aussi des techniques d'intégration de schémas. La section 3 développe les règles pour passer d'un schéma conceptuel UML à un schéma relationnel. Elle propose aussi quelques pistes pour passer à l'objet-relationnel. La section 4 présente les approches pour l'affinement du schéma logique. La théorie de la normalisation, qui peut être intégrée au cœur de l'affinement, est l'objet des trois sections qui suivent. La section 5 discute les principales techniques d'optimisation du schéma physique. Nous concluons en résumant et discutant les voies d'évolution.
XXII-2. ÉLABORATION DU SCHÉMA CONCEPTUEL▲
Dans cette section, nous traitons des techniques permettant de définir un schéma conceptuel. Nous procédons par modélisation entité-association ou objet en construisant des diagrammes basés sur UML, le langage de modélisation unifié standardisé par l'OMG.
XXII-2-1. PERCEPTION DU MONDE RÉEL AVEC E/R▲
Le monde des applications informatiques peut être modélisé à l'aide d'entités qui représentent les objets ayant une existence visible, et d'associations entre ces objets [Benci76, Chen76]. Le modèle entité-association (Entity Relationship, E/R) a eu un très grand succès pour représenter des schémas externes d'un domaine de discours particulier, autrement dit des parties d'une application. Comme nous l'avons vu au chapitre II, ce modèle repose sur des entités encore appelées individus, des associations ou relations entre entités, et des attributs ou propriétés. Il est à la base de Merise [Tardieu83] et de nombreuses autres méthodes. Une entité modélise un objet intéressant perçu dans le réel analysé, ayant une existence propre. Un attribut est une information élémentaire qui caractérise une entité ou une association et dont la valeur dépend de l'entité ou de l'association considérée. Une association est un lien sémantique entre deux entités ou plus. Définir une vue du réel analysé par le modèle entité-association nécessite d'isoler les types d'entités, d'associations et d'attributs.
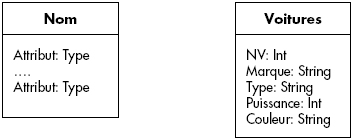
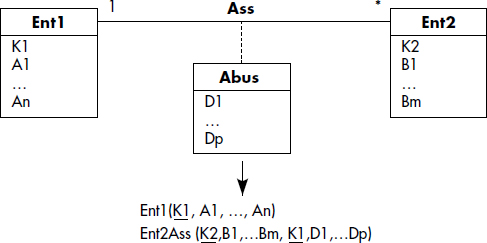
Différents diagrammes ont été introduits pour représenter les schémas entité-association. Au chapitre II, nous avons introduit les notations originelles de Chen. Dans la suite, nous utilisons la représentation proposée dans le langage universel de modélisation UML [Rational98]. En effet, ce langage devient le standard pour la conception dans les entreprises. Poussé par l'OMG, il a le mérite d'être complet, clair et sans doute résistant à l'usure du temps, comme tous les standards. La construction de base dérivée du langage UML pour représenter des entités est symbolisée figure XVII.1. À titre d'exemple, nous avons représenté des voitures avec les attributs numéro de véhicule (NV), marque, type, puissance et couleur.
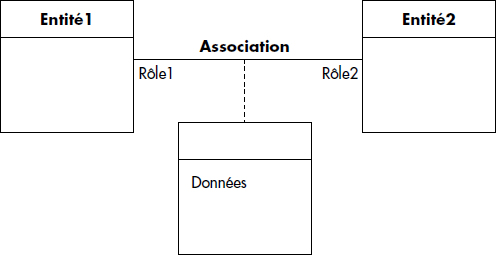
La construction de base permettant de représenter des associations est symbolisée figure XVII.2. Nous représentons là une association binaire générique avec attributs. L'association entre les entités Entité1 et Entité2 est représentée par un trait simple. Le nom de l'association apparaît au-dessus du trait. Les attributs sont représentés par une entité sans nom accrochée par un trait en pointillé à l'association. Si les données participent elles-mêmes à des associations, il est possible de leur donner un nom : on a alors une véritable entité associative possédant une valeur pour chaque instance de l'association binaire. La représentation d'associations ternaires est possible avec UML : on utilise alors un losange où convergent les traits associatifs et de données. Cependant, nous déconseillons l'emploi de telles associations difficiles à lire : les associations n-aires peuvent toujours se représenter par une classe associative en ajoutant une contrainte qui exprime que les associations sont instanciées ensemble. Par exemple, une vente associe simultanément un client, un produit et un vendeur. Dans la suite, nous considérons souvent des associations binaires, plus faciles à manipuler et à comprendre.
Dans une association, chaque entité participante joue un rôle. Celui-ci peut être explicitement nommé, comme indiqué figure XVII.2. Mais ceci n'est pas obligatoire. Les associations sont caractérisées par des cardinalités : la cardinalité [m,n] attachée à une entité indique le nombre minimal et maximal d'instance d'associations pour une instance de cette entité.
Notion XVII.1 : Cardinalités d'association (Relationship cardinalities)
Cardinalités minimale et maximale associées à chacun des rôles de l'association, indiquant le nombre minimal et maximal d'instances d'association auxquelles participe une instance de l'entité du rôle.
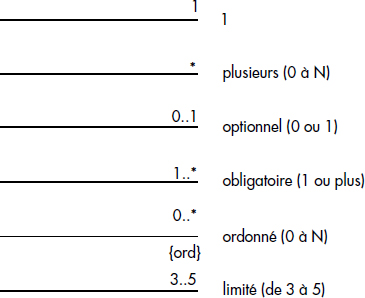
Une cardinalité se lit donc dans le sens entité vers association. Il faut se demander pour une instance d'entité (ou de classe) combien d'instances d'association lui sont attachées ? Avec des associations binaires, cela revient à indiquer le nombre d'instances de l'autre entité pour une instance de celle à laquelle est attachée la cardinalité. UML propose les notations indiquées figure XVII.3 pour les cardinalités. Notez que 1 signifie à la fois un minimum de 1 et un maximum de 1. La notation {ord} signifie que l'ordre d'apparition des entités dans l'association est important.
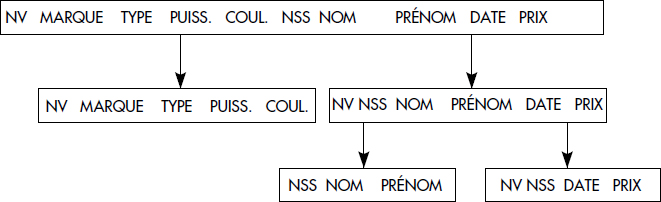
À titre d'exemple, soient une base modélisant des entités « personne » et « voiture », et le type d'association « possède » qui traduit le fait qu'une personne est propriétaire d'une ou plusieurs voitures. Une personne est caractérisée par un numéro de Sécurité Sociale (NSS), un nom, un prénom et une date de naissance alors qu'une voiture est caractérisée par les attributs déjà vus NV, MARQUE, TYPE, PUISSANCE et COULEUR. Chaque personne est identifiée par une occurrence du numéro de Sécurité Sociale (NSS), alors que chaque voiture est identifiée par un numéro de véhicule (NV). À chaque occurrence d'association correspond par exemple une date d'achat (DATE) et un prix d'achat (PRIX). La figure XVII.4 représente le schéma externe correspondant décrit avec les notations UML réduites aux entités, associations et attributs. Les cardinalités indiquent qu'une personne peut posséder de O à N voitures alors qu'une voiture est possédée par une et une seule personne.
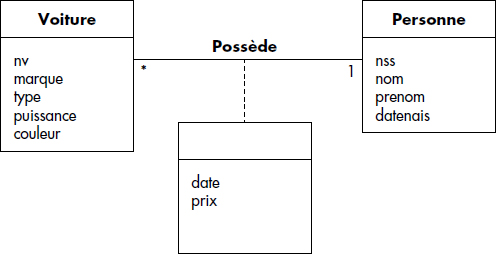
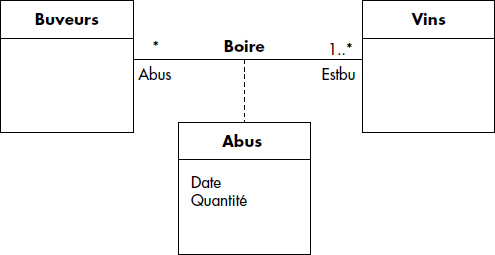
Nous présentons figure XVII.5 l'exemple classique des buveurs, des vins et de l'association boire caractérisée par une date et une quantité. Les cardinalités sont donc portées par les rôles : le rôle Estbu porte la cardinalité 1..*, ce qui signifie qu'à un buveur est associé entre 1 et N abus ou vins si l'on préfère. * est une notation raccourcie pour 0..*. Le rôle Estbu porte cette cardinalité, ce qui signifie qu'un vin est bu par 0 à N buveurs. Tout cela, aux notations près, est bien connu, mais souvent confus, les cardinalités étant interprétées de différentes manières selon les auteurs. Nous avons choisi ces notations pour assurer la compatibilité avec l'approche objet et UML que nous allons maintenant développer un peu plus.
XXII-2-2. PERCEPTION DU MONDE RÉEL AVEC UML▲
UML (Universal Modelling Language) est donc le langage qui se veut universel pour la modélisation objet. Nous l'avons déjà souvent approximativement utilisé pour représenter des objets. UML a été développé en réponse à l'appel à proposition lancé par l'OMG (Object Management Group). Il existe de nombreux ouvrages sur UML et nous nous contenterons des constructions utiles pour modéliser les bases de données. Le lecteur désirant en savoir plus pourra se reporter à [Bouzeghoub97], [Muller98] ou encore [Kettani98]. UML présente beaucoup d'autres diagrammes que ceux utilisés, en particulier pour représenter les cas d'utilisation, les séquences, les transitions d'états, les activités, les composants, etc. Nous utilisons essentiellement les diagrammes de classe, d'association, d'héritage et d'agrégation.
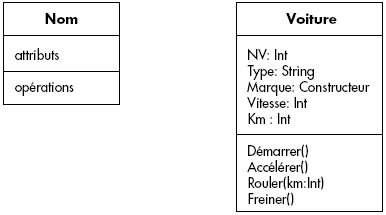
Une classe est une extension du concept d'entité avec des opérations, comme le montre la figure XVII.6. Nous donnons en exemple la classe Voiture avec les opérations Démarrer(), Accélérer(), Rouler() et Freiner(). UML distingue aussi les attributs privés précédés de - et publics notés +. D'autres niveaux de visibilité sont possibles. Pour l'instant, et par défaut, nous supposons tous les attributs publics. Cela n'est pas très conforme à l'objet, mais les spécialistes des bases de données sont des briseurs d'encapsulation bien connus, car ils s'intéressent avant tout aux données !
La découverte des classes, comme celle des entités, nécessite d'isoler les types d'objets du monde réel qui ont un cycle de vie propre. Dans une description en langage naturel, les classes comme les entités correspondent souvent à des noms. À partir des objets, il faut abstraire pour découvrir les propriétés, attributs et méthodes. Une réflexion sur le cycle de vie de l'objet et sur ses collaborations avec les autres objets permet de préciser les méthodes, et par là les attributs manipulés par ces méthodes. UML fournit des outils pour représenter cycle de vie et collaboration : ce sont les diagrammes d'état et de collaboration, dont l'étude dépasse le cadre de cet ouvrage.
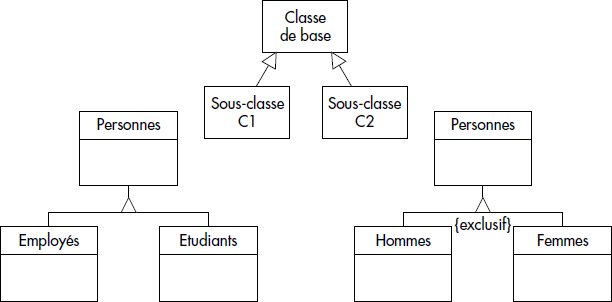
La découverte des classes conduit à découvrir les liens de généralisation et de spécialisation entre classes. Dans une description en langage naturel, les objets sont alors reliés par le verbe « être » (relation is a). UML permet la représentation de l'héritage comme indiqué figure XVII.7. S'il est possible de grouper les deux flèches en une seule, cela n'a pas de signification particulière. Si les deux sous-classes sont disjointes, une contrainte {Exclusive} peut être explicitement notée. De même, il est possible de préciser {Inclusive} si tout objet se retrouve dans toutes les sous-classes. Un nom discriminant peut être ajouté sur l'arc de spécialisation, pour distinguer différentes spécialisations d'une classe.
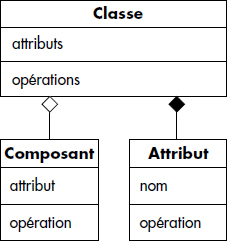
L'agrégation est utilisée pour représenter les situations où une classe est composée d'un ou plusieurs composants. UML permet de distinguer l'agrégation indépendante de l'agrégation composite. La première est une association particulière qui relie un objet à un ou plusieurs objets composants ; les deux classes sont deux classes autonomes. La seconde permet de représenter des objets composites résultant de l'agrégation de valeurs. Elle se distingue de la première par un losange plein. Les diagrammes représentant ces deux types d'associations sont symbolisés figure XVII.8.
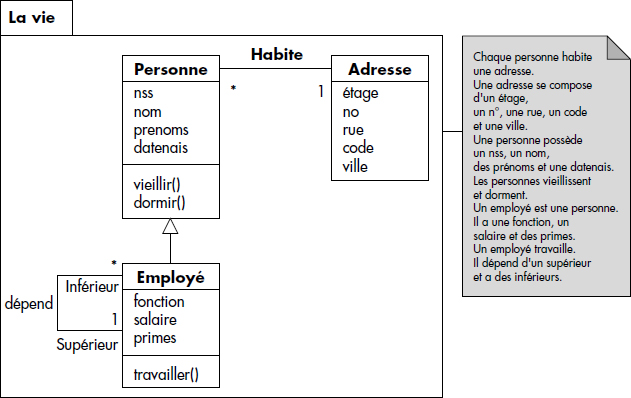
Les figures XVII.9 et XVII.10 illustrent les constructions introduites par deux études de cas conduisant à l'élaboration de schémas externes ou vues, ou encore paquetages (un paquetage UML est un ensemble de composants objets qui peut comporter beaucoup d'autres éléments). Chaque paquetage est représenté par un rectangle étiqueté contenant ses composants. UML permet d'ajouter des notes à tous les niveaux. Pour les paquetages, nous définissons dans la note associée la situation correspondante en français.
XXII-2-3. INTÉGRATION DE SCHÉMAS EXTERNES▲
Les schémas externes ou vues ou encore paquetages permettent donc de représenter des sous-ensembles du schéma conceptuel de la base de données. Construire le schéma externe nécessite d'intégrer ces différentes parties, ce qui n'est pas une tâche simple. Les difficultés proviennent des recouvrements et des liens sémantiques entre parties. De nombreux travaux ont été effectués pour intégrer des schémas objet, non seulement dans le domaine de la conception [Batini86, Navathe84], mais aussi dans celui des bases de données objet fédérées [WonKim95].
Les conflits peuvent concerner les noms des classes et associations (synonymes et homonymes), les structures (attributs manquants, associations regroupées), les définitions d'attributs (conflits, inclusion), les contraintes (cardinalités), etc. La figure XVII.11 propose une liste plus ou moins exhaustive des conflits possibles [WonKim95].
Classe ↔ Classe
Noms différents pour des classes équivalentes
Noms identiques pour des classes différentes
Inclusion de l'une dans l'autre
Intersection non vide
Contraintes entre instances
Attribut ↔ Attribut
Noms différents pour des attributs équivalents
Noms identiques pour des attributs différents
Types différents
Compositions différentes
Classe ↔ Attribut
Significations identiques
Compositions similaires
Association ↔ Association
Noms différents pour des associations équivalentes
Noms identiques pour des associations différentes
Cardinalités différentes
Données différentes
Compositions de plusieurs autres
Agrégation ↔ Agrégation
Agrégation composite versus non-composite
Cardinalités différentes
Association ↔ Attribut
Association versus référence
Cardinalités incompatiblesLe premier problème est d'isoler les conflits. Cela nécessite le passage par un dictionnaire unique des noms, voire par une ontologie. Une ontologie est une définition complète des concepts, avec leurs relations sémantiques. L'utilisation d'une ontologie spécifique au domaine permet de ramener les concepts à un référentiel unique et de mesurer la distance et le recouvrement entre eux [Métais97]. On peut ainsi isoler les conflits potentiels.
Pour chaque cas, des solutions doivent être envisagées, telles que :
- Changement de dénomination de classes, d'associations ou d'attributs.
- Ajout d'attributs ou remplacement par des opérations.
- Définition de classes plus générales ou plus spécifiques.
- Transformation d'agrégation en objets composites et vice versa.
- Redéfinition de types plus généraux.
- Transformation de représentation.
- Conversion et changement d'unités.
Certains conflits ne sont solubles que manuellement. Un outil graphique d'aide à l'intégration peut être avantageusement utilisé.
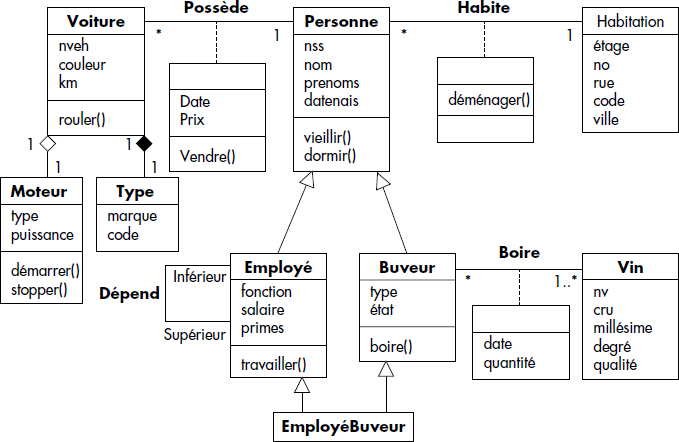
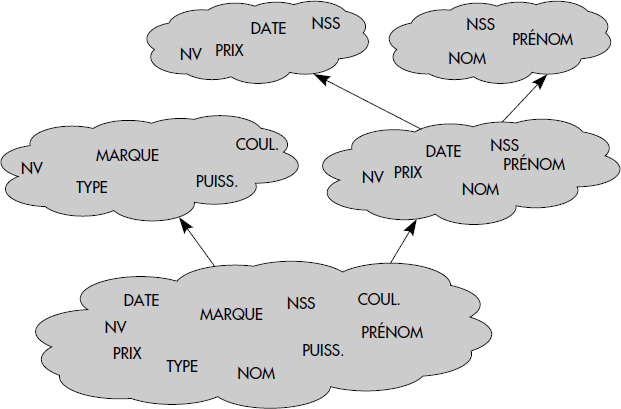
En résumé, après des transformations de schémas automatiques ou manuelles, les schémas externes peuvent être intégrés afin d'obtenir un schéma global cohérent avec un minimum de redondance. À titre d'illustration, la figure XVII.12 (ci-avant) propose un schéma intégré résultant de l'intégration des vues « La vie » et « La voiture » avec nos éternels buveurs (« La fête »). Vous pouvez repérer les transformations effectuées, qui sont assez réduites.
XXII-3. CONCEPTION DU SCHÉMA LOGIQUE▲
Cette section explique comment obtenir un schéma relationnel ou objet-relationnel à partir d'un schéma objet représenté en UML. Nous proposons deux méthodes, la première pour passer de l'objet (et donc d'entité-association qui en est un cas particulier) au relationnel appelée UML/R, la seconde pour passer de l'objet à l'objet-relationnel, appelée UML/OR ou UML/RO selon que la dominance est donnée à l'objet ou au relationnel.
XXII-3-1. PASSAGE AU RELATIONNEL : LA MÉTHODE UML/R▲
XXII-3-1-1. Cas des entités et associations▲
Examinons tout d'abord comment traduire des entités et associations simples. Le modèle relationnel se prête bien à la représentation des entités et des associations. Les règles sont les suivantes :
- R1. Une entité est représentée par une relation (table) de même nom ayant pour attributs la liste des attributs de l'entité.
- R2. Une association est représentée par une relation de même nom ayant pour attributs la liste des clés des entités participantes et les attributs propres de l'association.
Pour appliquer la règle 2, chaque table résultant de la règle 1 doit posséder une clé primaire, c'est-à-dire un groupe d'attributs (1, 2 ou 3 au plus sont conseillés) qui détermine à tout instant un tuple unique dans la table. S'il n'en est pas ainsi, il faut ajouter une clé qui est un numéro de tuple (une séquence attribuée par le système en SQL2). Les tables résultant des associations ont pour clés la liste des clés des entités participantes avec éventuellement, en cas d'association multivaluée, une ou plusieurs données propres de l'association.
Par exemple, les entités PERSONNE et VOITURE de la figure XVII.4 seront respectivement représentées par les relations :
PERSONNE (NSS, NOM, PRENOM, DATENAIS)
VOITURE (NV, MARQUE, TYPE, PUISSANCE, COULEUR)Les clés sont respectivement NSS et NV. En conséquence, l'association POSSÈDE sera représentée par la relation :
POSSEDE (NSS, NV, DATE, PRIX)Les transformations proposées donnent autant de relations que d'entités et d'associations. Il est possible de regrouper certaines relations et associations dans les cas particuliers où un tuple d'une table référence un et un seul tuple de l'association. Une telle association est dite bijective avec l'entité : en effet, tout tuple de la table correspond à un tuple de l'association et réciproquement. La règle est la suivante :
- R3. Une association bijective, c'est-à-dire de cardinalités minimale et maximale 1, peut être regroupée en une seule table avec la relation attachée par jointure sur la clé de l'entité.
Cette règle est illustrée figure XVII.13. Dans le cas où l'association est 1..1 des deux côtés, la règle peut être appliquée à droite ou à gauche, et si les deux entités ne sont reliées à aucune autre association, elles peuvent même être regroupées en une seule table.
Pour implémenter un modèle objet, il n'est pas nécessaire d'avoir une BD objet. Au-delà des entités et associations, tous les concepts d'un modèle objet peuvent être implémentés avec un SGBD relationnel. Alors que les tables mémorisent l'état des objets, les méthodes apparaissent comme des attributs calculés. Elles seront généralement implémentées sous forme de procédures stockées. Nous allons maintenant examiner le passage d'un modèle UML au relationnel, sachant que ce que nous avons dit pour les associations reste vrai dans le contexte objet. La plupart des règles décrites ci-dessous ont été implémentées dans le système expert SECSI d'aide à la conception de bases de données [Bouzeghoub85].
XXII-3-1-2. Cas des généralisations avec héritage▲
Les systèmes relationnels ne connaissent pas les concepts de généralisation et d'héritage. Il faut donc réaliser statiquement ce dernier lors de la transformation du schéma. Pour les données, cela ne pose pas trop de problèmes et plusieurs solutions sont possibles, consistant toutes à aplatir les hiérarchies de spécialisation. Pour les méthodes, le polymorphisme doit être réalisé dans le corps de la méthode par des tests (CASE). Nous examinons ici la transformation des données, comme il se doit pour une base de données.
La solution la plus naturelle pour traduire une hiérarchie de généralisations de classes C1, C2, …, Cn vers une classe C est d'appliquer la règle suivante, en plus de la règle R1 qui conduit à traduire chaque classe (ou entité) comme une table avec une clé primaire, la règle suivante :
- R4.a Une spécialisation d'une classe C en plusieurs classes C1, C2, …, Cn est traduite par répétition de la clé de la table représentant C au niveau de chacune des tables représentant C1, C2, …, Cn.
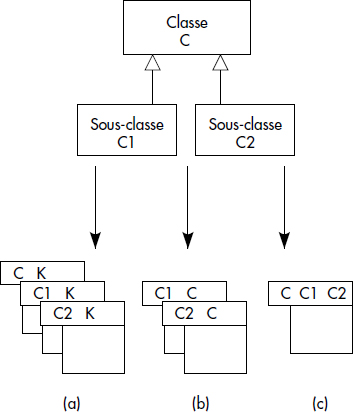
Cette solution conduit à une table par classe (voir figure XVII.14(a)). Lorsqu'on souhaite retrouver un attribut hérité dans une classe dérivée, il faut effectuer une jointure avec la table représentant la classe de base. L'héritage doit donc être accompli par les programmes d'application. La définition d'une vue jointure des tables dérivées et de la table de base (par exemple C|X|C1) permet d'automatiser l'héritage.
D'autres solutions sont possibles pour traduire des spécialisations, comme le montre la figure XVII.14(b) et (c). La solution (b) consiste à faire une table par classe feuille de la hiérarchie en appliquant la règle suivante :
- R4.b Une spécialisation d'une classe C en plusieurs classes C1, C2, …, Cn est traduite par répétition des attributs représentant C au niveau de chacune des tables représentant C1, C2, …, Cn et par transformation de C en une vue dérivée de C1, C2, …, Cn par union des projections sur les attributs de C.
Le problème avec cette solution survient lorsque les classes C1, C2…, Cn ne sont pas exclusives et contiennent des objets communs. Les attributs de C sont alors répétés dans chacune des tables C1, C2, …, Cn, ce qui pose des problèmes de cohérence. Cette règle sera donc seulement appliquée dans le cas d'héritage exclusif. Par exemple, il est intéressant de représenter la hiérarchie d'héritage FEMMES, HOMMES → PERSONNES de la figure XVII.7 par les tables FEMMES et HOMMES, la table PERSONNES pouvant être dérivée par une vue. Au contraire, la même technique utilisée pour la hiérarchie d'héritage EMPLOYES, ETUDIANTS → PERSONNES conduirait à dupliquer les employés étudiants. On préférera alors appliquer la règle R4.a conduisant à trois tables EMPLOYES, ETUDIANTS et PERSONNES, chacune ayant pour clé le numéro de sécurité sociale de la personne.
Une autre solution encore possible consiste à implémenter une seule table comme illustré figure XVII.14(c) :
- R4.c Une spécialisation d'une classe C en plusieurs classes C1, C2, …, Cn est traduite par une table unique comportant la traduction de la classe C complétée avec les attributs de C1, C2, …, Cn, les tables correspondant à C1, C2, …, Cn étant des vues dérivées de C par projection sur les attributs pertinents.
Le problème avec cette solution survient lorsqu'un objet de la classe C n'a pas de spécialisation dans une sous-classe Ci : dans ce cas, tous les attributs de la classe Ci apparaissent comme des valeurs nulles ! Par exemple, pour la hiérarchie FEMMES, HOMMES → PERSONNES, les attributs spécifiques aux femmes seront nuls pour chaque homme dans la table PERSONNES générale (par exemple, le nom de jeune fille). Pour la hiérarchie EMPLOYES, ETUDIANTS → PERSONNES, tout employé non étudiant aura les attributs d'étudiants nuls et tout étudiant non employé aura les attributs spécifiques aux étudiants nuls. Cette solution n'est donc bonne que dans le cas d'héritage complet, où chaque objet de la classe de base est membre de la sous-classe.
En résumé, les différents cas sont illustrés figure XVII.14. Bien sûr, ils peuvent être mixés et il faut réfléchir pour chaque sous-classe. Certaines peuvent par exemple être regroupées avec la classe de base, d'autres implémentées de manière autonome.
XXII-3-1-3. Cas des agrégations et collections▲
Comme nous l'avons vu ci-dessus, UML propose deux cas d'agrégations : les agrégations indépendantes et les agrégations composites.
L'agrégation indépendante n'est rien de plus qu'un cas particulier d'association : elle sera donc traduite en appliquant les règles des associations. Un problème peut être que les agrégations n'ont pas de nom en général : il faut en générer un, par exemple par concaténation des noms des entités participantes. On ajoutera un nom de rôle si plusieurs agrégations indépendantes relient deux classes.
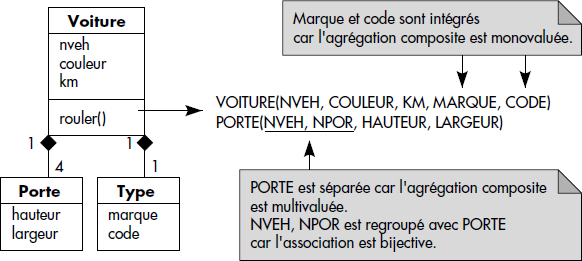
L'agrégation composite correspond à un groupe d'attributs (et méthodes) imbriqués dans l'objet composite. Dans le cas de bijection (cardinalité 1..1), tous les attributs de la classe cible (le composant) sont simplement ajoutés à la table représentant la classe source (le composé). La classe cible est représentée par une vue. La règle est la suivante :
- R5. Une classe dépendant d'une autre par une agrégation composite monovaluée est représentée par des attributs ajoutés à la table représentant l'objet composite et si nécessaire transformée en une vue, sinon omise.
Cette règle est appliquée figure XVII.15. Au-delà, le relationnel pur ne permet pas de traduire les agrégations composites multivaluées par une seule table. On procède alors comme avec une agrégation indépendante et plus généralement une association. Des contraintes d'intégrité additionnelles peuvent être ajoutées, comme nous le verrons ci-dessous.
Les attributs multivalués peuvent être intégrés directement dans une classe par le biais de collections SET<X>, LIST<X>, BAG<X>, etc. Une bonne modélisation UML traduit de tels attributs en agrégations composites. Cependant, il est permis d'utiliser des templates ; alors le problème de la traduction en relationnel se pose.
Deux cas sont à considérer pour traduire en relationnel. Si le nombre maximal N de valeurs est connu et faible (< 5 par exemple), il est possible de déclarer N colonnes, de nom A1, A2, etc., où A est le nom de l'attribut. Cette solution manque cependant de flexibilité et conduit à des valeurs nulles dès qu'il y a moins de N valeurs. Une solution plus générale consiste à isoler la clé K de la table résultant de la classe ayant un attribut collection, et à créer une table répertoriant les valeurs de la collection associée à la clé. La table a donc pour schéma AS (K, A) et donne les valeurs de A pour chaque valeur de K. Par exemple, si une collection a trois valeurs v1, v2, v3 pour la clé 100, (100-v1), (100-v2) et (100-v3) seront trois tuples de la table AS. Les collections seront reconstituées par des jointures lors des interrogations. Cette solution est connue sous le nom de passage en première forme normale et nous y reviendrons ci-dessous.
XXII-3-1-4. Génération de contraintes d'intégrité▲
Au-delà des tables, le passage d'un modèle objet exprimé en UML au relationnel permet de générer des contraintes d'intégrité référentielles. Les associations sont particulièrement utiles pour cela. Voici deux règles applicables :
- R6. Toute association E1→R→E2 représentée par une table R non intégrée à E1 ou E2 donne naissance à deux contraintes référentielles : R.K(E1) référence E1 et R.K(E2) référence E2, K(Ei) désignant la clé de Ei.
- R7. Toute association E1→R→E2 de cardinalité minimale 1 sur E2 représentée par une table non intégrée à E1 donne naissance à une contrainte référentielle additionnelle : E1.K(E1) référence R.K(E1).
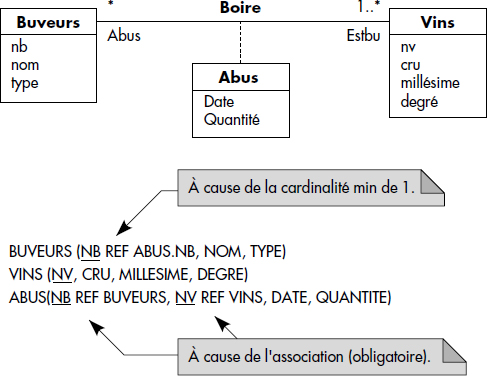
Ces règles sont illustrées figure XVII.16 sur l'association Boire entre Buveurs et Vins. La contrainte de Buveurs vers Abus résulte du fait que la cardinalité minimale de 1 signifie que pour un objet quelconque, il existe au moins une instance d'association (règle 7). Les contraintes référentielles de la table associative Abus vers Buveurs et Vins proviennent du fait que l'association implique l'existence des objets associés (règle 6). En théorie, les associations sont donc très contraignantes pour le modèle relationnel sous-jacent. On omet parfois les contraintes résultant de la règle 6, ce qui signifie qu'on tolère des associations entre objets non existants.
XXII-3-2. PASSAGE À L'OBJET-RELATIONNEL : UML/RO OU UML/OR?▲
Les SGBD deviennent objet-relationnels avec SQL3, comme nous l'avons montré au chapitre XIII. Passer d'un modèle UML à un modèle objet-relationnel est à la fois plus simple et plus compliqué. C'est plus simple en théorie, car l'objet-relationnel supporte directement les associations, l'héritage et les collections. C'est plus complexe, car il y a maintenant des types et des tables, et tous les types possibles en objet ne sont pas possibles en objet-relationnel. De plus, la représentation relationnelle reste possible. Alors que faire ? Deux approches au moins sont possibles : l'une étendant simplement l'approche relationnelle avec des types utilisateurs, l'autre beaucoup plus proche de l'objet.
L'approche relationnelle étendue (notée UML/RO, le R venant en premier) consiste à faire une première passe sur le schéma objet afin d'isoler les types intéressants. Ceux-ci peuvent être des groupes d'attributs qui apparaissent de manière répétitive dans différentes classes ou des groupes d'attributs supports de méthodes. On s'attachera à chercher des types significatifs pour l'entreprise ou le métier. Les types resteront réduits à quelques attributs, et couvriront rarement une classe entière. L'objectif est de rester dans une démarche relationnelle, simplement en ajoutant quelques types fondamentaux aux types de base SQL entier, réel, caractères et date. Une fois isolés, ces types seront définis comme tels, des attributs typés remplaceront les groupes isolés, et la démarche UML/R précédente sera appliquée pour générer les tables. Cette méthode présente l'avantage de continuité et laisse possible l'application des techniques de normalisation que nous allons étudier ci-dessous, en considérant les instances des types utilisés comme atomiques.
La démarche objet (notée UML/OR, le O venant en premier) au contraire va tout transformer en type et voir les tables comme des extensions de type. Une technique peut consister à procéder systématiquement comme suit :
- Pour chaque classe, générer le type SQL3 correspondant par la commande CREATE TYPE. Utiliser l'héritage de type pour traduire les spécialisations et l'agrégation de type pour les agrégations composites.
-
Si une classe n'est pas cible d'une agrégation composite ou d'une généralisation, alors l'implémenter comme une table d'objets du type associé. Cela conduit :
- À implémenter toutes les classes feuille des hiérarchies d'héritage en incluant les attributs hérités, comme dans le cas (b) de la figure XVII.14. D'autres choix sont possibles, comme cela a déjà été signalé ci-dessus.
- À respecter les agrégations composites en ce sens que les instances de la classe cible figureront dans la table associée à l'autre classe.
- Implémenter toutes les associations par des attributs références mono ou multivalués (en respectant les cardinalités maximales de l'association) d'une table vers une autre, éventuellement dans les deux sens. L'utilisation de références dans les deux sens permet les parcours de chemins dans les deux sens. C'est utile si les requêtes le nécessitent.
En fait, aujourd'hui, bien peu de SGBD objet-relationnels supporteront une telle démarche pour une grosse base (quelques centaines de classes). Elle conduit en effet à gérer beaucoup de types et beaucoup de références. De plus, le schéma résultat ne peut être normalisé simplement et peut présenter des difficultés d'évolutions, les types étant souvent liés par héritage ou par agrégation. Nous conseillerons donc plutôt l'approche UML/RO plus compatible avec la théorie héritée du relationnel que nous étudions ci-dessous.
XXII-4. AFFINEMENT DU SCHÉMA LOGIQUE▲
Cette section justifie la nécessité d'une étape d'affinement des schémas relationnels et introduit les approches possibles pour réduire les problèmes soulevés par une mauvaise perception du réel.
XXII-4-1. ANOMALIES DE MISE À JOUR▲
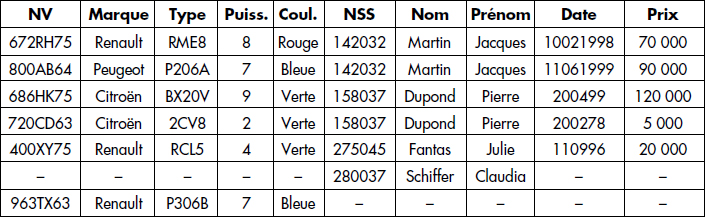
Une mauvaise conception des entités et associations représentant le monde réel modélisé conduit à des relations problématiques. Imaginons par exemple que l'on isole une entité unique PROPRIETAIRE contenant tous les attributs des trois relations PERSONNE, VOITURE et POSSEDE. Ainsi, nous pourrions représenter toutes les informations modélisées par une seule table. La figure XVII.17 représente une extension possible de cette table.
La relation représentée figure XVII.17 souffre de plusieurs types d'anomalies [Codd72, Fagin81] :
- Tout d'abord, des données sont redondantes : par exemple, MARTIN Jacques et DUPOND Pierre apparaissent deux fois ; plus généralement, une personne apparaît autant de fois qu'elle possède de voitures.
- Ces redondances conduisent à des risques d'incohérences lors des mises à jour. Par exemple, si l'on s'aperçoit que le prénom de DUPOND n'est pas Pierre mais Jean, il faudra veiller à mettre à jour les deux tuples contenant DUPOND, sous peine de voir apparaître un DUPOND Pierre et un DUPOND Jean.
- Il est nécessaire d'autoriser la présence de valeurs nulles dans une telle relation afin de pouvoir conserver dans la base des voitures sans propriétaire ou des personnes ne possédant pas de voitures.
En résumé, une relation qui ne représente pas de « vraies » entités ou associations semble donc souffrir de la présence de données redondantes et d'incohérences potentielles, et nécessite le codage de valeurs nulles. En réalité, un fait élémentaire est enregistré plusieurs fois dans une relation résultant de la jointure de plusieurs entités et associations. De plus, les faits élémentaires sont artificiellement associés si bien qu'ils ne peuvent être insérés indépendamment. Il y a tout intérêt à éliminer ces anomalies d'insertion, de mise à jour et de suppression afin de faciliter la manipulation des relations.
XXII-4-2. PERTE D'INFORMATIONS▲
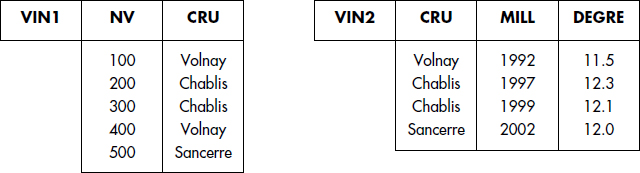
Une analyse simpliste des exemples précédents pourrait laisser croire que les relations problématiques sont celles ayant trop d'attributs. Une méthode simple pour éviter les problèmes pourrait être de n'utiliser que des relations binaires à deux colonnes. Malheureusement, des faits élémentaires associent plus de deux valeurs d'attributs. Cela se traduit par le fait qu'un découpage par projections d'une table peut conduire à ne plus être capable de retrouver les informations du monde réel représentées par jointure : on dit qu'il y a perte d'informations. Un exemple est représenté figure XVII.18.
L'entité VIN a été représentée par deux tables VIN1 et VIN2. En interrogeant par des jointures et projections, et plus généralement en SQL, il est impossible de retrouver précisément le degré d'un vin ou la qualité d'un cru millésimé. Il y a perte de sémantique, car la jointure naturelle des deux tables VIN1 et VIN2 sur l'attribut commun CRU ne permet pas de retrouver les vins de départ, avec un degré unique (par exemple pour les Chablis).
XXII-4-3. L'APPROCHE PAR DÉCOMPOSITION▲
L'approche par décomposition à la conception des schémas relationnels tend à partir d'une relation composée de tous les attributs, appelée la relation universelle, et à la décomposer en sous-relations ne souffrant pas des anomalies précédemment signalées.
Notion XVII.2 : Relation universelle (Universal relation)
Table unique dont le schéma est composé par union de tous les attributs des tables constituant la base.
La définition de cette relation universelle suppose préalablement une nomination des attributs telle que deux attributs représentant le même concept aient le même nom et deux attributs représentant des concepts distincts aient des noms différents.
Le processus de décomposition est un processus de raffinements successifs qui doit aboutir (du moins on l'espère) à isoler des entités et des associations élémentaires, ou si l'on préfère canoniques, du monde réel. Il doit être réalisé à partir d'une bonne compréhension des propriétés sémantiques des données. Cette approche est illustrée par la figure XVII.19. La compréhension de la théorie de la décomposition des relations nécessite la bonne connaissance des deux opérations élémentaires de manipulation de relations que sont la projection et la jointure. En effet, nous allons décomposer par projection et recomposer par jointure.
Il est maintenant possible d'introduire plus précisément la notion de décomposition [Ullman88].
Notion XVII.3 : Décomposition (Decomposition)
Remplacement d'une relation R (A1, A2…, An) par une collection de relations R1, R2, …, Rn obtenue par des projections de R sur des sous-ensembles d'attributs dont l'union contient tous les attributs de R.
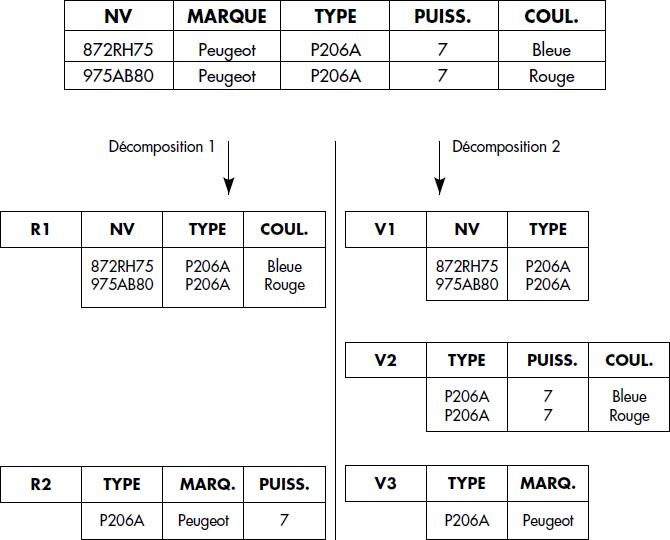
Par suite, lors d'une décomposition, le schéma de relation R (A1, A2… An) est remplacé par une collection de schémas dont l'union des attributs est (A1, A2… An). La jointure naturelle R1 |X| R2 |X| Rn constitue donc une relation de même schéma que R, mais dont les tuples ne sont pas forcément les mêmes que ceux de R. À titre d'illustration, la figure XVII.20 propose deux décompositions possibles pour la relation VOITURE.
Si l'on admet qu'à un type de véhicule sont associées une seule marque et une seule puissance (ce qui est vrai pour les tuples figurant sur des cartes grises), la décomposition 1 est plus plaisante que l'autre : elle permet de retrouver toutes les informations par jointure, alors que la décomposition 2 ne permet pas de retrouver la couleur d'un véhicule ; la jointure V1 ![]() V2
V2 ![]() V3 est différente de la relation initiale VOITURE. D'où la notion de décomposition sans perte (d'information).
V3 est différente de la relation initiale VOITURE. D'où la notion de décomposition sans perte (d'information).
Notion XVII.4 : Décomposition sans perte (Lossless join decomposition)
Décomposition d'une relation R en R1, R2, …, Rn telle que pour toute extension de R, on ait : R = R1 ![]() R2
R2 ![]() … Rn.
… Rn.
Le problème de la conception des bases de données relationnelles peut donc être perçu comme celui de décomposer la relation universelle composée de tous les attributs en sous-relations ne souffrant pas des anomalies vues ci-dessus, de sorte à obtenir une décomposition sans perte. La décomposition a été introduite par Codd [Codd71] et a donné lieu a de nombreux travaux à la fin des années 70 pour « casser en morceaux les relations ». Nous allons ci-dessous étudier les principales méthodes proposées pour effectuer une telle décomposition, qui devraient permettre de déterminer des entités et associations canoniques du monde réel, donc en fait de générer un schéma conceptuel. Ces méthodes ont été développées dans [Rissanen73] puis généralisées dans [Fagin77] et [Zaniolo81].
En pratique, on ne part généralement pas de la relation universelle, mais plutôt du schéma logique obtenu par la modélisation entité-association ou objet, puis par application des règles de passage au relationnel étudiées ci-dessus. Ce processus conduit de fait à une première décomposition intuitive. Si elle est trop fine, il se peut que des informations soient perdues.
XXII-4-4. L'APPROCHE PAR SYNTHÈSE▲
L'approche par synthèse [Bernstein76] procède par recomposition des relations à partir d'un ensemble d'attributs indépendants. Fondée sur les propriétés sémantiques des attributs et des liens entre eux, les relations sont composées progressivement de façon à ne pas souffrir des anomalies précédemment mentionnées (voir figure XVII.21 page suivante). Les approches par synthèse s'appuient souvent sur un graphe représentant les liens interattributs. Nous verrons un algorithme de synthèse plus loin.
XXII-5. DÉPENDANCES FONCTIONNELLES▲
Dans cette section, nous étudions les liens sémantiques entre attributs, particulièrement les liens fonctionnels.
XXII-5-1. QU'EST-CE QU'UNE DÉPENDANCE FONCTIONNELLE ?▲
La notion de dépendance fonctionnelle fut introduite dès le début du relationnel par CODD afin de caractériser des relations pouvant être décomposées sans perte d'informations.
Notion XVII.5 : Dépendance fonctionnelle (Functional dependency)
Soit R (A1, A2… An) un schéma de relation, et X et Y des sous-ensembles de {A1, A2, …, An}. On dit que X → Y (X détermine Y, ou Y dépend fonctionnellement de X) si pour toute extension r de R, pour tout tuple t1 et t2 de r, on a : ????x (t1) = ????x (t2) ⇒ ????x (t1) = ????Y (t2)
Plus simplement, un attribut (ou groupe d'attributs) Y dépend fonctionnellement d'un attribut (ou groupe d'attributs) X, si, étant donné une valeur de X, il lui correspond une valeur unique de Y (quel que soit l'instant considéré).
À titre d'exemple, dans la relation VOITURE, les dépendances fonctionnelles suivantes existent :
NV → COULEUR
TYPE → MARQUE
TYPE → PUISSANCE
(TYPE, MARQUE) → PUISSANCEPar contre, les dépendances fonctionnelles suivantes sont inexistantes :
PUISSANCE → TYPE
TYPE → COULEURIl est essentiel de bien remarquer qu'une dépendance fonctionnelle (en abrégé, DF) est une assertion sur toutes les valeurs possibles et non pas sur les valeurs actuelles : elle caractérise une intention et non pas une extension d'une relation. Autrement dit, il est impossible de déduire les DF d'une réalisation particulière d'une relation. La seule manière de déterminer une DF est de regarder soigneusement ce que signifient les attributs, car ce sont des assertions sur le monde réel qui lient les valeurs possibles des attributs entre elles. Les DF devraient ainsi être déclarées par l'administrateur d'entreprise au niveau du schéma conceptuel et un bon SGBD devrait les faire respecter.
XXII-5-2. PROPRIÉTÉS DES DÉPENDANCES FONCTIONNELLES▲
Les DF obéissent à plusieurs règles d'inférences triviales. Les trois règles suivantes composent les axiomes des dépendances fonctionnelles et sont connues dans la littérature sous le nom d'axiomes d'Armstrong [Armstrong74] :
- Réflexivité : Y ⊆ X ⇒ X → Y ; tout ensemble d'attributs détermine lui-même ou une partie de lui-même.
- Augmentation : X → Y ⇒ XZ → YZ ; si X détermine Y, les deux ensembles d'attributs peuvent être enrichis par un même troisième.
- Transitivité : X → Y et Y → Z ⇒ X → Z ; cette règle est moins triviale et provient du fait que le composé de deux fonctions dont l'image de l'une est le domaine de l'autre est une fonction. Par exemple, des dépendances NV → TYPE et TYPE → PUISSANCE, on déduit NV → PUISSANCE.
Plusieurs autres règles se déduisent de ces axiomes de base :
- Union : X → Y et X → Z ⇒ X → YZ.
- Pseudotransitivité : X → Y et WY → Z ⇒ WX → Z.
- Décomposition : X → Y et Z ⊆ Y ⇒ X → Z.
À partir de ces règles, il est possible d'introduire la notion de dépendance fonctionnelle élémentaire [Zaniolo81].
Notion XVII.6 : Dépendance fonctionnelle élémentaire (Elementary functional dependancy)
Dépendance fonctionnelle de la forme X → A, où A est un attribut unique n'appartenant pas à X (A ∉ X) et où il n'existe pas X' ⊂ X tel que X' → A.
La seule règle d'inférence qui s'applique aux dépendances fonctionnelles élémentaires est la transitivité.
XXII-5-3. GRAPHE DES DÉPENDANCES FONCTIONNELLES▲
Soit un ensemble F de dépendances fonctionnelles élémentaires. Si tous les attributs gauches sont uniques, il est possible de visualiser cet ensemble de DF par un graphe appelé graphe des dépendances fonctionnelles. À titre d'exemple, nous considérons les dépendances fonctionnelles entre les attributs de la relation VOITURE figure XVII.22.
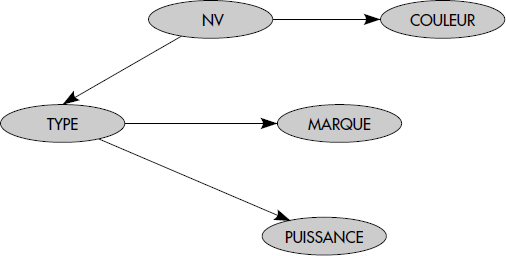
Il n'est pas toujours possible de représenter les DF d'une relation par un graphe simple : si une partie gauche d'une DF comporte plus d'un attribut, il faut introduire des arcs représentant une association de plusieurs sommets vers un sommet. Nous pouvons alors utiliser la notation des réseaux de Pétri pour représenter les dépendances (voir figure XVII.23).
En effet, la relation :
REDUCTION (CRU, TYPE, CLIENT, REMISE)dans laquelle :
- un cru possède un type associé et un seul,
- les réductions sont effectuées selon le type et le client,
comporte une dépendance à partie gauche multiple :
TYPE, CLIENT → REMISEDe même, la relation CODE POSTAL (CODE, VILLE, RUE) comporte les DF :
(VILLE, RUE) → CODE
CODE → VILLELa dépendance (VILLE,RUE) → CODE nécessite un réseau.
XXII-5-4. FERMETURE TRANSITIVE ET COUVERTURE MINIMALE▲
À partir d'un ensemble de DF élémentaires, on peut composer par transitivité d'autres DF élémentaires. On aboutit ainsi à la notion de fermeture transitive d'un ensemble F de DF élémentaires : c'est l'ensemble des DF élémentaires considérées enrichi de toutes les DF élémentaires déduites par transitivité.
Par exemple, à partir de l'ensemble de DF :
F = { NV → TYPE ; TYPE → MARQUE ; TYPE → PUISSANCE ;
NV → COULEUR}on déduit la fermeture transitive :
F+ = F ∪ {NV → MARQUE ; NV → PUISSANCE}Le graphe correspondant à F+ est représenté figure XVII.24.
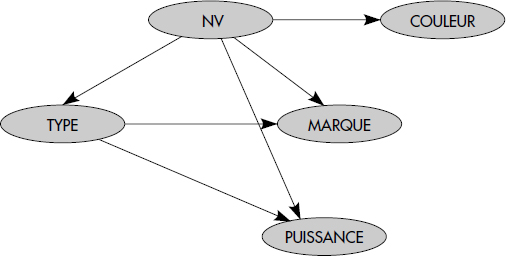
À partir de la notion de fermeture transitive, il est possible de définir l'équivalence de deux ensembles de DF élémentaires : deux ensembles sont équivalents s'ils ont la même fermeture transitive. Par suite, il est intéressant de déterminer un sous-ensemble minimal de DF permettant de générer toutes les autres. C'est la couverture minimale d'un ensemble de DF.
Notion XVII.7 : Couverture minimale (Minimal cover)
Ensemble F de DF élémentaires associé à un ensemble d'attributs vérifiant les propriétés suivantes :
- Aucune dépendance dans F n'est redondante, ce qui signifie que pour toute DF f de F, F - f n'est pas équivalent à F.
- Toute DF élémentaire des attributs est dans la fermeture transitive de F (notée F+).
Il a été montré [Delobel73] que tout ensemble de DF a une couverture minimale qui n'est en général pas unique. Par exemple :
F = {NV → TYPE ; TYPE → MARQUE ; TYPE → PUISSANCE ;
NV → COULEURest une couverture minimale pour l'ensemble des DF de VOITURE. La couverture minimale va constituer un élément essentiel pour composer des relations sans perte d'informations directement à partir des attributs.
XXII-5-5. RETOUR SUR LA NOTION DE CLÉ DE RELATION▲
La notion de clé de relation est un concept de base du modèle relationnel. Bien que la notion intuitive de clé soit bien connue, il est possible d'en donner une définition plus formelle à partir de celle de dépendance fonctionnelle, comme suit.
Notion XVII.8 : Clé de relation (Relation key)
Sous-ensemble X des attributs d'une relation R (A1, A2…, A2) tel que :
- X → A1 A2 … An.
- Il n'existe pas de sous-ensemble Y ∈ X tel que Y → A1 A2 … An.
En clair, une clé est un ensemble minimal d'attributs qui détermine tous les autres. Un ensemble d'attributs qui inclut une clé est appelé superclé. Par exemple, NV est une clé de la relation VOITURE, alors que (NV, TYPE) n'est pas une clé, mais une superclé. Il peut y avoir plusieurs clés pour une même relation : on en choisit en général une comme clé primaire. On parle parfois de clé candidate pour désigner une clé quelconque.
XXII-6. LES TROIS PREMIÈRES FORMES NORMALES▲
Les trois premières formes normales ont pour objectif de permettre la décomposition de relations sans perdre d'informations, à partir de la notion de dépendance fonctionnelle [Codd72]. L'objectif de cette décomposition est d'aboutir à un schéma conceptuel représentant les entités et les associations canoniques du monde réel.
XXII-6-1. PREMIÈRE FORME NORMALE▲
La première forme normale permet simplement d'obtenir des tables rectangulaires sans attributs multivalués irréguliers.
Notion XVII.9 : Première forme normale (First normal form)
Une relation est en première forme normale si tout attribut contient une valeur atomique.
Cette forme normale est justifiée par la simplicité et l'esthétique. Elle consiste simplement à éviter les domaines composés de plusieurs valeurs. Plusieurs décompositions sont possibles, comme vu ci-dessus. Par exemple, la relation PERSONNE(NOM, PRENOMS) pourra être décomposée en PERSONNE1(NOM, PRENOM1) et PERSONNE2(NOM, PRENOM2) si l'on sait que les personnes n'ont pas plus de deux prénoms. Plus généralement, nous avons montré ci-dessus qu'une relation de clé K avec un attribut multivalué A* pouvait être décomposée en deux relations par élimination de l'attribut multivalué et génération d'une table de schéma (K, A) donnant les valeurs élémentaires de A associées aux valeurs de la clé. La règle de décomposition en première forme normale n'est rien d'autre que l'application systématique de cette transformation. Si la relation n'a pas d'autre attribut que la clé et l'attribut multivalué, elle est simplement désimbriquée comme pour l'exemple de la figure XVII.25.

|
Une telle relation doit être décomposée en répétant les noms pour chaque profession (Opération UNNEST) |
Soulignons que la première forme normale est une question de définition de domaine : chaque valeur d'un domaine est en effet un atome du point de vue du modèle relationnel. Par suite, rien n'empêche de considérer une date ou une figure géométrique comme atomique si les domaines de valeur sont les dates et les figures géométriques. C'est une question de point de vue et de niveau de décomposition.
XXII-6-2. DEUXIÈME FORME NORMALE▲
La deuxième forme normale permet d'assurer l'élimination de certaines redondances en garantissant qu'aucun attribut n'est déterminé seulement par une partie de la clé.
Notion XVII.10 : Deuxième forme normale (Second normal form)
Une relation R est en deuxième forme normale si et seulement si :
- Elle est en première forme.
- Tout attribut n'appartenant pas à une clé ne dépend pas d'une partie d'une clé.
Le schéma typique d'une relation qui n'est pas en 2e forme normale est représenté figure XVII.26. K1 et K2 désignent deux parties de la clé K. Le problème est que K2 à lui seul détermine Y : K2 → Y. Donc Y dépend d'une partie de la clé. Comme nous le verrons plus loin, une telle relation doit être décomposée en R1(K1,K2,X) et R2(K2,Y).
Par exemple, considérons la relation :
FOURNISSEUR (NOM, ADRESSE, ARTICLE, PRIX)La clé est le couple (NOM, ARTICLE). Il existe les DF :
(NOM, ARTICLE) → PRIX et NOM → ADRESSE.Par suite, une partie de la clé (NOM) détermine un attribut n'appartenant pas à la clé. Cette relation n'est donc pas en deuxième forme normale. Elle pourra être décomposée en deux relations :
FOURNISSEUR (NOM, ADRESSE)
PRODUIT (NOM, ARTICLE, PRIX)qui, quant à elles, sont en deuxième forme normale.
|
Une telle relation doit être décomposée en R1(K1,K2,X) et R2(K2,Y) |
XXII-6-3. TROISIÈME FORME NORMALE▲
La troisième forme normale permet d'assurer l'élimination des redondances dues aux dépendances transitives.
Notion XVII.11 : Troisième forme normale (Third normal form)
Une relation R est en troisième forme normale si et seulement si :
- Elle est en deuxième forme.
- Tout attribut n'appartenant pas à une clé ne dépend pas d'un autre attribut non-clé.
Soulignons qu'une partie de clé n'est pas une clé. En conséquence, une relation en 3e forme est automatiquement en 2e : la condition 1 est automatiquement vérifiée, mais figure par souci de clarté. Soulignons aussi que si la relation possède plusieurs clés candidates, la définition doit être vérifiée pour chacune d'elles successivement.
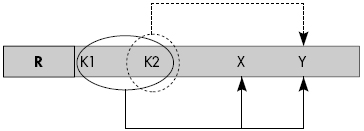
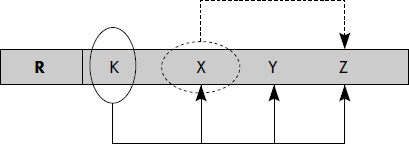
Le schéma typique d'une relation qui n'est pas en 3e forme normale est représenté figure XVII.27. K est la clé de R. Le problème est que X à lui seul détermine Z : X → Z. Donc Z dépend d'un attribut non-clé. Comme nous le verrons plus loin, une telle relation doit être décomposée en R1(K1,X,Y) et R2(X,Z).
|
Une telle relation doit être décomposée en R1(K, X, Y) et R2(X, Z) |
À titre d'illustration, la relation :
VOITURE (NV, MARQUE, TYPE, PUISSANCE, COULEUR)n'est pas en troisième forme normale. En effet, l'attribut non-clé TYPE détermine MARQUE et aussi PUISSANCE. Cette relation peut être décomposée en deux relations :
VOITURE (NV, TYPE, COULEUR)
MODELE (TYPE, MARQUE, PUISSANCE).Si la relation possède une seule clé primaire, il est possible de donner une définition équivalente comme suit. Une relation R est en troisième forme normale si et seulement si :
- elle est en deuxième forme normale ;
- tout attribut n'appartenant pas à la clé ne dépend pas transitivement de la clé.
Par exemple, dans la relation VOITURE, l'attribut MARQUE dépend transitivement de la clé ainsi que l'attribut PUISSANCE :
NV → TYPE → PUISSANCE,
NV → TYPE → MARQUE.XXII-6-4. PROPRIÉTÉS D'UNE DÉCOMPOSITION EN TROISIÈME FORME NORMALE▲
Les dépendances fonctionnelles sont des règles indépendantes du temps que doivent vérifier les valeurs des attributs. Il est nécessaire qu'une décomposition préserve ces règles.
Notion XVII.12 : Décomposition préservant les dépendances fonctionnelles (Dependencies preserving decomposition)
Décomposition {R1, R2… Rn} d'une relation R telle que la fermeture transitive des DF de R est la même que celle de l'union des DF de {R1, R2… Rn}.
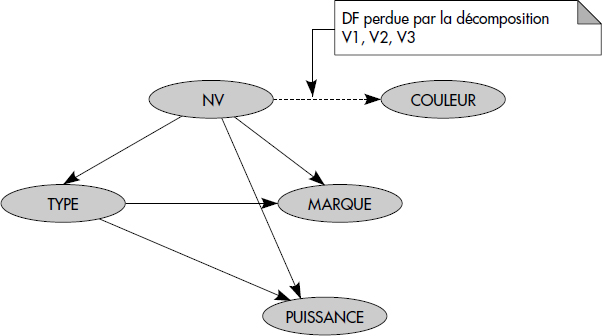
À titre d'exemple, la décomposition de la relation VOITURE(NV, MARQUE, TYPE, PUISSANCE, COULEUR) en R1(NV, TYPE, COULEUR) et R2(TYPE, MARQUE, PUISSANCE) préserve les DF, alors que la décomposition en V1(NV, TYPE), V2(TYPE, PUISSANCE, COULEUR) et V3(TYPE, MARQUE) ne les préserve pas, comme le montre la figure XVII.28.
La troisième forme normale est importante. En effet, toute relation a au moins une décomposition en troisième forme normale telle que :
- La décomposition préserve les DF ;
- La décomposition est sans perte.
Cette décomposition peut ne pas être unique. Nous allons dans la suite étudier un algorithme permettant de générer une telle décomposition.
XXII-6-5. ALGORITHME DE DÉCOMPOSITION EN TROISIÈME FORME NORMALE▲
Pour toute relation, y compris la relation universelle, il existe donc au moins une décomposition en troisième forme normale préservant les DF et sans perte. Le but d'un algorithme de décomposition en 3e forme normale est de convertir un schéma de relation qui n'est pas en 3e FN en un ensemble de schémas en 3e FN. Le principe consiste simplement à appliquer récursivement les règles de décomposition énoncées ci-dessus, afin de décomposer jusqu'à obtenir des relations en 3e FN.
Revenons quelque peu sur ces règles afin de montrer leur validité. Soit donc une relation de schéma R(K1, K2, X, Y) qui n'est pas en 2e FN. La figure XVII.29 donne le graphe de DF associé. Les cercles correspondant aux relations décomposées R1(K1,K2, X) et R2(K2,Y) montrent simplement que l'union des DF de R1 et R2 est bien l'ensemble des DF : cette décomposition préserve les DF. D'un autre côté, par jointure sur K2, on retrouve bien la relation initiale. Donc, la décomposition est sans perte. Les deux relations sont bien en 2e FN. Cette règle de décomposition a donc toutes les bonnes propriétés.
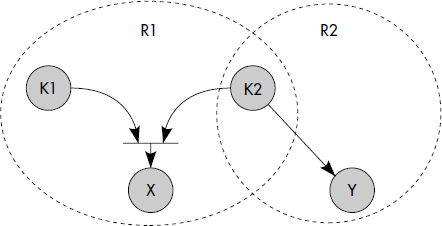
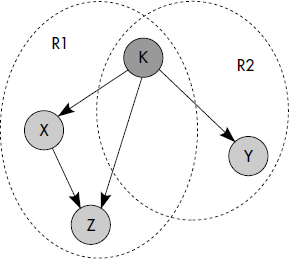
On vérifie de manière similaire les bonnes propriétés de la décomposition en 3e FN, comme illustré figure XVII.30.
XXII-6-6. ALGORITHME DE SYNTHÈSE EN TROISIÈME FORME NORMALE▲
Une décomposition en 3e FN peut être générée par un algorithme de synthèse ayant pour entrées l'ensemble des attributs ainsi que les DF. Le principe d'un tel algorithme [Bernstein76] consiste à construire tout d'abord une couverture minimale F des DF élémentaires. Ensuite, la couverture F doit être partitionnée en groupes Fi tels que les DF dans chaque Fi aient le même ensemble d'attributs à gauche. Chaque groupe produit une relation en 3e FN.
Pour produire un groupe, on recherche le plus grand ensemble X d'attributs qui détermine d'autres attributs A1, A2… An (avec n ≥ 1), et l'on extrait la relation (X1, A1, A2 … An). Une telle relation de clé X est bien en 3e forme normale, car X détermine tous les autres attributs et il ne peut exister de dépendances transitives X → Ai → Aj du fait que l'on est parti d'une couverture minimale (sinon, X → Aj ne serait pas dans cette couverture). Les DF X → A1, X → A2…, X → An sont alors éliminées de la couverture minimale, ainsi que les attributs isolés créés (non source ou cible de DF). L'algorithme est ensuite appliqué itérativement jusqu'à ce qu'il ne reste plus de groupe. S'il reste des attributs isolés, on les sort dans une table qui est bien en 3e FN puisqu'elle n'a pas de DF entre ses attributs. Cet algorithme est schématisé figure XVII.31.
Procédure Synthèse({Ai}, {DF}) { // Normalisation par synthèse
Trouver une couverture minimale F de {DF} ;
Conserver les seules dépendances élémentaires ;
Tant que « il reste des DF » Faire { ProduireGroupe() } ;
Éditer la relation composée des attributs restants ;
}
// Production d'une relation de clé maximale à partir de F
Procédure ProduireGroupe {
X = Rechercher(), // Rechercher le plus grand ensemble
// d'attributs X qui en détermine d'autres ;
A = {Ai | Ai → X} ;
Éditer la relation (X, A) ; // Génération de relation en 3e FN
Pour chaque Ai de A Faire { // Réduction de F
Éliminer toute DF incluse dans (X,Ai) ;
Si Ai est isolé Alors Éliminer Ai de F ;
}
}XXII-6-7. FORME NORMALE DE BOYCE-CODD▲
La 2e forme normale élimine les anomalies créées par des dépendances entre parties de clé et attributs non-clé. La 3e forme normale élimine les anomalies créées par des dépendances entre les attributs non-clés. Quid des dépendances de parties de clés entre elles ou d'attributs non-clé vers une partie de clé ? Eh bien, la 3e FN est insuffisante.
Afin d'éliminer les redondances créées par des dépendances entre parties de clés et celles déjà éliminées par la 3e FN, Boyce et Codd ont introduit la forme normale qui porte leur nom (en abrégé BCNF) [Codd74].
Notion XVII.13 : Forme normale de Boyce-Codd (Boyce-Codd normal form)
Une relation est en BCNF si et seulement si les seules dépendances fonctionnelles élémentaires sont celles dans lesquelles une clé entière détermine un attribut.
Cette définition a le mérite d'être simple : pas de dépendance autre que K→A, K étant la clé et A un attribut non-clé. Il a été montré que toute relation a une décomposition en BCNF qui est sans perte. Par contre, une décomposition en BCNF ne préserve en général pas les DF. La figure XVII.32 illustre le cas typique où un attribut non-clé détermine une partie de clé, et indique le schéma de décomposition associé.
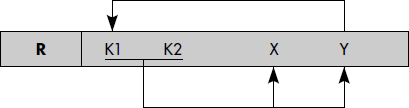
|
Une telle relation doit être décomposée en R1(K1, K2, X) et R2(Y, K1) |
Considérons par exemple la relation :
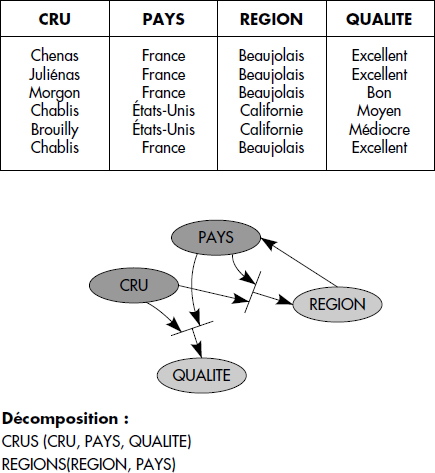
LOCALISATION (CRU, PAYS, REGION, QUALITE)avec les dépendances :
CRU, PAYS → REGION
CRU, PAYS → QUALITE
REGION → PAYS.Cette relation n'est pas en BCNF bien qu'en 3e forme puisque le cru ne détermine pas la région (il y a du Chablis en Bourgogne mais aussi en Californie ; notez que la qualité dépend bien du pays !). Une instance, le réseau de DF et la décomposition souhaitable sont représentés figure XVII.33. La DF CRU, PAYS → REGION est perdue. La décomposition est cependant sans perte.
XXII-7. QUATRIÈME ET CINQUIÈME FORMES NORMALES▲
La BCNF n'est pas suffisante pour éliminer complètement les redondances. Pour aller au-delà, il faut introduire des dépendances plus lâches. Nous allons en voir de plusieurs types.
XXII-7-1. DÉPENDANCES MULTIVALUÉES▲
Un exemple permet de comprendre la nature des redondances. Considérons la relation :
ETUDIANT (NE, COURS, SPORT)NE est le numéro d'étudiant, COURS les cours suivis et SPORT les sports pratiqués. Une extension de cette relation est représentée figure XVII.34. NE, COURS et SPORT constituent la clé composée. En effet, NE ne détermine ni cours ni sport, car il est conseillé de suivre plusieurs cours et de pratiquer plusieurs sports (c'est le cas de l'étudiant 100 ci-dessous).
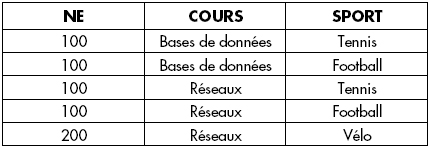
Ses redondances apparaissent clairement dans cette relation. Cependant, en raison de l'absence de dépendances fonctionnelles, elle est jusque-là non décomposable.
L'exemple précédent montre l'insuffisance de la notion de dépendance fonctionnelle : elle ne permet pas de saisir l'indépendance qui existe entre des attributs comme COURS suivi et SPORT pratiqué. Pour cela, on généralise la notion de DF en introduisant celle de dépendance multivaluée (DM) [Fagin77, Zaniolo81].
Notion XVII.14 : Dépendance multivaluée (Multivalued dependency)
Soit R (A1, A2… An) un schéma de relation, et X et Y des sous-ensembles de A1, A2, …, An. On dit que X ![]() Y (X multidétermine Y, ou il y a une dépendance multivaluée de Y sur X) si, étant données des valeurs de X, il y a un ensemble de valeurs de Y associées et cet ensemble est indépendant des autres attributs Z = R - X - Y de la relation R.
Y (X multidétermine Y, ou il y a une dépendance multivaluée de Y sur X) si, étant données des valeurs de X, il y a un ensemble de valeurs de Y associées et cet ensemble est indépendant des autres attributs Z = R - X - Y de la relation R.
Une dépendance multivaluée caractérise donc une indépendance entre deux ensembles d'attributs (Y et Z) corrélés par un même troisième X. Plus formellement, on a :
- (X
 Y) ⇔ {(x y z) et (x y' z') ∈ R ⇒ (x y' z) et (x y z') ∈ R}
Y) ⇔ {(x y z) et (x y' z') ∈ R ⇒ (x y' z) et (x y z') ∈ R}
où x, y, z, y', z' désignent des occurrences des attributs X, Y, Z, Y, Z.
Il faut souligner que les DF sont des cas particuliers de DM. En effet :
- (X → Y) ⇒ {(x y z) et (x y' z') ∈ R ⇒ y = y'}
Donc :
- (X → Y) ⇒ {(x y z) et (x y' z') ∈ R ⇒ (x y' z) et (x y z') ∈ R
Par suite :
- (X → Y) ⇒ (X
 Y)
Y)
Comme avec les dépendances fonctionnelles, il est possible d'effectuer des inférences à partir des dépendances multivaluées. Les axiomes d'inférence des DM sont les suivants, en considérant une relation composée d'un ensemble d'attributs R [Beeri79] :
- Complémentation : (X
 Y) ⇒ (X
Y) ⇒ (X  R - X - Y)
R - X - Y) - Augmentation : (X
 Y) et (V ⊆ W) ⇒ (XW
Y) et (V ⊆ W) ⇒ (XW  YV)
YV) - Transitivité : (X
 Y) et (Y
Y) et (Y  Z) ⇒ (X
Z) ⇒ (X  Z - Y)
Z - Y)
Des règles additionnelles s'en déduisent, telles que celle d'union :
- Union : (X
 Y) et (Y
Y) et (Y  Z) ⇒ (X
Z) ⇒ (X  YZ)
YZ)
À partir des axiomes précédents, il est possible d'introduire la notion de dépendance multivaluée élémentaire, ceci afin d'éliminer les dépendances déduites trivialement d'un ensemble de dépendances de base [Zaniolo81].
Notion XVII.15 : Dépendance multivaluée élémentaire (Elementary multivalued dependency)
Dépendance multivaluée X ![]() Y d'une relation R telle que :
Y d'une relation R telle que :
- Y n'est pas vide et est disjoint de X.
- R ne contient pas une autre DM du type X'
 Y' telle que X' ⊂ X et Y' ⊂ Y.
Y' telle que X' ⊂ X et Y' ⊂ Y.
Ainsi, une dépendance multivaluée élémentaire a, à la fois, un côté droit et un côté gauche minimaux, comme une dépendance fonctionnelle élémentaire.
Afin d'illustrer plus en détail, nous donnerons deux autres exemples de DM. Soit la relation :
VOL (NV, AVION, PILOTE)où NV est un numéro de vol. On suppose disposer d'un ensemble d'avions et d'un ensemble de pilotes. Tout pilote est conduit à piloter tout avion sur n'importe quel vol. Ainsi, les avions et les pilotes sont indépendants. D'où les deux DM élémentaires :
- NV
 AVION
AVION - NV
 PILOTE
PILOTE
Soit encore la relation :
PERSONNE (N°SS, PRENOM-ENFANT, N° VEHICULE)Il est clair que l'on a les DM élémentaires :
- N°SS
 PRENOM-ENFANT
PRENOM-ENFANT - N°SS
 N°VEHICULE
N°VEHICULE
XXII-7-1-1. QUATRIÈME FORME NORMALE▲
La quatrième forme normale est une généralisation de la forme normale de Boyce-Codd destinée à décomposer les relations ayant des DM élémentaires.
Notion XVII.16 : Quatrième forme normale (Fourth normal form)
Une relation est en quatrième forme normale si et seulement si les seules dépendances multivaluées élémentaires sont celles dans lesquelles une superclé détermine un attribut.
Rappelons qu'une superclé est un ensemble d'attributs contenant une clé. Donc, une relation R n'est pas en 4e FN si l'on peut trouver une dépendance de la forme X ![]() Y où X n'inclut pas une clé de R. Comme une dépendance fonctionnelle est un cas particulier de dépendance multivaluée, il apparaît qu'une relation en quatrième forme normale est en forme normale de Boyce-Codd et donc en troisième forme normale.
Y où X n'inclut pas une clé de R. Comme une dépendance fonctionnelle est un cas particulier de dépendance multivaluée, il apparaît qu'une relation en quatrième forme normale est en forme normale de Boyce-Codd et donc en troisième forme normale.
À titre d'exemple, la relation ETUDIANT (NE, COURS, SPORT) n'est pas en quatrième forme normale : la clé est l'ensemble des attributs et il existe des DM élémentaires entre des attributs participant à la clé :
- NE
 COURS
COURS - NE
 SPORT
SPORT
Il a été montré que toute relation a une décomposition (pas forcément unique) en quatrième forme normale qui est sans perte [Fagin77]. Par exemple, la relation ETUDIANT peut être décomposée en deux relations (NE, COURS) et (NE, SPORT) qui sont bien en quatrième forme normale.
XXII-7-1-2. DÉPENDANCES DE JOINTURE▲
La notion de dépendance multivaluée a conduit à décomposer les relations en quatrième forme normale. Est-ce suffisant pour éliminer les problèmes de redondances et anomalies ? [Nicolas78] et [Fagin79] ont montré que non.
Considérons par exemple la relation BUVCRU représentée figure XVII.35 ; cette relation modélise des vins bus par des buveurs, d'un cru donné et commandés à un producteur produisant ce cru.
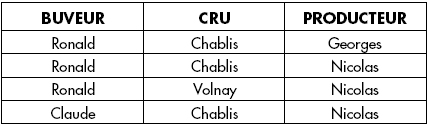
Cette relation est bien en quatrième forme normale. En effet, il n'existe pas de dépendance multivaluée d'après l'extension représentée ci-dessus :
- BUVEUR
 CRU est faux, car par exemple le tuple (Ronald Volnay Georges) n'existe pas.
CRU est faux, car par exemple le tuple (Ronald Volnay Georges) n'existe pas. - CRU
 PRODUCTEUR est faux, car par exemple le tuple (Claude Chablis Georges) n'existe pas.
PRODUCTEUR est faux, car par exemple le tuple (Claude Chablis Georges) n'existe pas. - PRODUCTEUR
 BUVEUR est faux, car par exemple le tuple (Claude Volnay Nicolas) n'existe pas.
BUVEUR est faux, car par exemple le tuple (Claude Volnay Nicolas) n'existe pas.
Autrement dit, si l'on considère les projections R1, R2, R3 de la relation BUVCRU sur deux attributs (voir figure XVII.36), on constate que l'on a :
- BUVCRU ≠ R1
 R2
R2 - BUVCRU ≠ R1
 R3
R3 - BUVCRU ≠ R2
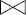 R3
R3
Cependant, la relation représentée figure XVII.35 présente bien des redondances : on apprend deux fois que Ronald boit du Chablis et que Nicolas produit du Chablis. Elle n'est cependant pas décomposable en deux relations.
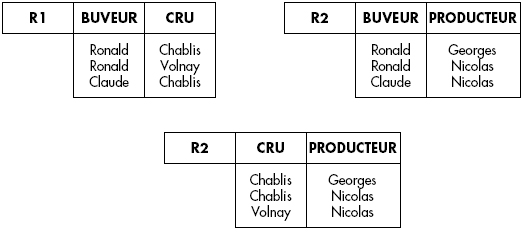
L'exemple précédent montre l'insuffisance de la notion de dépendance multivaluée pour éliminer les redondances. Le problème vient du fait que jusqu'à présent, nous avons essayé de décomposer une relation seulement en deux relations. Ainsi, la notion de dépendance multivaluée capture la possibilité de décomposer une relation en deux ; la relation (XYZ) dans laquelle X ![]() Y est en effet décomposée en (XY) et (XZ) puisque Y et Z sont indépendants par rapport à X. Comme nous allons le voir, il existe des relations non décomposables en deux mais décomposables en trois, quatre ou plus généralement N relations. Ce phénomène a été découvert par [Aho79] et [Nicolas78].
Y est en effet décomposée en (XY) et (XZ) puisque Y et Z sont indépendants par rapport à X. Comme nous allons le voir, il existe des relations non décomposables en deux mais décomposables en trois, quatre ou plus généralement N relations. Ce phénomène a été découvert par [Aho79] et [Nicolas78].
À titre d'exemple de relation décomposable en trois relations et non décomposable en deux, supposons que la relation BUVCRU de la figure XVII.35 obéisse à la contrainte d'intégrité assez plausible :
« Tout buveur ayant bu un cru et ayant commandé à un producteur produisant ce cru a aussi commandé ce cru à ce producteur ».
Cette contrainte s'écrit plus formellement :
- (b,c) ∈ R1 et (b,p) ∈ R2 et (c,p) ∈ R3 ⇒ (b,c,p) ∈ R
Dans ce cas, R sera la jointure de R1, R2 et R3 :
- R = R1
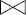 R2
R2 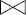 R3
R3
Cette contrainte est bien vérifiée par l'extension de la relation BUVCRU représentée figure XVII.35 en considérant ses projections R1, R2 et R3 représentées figure XVII.36.
Plus généralement, [Rissanen78] a introduit la notion de dépendance de jointure (DJ) afin de décomposer des relations en plusieurs.
Notion XVII.17 : Dépendance de jointure (Join dependency)
Soient R (A1, A2, …, An) un schéma de relation et R1, R2, …, Rm des sous-ensembles de {A1, A2, …, An}. On dit qu'il existe une dépendance de jointure *{R1, R2, …, Rm} si R est la jointure de ses projections sur R1, R2, …, Rm, c'est-à-dire si R = ????R1(R) ![]() ????R2(R)…
????R2(R)… ![]() ????Rm(R).
????Rm(R).
En d'autres termes, la dépendance de jointure *{R1, R2, …, Rm} est valide si R1, R2, …, Rp est une décomposition sans perte de R. En conséquence, une relation de schéma R satisfait la dépendance de jointure *{R1, R2, …, Rm} quand la condition suivante est valide pour toute instance r de R :
Si t1 ∈ ????R1(r) t2∈ ????R2(r)… …tm ∈ ????Rm(r), alors t1*t2*..tm ∈ R en notant * la jointure naturelle des relations Ri concernées.
Par exemple, la relation de schéma BUVCRU(BUVEUR, CRU, PRODUCTEUR) obéit à la dépendance de jointure :
*{(BUVEUR, CRU),(BUVEUR, PRODUCTEUR),(CRU, PRODUCTEUR)}Elle est donc décomposable en trois relations R1(BUVEUR,CRU), R2(BUVEUR, PRODUCTEUR) et R3(CRU, PRODUCTEUR) comme représenté figure XVII.36. Si (b, c), (b, p) et (c, p) sont respectivement des tuples de R1, R2 et R3, alors (b, c, p) est un tuple de BUVCRU.
Les dépendances multivaluées sont bien sûr des cas particuliers de dépendances de jointures. En effet, une relation R (X, Y, Z) vérifiant la dépendance multivaluée X ![]() Y (et donc X
Y (et donc X ![]() Z) satisfait la dépendance de jointure *{(XY), (XZ)}.
Z) satisfait la dépendance de jointure *{(XY), (XZ)}.
XXII-7-1-3. CINQUIÈME FORME NORMALE▲
La forme normale de projection jointure, parfois appelée cinquième forme normale, est une généralisation de la quatrième à partir de la notion de dépendance de jointure. Sa définition nécessite d'étudier les dépendances de jointures comme nous l'avons fait pour les DF ou les DM. Soit une relation R et *{R1, R2…Rp} une dépendance de jointure. Une telle dépendance de jointure est triviale si l'une des relations Ri est la relation R elle-même.
Il nous est maintenant possible de définir la forme normale de projection-jointure, encore appelée 5e forme normale.
Notion XVII.18 : Forme normale de projection-jointure (Project-join normal form)
Une relation R est en forme normale de projection-jointure si et seulement si toute dépendance de jointure est triviale ou tout Ri est une superclé de R (c'est-à-dire que chaque Ri contient une clé de R).
L'idée simple est que si la DJ est impliquée par les clés, la décomposition n'éliminera pas de redondance et est sans intérêt. Si elle contient R, elle ne sert à rien puisque R demeure. Dans les autres cas, il est possible de décomposer par projection selon les schémas de la DJ ; l'expression de jointures dérivées de la DJ permet de recomposer la relation R. Par suite, la décomposition d'une relation non en 5e forme suit les DJ et est sans perte. Par contre, elle ne préserve en général pas les DF, comme la BCNF. Notons aussi que la 5e forme normale est une généralisation directe de la BCNF et de la 4e ; donc une relation en 5e forme est en 4e et bien sûr en 3e.
Ainsi la relation BUVCRU n'est pas en 5e forme normale puisque la seule clé candidate (BUVEUR, CRU, PRODUCTEUR) n'implique pas la DJ *{(BUVEUR CRU), (CRU PRODUCTEUR), (BUVEUR PRODUCTEUR)}. Elle doit donc être décomposée en ces trois relations afin d'éviter les anomalies de mise à jour.
[Fagin79] a démontré le résultat essentiel suivant. Toute relation en 5e forme normale ne peut plus être décomposée sans perte d'informations (excepté par les décompositions basées sur les clés qui sont sans intérêt) si l'on ne considère que la décomposition par projection et la recomposition par jointure. La 5e forme normale est donc un point final à la décomposition par projection-jointure. Voilà pourquoi Fagin a proposé d'appeler cette forme « forme normale de projection-jointure » (JD/NF).
La 5e forme n'est cependant pas la forme ultime de décomposition si l'on accepte aussi des décompositions horizontales, c'est-à-dire en partitionnant la table en sous-tables comportant chacune un ensemble de tuples avec tous les attributs. Il est possible d'introduire des dépendances algébriques du style R ⊂ E(R) où E est une expression de l'algèbre relationnelle avec union, projection et jointure [Yannakakis80]. Les dépendances d'inclusion constituent une forme plus restreinte de dépendances qui unifient les DF et les DJ [Abiteboul95]. Mais tout cela n'est pas d'une grande utilité pour concevoir une BD.
XXII-7-2. CONCEPTION DU SCHÉMA INTERNE▲
Nous abordons dans cette partie les problèmes plus pratiques de passage au niveau interne, c'est-à-dire d'implémentation du schéma logique sur un SGBD particulier.
XXII-7-2-1. LES PARAMÈTRES À PRENDRE EN COMPTE▲
La conception du schéma interne, encore appelée conception physique, vise non plus à résoudre les problèmes sémantiques, mais les problèmes de performances. L'objectif est, pour une charge applicative donnée, de trouver le meilleur schéma physique pour optimiser les temps d'accès et de calcul, plus généralement le débit en transactions et les temps de réponse.
Quels sont les paramètres nécessaires ? Tout d'abord, le schéma logique de la base issu des étapes précédentes est connu. Pour chaque relation, il faut aussi connaître les tailles en nombre de tuples et le profil moyen d'un tuple (attributs et tailles). En plus, il faut avoir un modèle de l'application. Plus précisément, pour chaque transaction, il est souhaitable de connaître :
- la fréquence, voire éventuellement une distribution de fréquence pendant la journée ;
- les requêtes exécutées, avec les types (SELECT, UPDATE, etc.), les critères et un nombre de fois si la requête est répétée ;
- le mode d'exécution, c'est-à-dire requête interactive ou compilée.
À partir de ces paramètres, un modèle de l'application peut être élaboré. Il peut être analytique ou simulé. Mais il faut aussi modéliser le SGBD sauf si l'on choisit un modèle simulé effectivement construit sur le SGBD. Les paramètres intéressants à prendre en compte au niveau du SGBD sont les configurations des disques, la taille du cache, la taille des pages, les temps de lecture et d'écriture d'une page, les types d'index, etc. C'est en fait très complexe.
Le modèle analytique conduit à une formule de coût paramétrée (par exemple la présence ou non d'un index est un paramètre) qu'il s'agit d'optimiser. En général, le coût va être composé du temps d'entrées-sorties et du temps unité centrale pondéré par un coefficient unificateur. Les formules de l'optimiseur de requêtes sont à intégrer dans un tel modèle. Le problème est généralement que le nombre de paramètres est trop grand pour permettre une recherche d'optimum.
Le modèle simulé est plus crédible. Il conduit à réaliser une base réduite avec des corps de transactions comprenant essentiellement les requêtes. Un générateur de transactions doit alors être réalisé pour simuler la charge. Un tel modèle permet de faire des mesures effectives en faisant varier tel ou tel paramètre, par exemple en ajoutant ou en supprimant un index. Les modèles à base d'outils généraux basés sur les files d'attente sont aussi utilisables.
Au-delà du modèle qui est un problème en soi, nous examinons ci-dessous les paramètres sur lesquels l'administrateur système peut jouer. Ceux-ci sont souvent dépendants du SGBD.
XXII-7-2-2. DÉNORMALISATION ET GROUPEMENT DE TABLES▲
D'un point de vue logique, pour éviter anomalies et pertes d'opérations, nous avons vu ci-dessus qu'il était souhaitable de décomposer les relations par projection, la recomposition étant faite par jointure. D'un point de vue performance, ce n'est pas toujours optimal. En effet, la normalisation conduit, si l'application le nécessite, à recalculer les jointures. D'où l'idée d'une étape de dénormalisation possible.
Notion XVII.19 : Dénormalisation (Denormalisation)
Technique consistant à implémenter la jointure de deux relations (ou plus) à la place des relations individuelles initiales.
Bien sûr, la dénormalisation conduit à des redondances et éventuellement à des valeurs nulles qui doivent être prises en compte par les programmes d'application. Soulignons aussi que les jointures intéressantes suivent en général les contraintes référentielles, qui sont les plus fréquemment utilisées. Quand une dénormalisation est-elle souhaitable ? Pratiquement, le gain est pour les recherches, la jointure des deux tables étant remplacée par une sélection sur la table résultant de la jointure. La perte affecte les mises à jour qui s'appliquent sur la table jointure en plusieurs points, mais aussi les sélections sur les tables individuelles qui doivent maintenant s'appliquer sur la jointure. Seuls un calcul analytique ou une simulation permettent de calculer la différence et de conclure.
Une variante plus performante de la dénormalisation est le groupement, permis dans certains SGBD.
Notion XVII.20 : Groupement (Clustering)
Technique permettant de regrouper dans une même page ou des pages voisines les tuples de deux tables (ou plus) selon un critère de jointure.
Cette technique est connue depuis longtemps sous le nom de placement à proximité dans le modèle réseau. Elle permet par exemple de placer les lignes de commandes dans la page de l'en-tête. Ainsi, la jointure ne nécessite qu'une entrée-sortie par commande. Il n'y a cette fois pas de duplication et donc pas de problème introduit en mise à jour. C'est donc une excellente technique qui peut cependant pénaliser les sélections sur l'une et l'autre des tables.
XXII-7-2-3. PARTITIONNEMENT VERTICAL ET HORIZONTAL▲
Le partitionnement vertical consiste à diviser la table en deux par projection en répétant les clés.
Notion XVII.21 : Partitionnement vertical (Vertical partitionning)
Technique consistant à implémenter deux projections ou plus d'une table sur des schémas R1, R2… en répétant la clé dans chaque Ri pour pouvoir recomposer la table initiale par jointure sur clé.
Cette technique, qui prolonge en quelque sorte la normalisation, permet d'éloigner d'une relation tous les attributs peu fréquemment utilisés : ceux-ci sont reportés dans la deuxième table. La table fréquemment sélectionnée R1 devient plus petite, ce qui améliore les performances. La technique est donc très intéressante si un groupe d'attributs longs est rarement interrogé. Là encore, calculs analytiques et simulations aideront à prendre les bonnes décisions.
Le partitionnement horizontal consiste au contraire à diviser la table en sous-tables de même schéma, chacune conservant une partie des tuples.
Notion XVII.22 : Partitionnement horizontal (Horizontal partitionning)
Technique consistant à diviser une table en N sous-tables selon des critères de restriction σ1, σ2, …, σn.
Tout tuple respectant les contraintes d'intégrité doit appartenir à l'une des partitions. Un exemple typique est la création de partitions sur le mois pour la table des commandes. Ainsi, douze partitions sont créées, une par mois. Cette technique est particulièrement intéressante si les requêtes indiquent souvent le mois de la commande, donc en général un des σi. Elle permet surtout de diviser les grosses tables notamment pour le chargement et la sauvegarde. De nombreux SGBD l'implémentent de manière invisible au développeur d'application. Le partitionnement horizontal correspond de fait à une décomposition par union.
XXII-7-2-4. CHOIX DES INDEX▲
Le choix des index n'est pas un problème simple. En effet, les index permettent des gains impressionnants en interrogation, mais des pertes significatives en mise à jour. De plus, il existe différents types d'index, les plus fréquents étant les arbres B et les index bitmap pour l'OLAP.
Alors que faire ? Quelques règles simples sont utiles :
- Toute clé primaire doit être indexée par un arbre B dès que la relation dépasse quelques pages. Cela évite les problèmes pour la vérification d'intégrité, la recherche sur clé, etc. Les SGBD du marché automatisent de plus en plus ce type d'indexation.
-
Un attribut sur lequel figure un prédicat conjonctif avec égalité sera indexé :
- par un arbre B si le nombre de valeurs possibles dépasse quelques centaines ;
- par un index bitmap sinon.
Il ne faut cependant pas abuser de l'indexation pour les tables fréquemment mises à jour ou avec insertions nombreuses. Dans ce cas, un modèle analytique ou une simulation permettront d'y voir plus clair. On pourra consulter [Cardenas75, Schkolnick85] pour de tels modèles.
XXII-7-2-5. INTRODUCTION DE VUES CONCRÈTES▲
Mentionnons pour finir que l'introduction de vues concrètes précalculant les réponses aux questions fréquentes est une technique très intéressante pour l'optimisation. Elle est d'ailleurs de plus en plus utilisée dans les environnements OLAP, comme nous l'avons vu au chapitre IX traitant des vues. Bien sûr, les répercussions des mises à jour des relations de base sur la vue concrète peuvent être difficiles. Une vue concrète sera donc particulièrement intéressante lorsque les relations de base sont peu fréquemment mises à jour.
XXII-7-3. CONCLUSION▲
En résumé, concevoir une base de données nécessite tout d'abord d'élaborer un schéma conceptuel. Le modèle objet et le langage graphique de modélisation UML nous semblent un bon véhicule pour ce faire. À partir de là, des règles précises permettent d'obtenir un schéma logique relationnel. Faut-il ensuite normaliser les schémas de tables ? Cela peut être utile en cas de mauvaise isolation des entités. Cependant, la normalisation est un processus long qui nécessite d'analyser les dépendances qu'on n'applique finalement qu'à l'exception. Trop systématiquement appliquée, elle conduit à éclater les tables en molécules de quelques attributs. Il apparaît alors des myriades de tables qu'il faut regrouper. L'optimisation est finalement beaucoup plus importante pour les performances, mais très difficile à maîtriser. C'est un métier de spécialiste de système.
La conception reste encore plus un art qu'une science, surtout avec le modèle objet. En effet, on est à peu près incapable de dire ce qu'est un bon schéma objet. De plus, le passage d'un schéma objet à un schéma « logique » objet-relationnel reste une étape mal maîtrisée. Les approches par un modèle sémantique de plus haut niveau sont très intéressantes [Bouzeghoub91], mais restent théoriques. Il y a donc toujours de grands besoins en recherche sur la conception, notamment avec l'avènement des bases de données objet-relationnelles. La mode est plutôt aujourd'hui aux méthodes de conception globale pour les applications objet. Reste qu'il faut bien générer le schéma de la base. Les patterns, bibliothèques de cas typiques paramétrables, sont sans doute une voie d'avenir [Gamma97].
XXII-7-4. BIBLIOGRAPHIE▲
[Abiteboul95] Abiteboul S., Hull R., Vianu V., Foundations of Databases, Addison-Wesley, 1995.
- Ce livre sur les fondements des bases de données couvre particulièrement bien la théorie des dépendances fonctionnelles, de jointure et d'inclusion, et bien d'autres aspects.
[Aho79] Aho A.V., Beeri C., Ullman J-D., « The Theory of Joins in Relational Databases », ACM Transactions on Database Systems, Vol.4, n° 3, p. 297-314, Sept. 1979.
- Cet article étudie la décomposition d'une relation par projection et donne des algorithmes efficaces pour déterminer si la jointure de relations est sans perte en présence de dépendances fonctionnelles et multivaluées.
[Armstrong74] Amstrong W.W., « Dependency Structures of Database Relationships », IFIP World Congress, North-Holland Ed., p. 580-583, 1974.
- Cet article introduit les fameux axiomes de Armstrong.
[Batini86] Batini C., Lenzerini M., « A Methodology for Data Schema Integration in the Entity-Relationship Model », IEEE Transactions on Software Engineering, vol. 10, n° 6, p.650-664, Nov. 1984.
- Les auteurs présentent une méthodologie pour intégrer les schémas entité-association.
[Beeri79] Beeri C., Bernstein P.A., « Computational Problems Related to the Design of Norma Form Schemas », ACM Transactions on Database Systems, Vol.4, n° 1, Mars 1979.
- Cet article décrit un algorithme linéaire pour tester si une dépendance fonctionnelle est dans la fermeture d'un ensemble de DF et une implémentation optimisée de l'algorithme de synthèse de Bernstein.
[Benci76] Benci E., « Concepts for the Design of a Conceptual Schema », IFIP Conference on Modelling in Database Management Systems, North-Holland Ed., p. 181-200, 1976.
- Cet article collectif introduit une méthode de type entité-association pour modéliser des données au niveau conceptuel. C'est un des articles fondateurs de MERISE.
[Bernstein76] Bernstein P.A., « Synthesizing Third Normal Form Relations from Functional Dependencies », ACM Transactions on Database Systems, Vol.1, n° 4, p. 277-298, 1976.
- L'auteur présente l'algorithme de synthèse de relations en 3e FN et ses fondements.
[Bouzeghoub85] Bouzeghoub M., Gardarin G., Métais E., « SECSI: An Expert System for Database Design », 11th Very Large Data Base International Conference, Morgan Kaufman Pub., Stockolm, Suède, 1985.
- Cet article décrit le système SECSI basé sur un modèle sémantique appelé MORSE. MORSE supporte l'agrégation, la généralisation, l'association et l'instanciation. SECSI est construit selon une architecture système expert. C'est un outil d'aide à la conception de bases de données relationnelles qui transforme le modèle sémantique en relations normalisées. Pour passer au relationnel, SECSI applique les règles de transformation du modèle objet vues ci-dessus.
[Bouzeghoub91] Bouzeghoub M., Métais E., « Semantic Modeling of Object Oriented Databases », Proc. of the 17th Intl. Conf. on Very large Data Bases, Morgan Kaufman Ed., p. 3-14, Sept. 1991.
- Cet article propose une méthode de conception de BD objet basée sur un réseau sémantique. La méthode a été implémentée dans un outil CASE.
[Bouzeghoub97] Bouzeghoub M., Gardarin G., Valduriez P., Les Objets, Éditions Eyrolles, Paris, 1997.
- Ce livre couvre tous les aspects de l'objet et détaille les principales méthodologies de conception objet.
[Chen76] Chen P.P., « The Entity-Relationship Model - Toward a Unified View of Data », ACM Transactions on Database Systems, Vol.1, n° 1, p. 9-36, Mars1976.
- Le fameux article introduisant le modèle E/R.
[Codd71] Codd E.F., « Normalized Database structure : A Brief Tutorial », ACM SIGFIDET Workshop on Data Description, Access and Control, p. 1-17, Nov. 1971.
- Un état de l'art sur les trois premières formes normales.
[Codd72] Codd E.F., « Further Normalization of the Data Base Relational Model », in Data Base Systems, R. Rusin ed., Prentice-Hall, 1972.
- Cet article introduit la BCNF. L'intérêt de cette forme normale fut plus tard contesté par Bernstein.
[Codd74] Codd E.F., « Recent Investigations in Relational Database Systems », IFIP World Congress, North Holland Ed., p. 1017-1021, 1974.
- Un autre tutoriel sur le relationnel et les formes normales.
[DeAntonellis83] De Antonellis V., Demo B., « Requirements Collection and analysis » in Methodology and Tools for Database Design, S. Ceri ED., North-Holland, 1983.
- Cet article fait le tour de méthodes en matière de capture des besoins des utilisateurs.
[Delobel73] Delobel C., Casey R.G., « Decomposition of a Data Base and the Theory of Boolean Switching Functions », IBM Journal of research and Devlopment, vol. 17, n° 5, p. 374-386, 1973.
- Cet article étudie les dépendances fonctionnelles comme des fonctions booléennes. Il introduit en particulier la notion de couverture minimale.
[Fagin77] Fagin R., « Multivalued Dependencies and a New Normal Form for Relational Databases », ACM Transactions on Database Systems, Vol.2, n° 3, p. 262-278, Sept. 1977.
- Cet article introduit les dépendances multivaluées et la 4e forme normale.
[Fagin79] Fagin R., « Normal Forms and Relational Database Operators », Proc. ACM SIGMOD Intl. Conf. on Management of Data, Boston, p.153-160, Juin 1979.
- Cet article introduit les dépendances de jointures et la forme normale par projection jointure.
[Fagin81] Fagin R., « A Normal Form for Relational Databases Based on Domains and Keys », ACM Transactions on Database Systems, vol. 6, n° 3, p. 387-415, Sept. 1981.
- Cet article introduit une nouvelle forme normale basée sur des définitions de domaines, les déclarations de clés et des contraintes généralisées exprimées par des règles logiques. Cette forme généralise les précédentes.
[Gamma97] Gamma E., Helm R., Johnson R., Vlissides J., Design Patterns, Addisson-Wesley, Professional Computing Series, 1997.
- Ce livre définit ce qu'est un pattern objet pour la conception et présente plus d'une vingtaine de patterns utiles.
[Hammer93] Hammer M., Champy J., Le Reengineering, Dunod, 1993.
- Ce livre détaille les techniques de reengineering, en particulier le BPR qui permet de modéliser une société depuis le client jusqu'au processus de fabrication avec des diagrammes de flux d'information.
[Kettani98] Kettani N., Mignet D., Paré P., Rosenthal-Sabroux C., De Merise à UML, Éd. Eyrolles, Paris, 998
- Ce livre présente UML, le langage de modélisation universel, le compare avec MERISE et propose une démarche de transition.
[Métais97] Métais E., Kedad Z., Comyn-Wattiau I., Bouzeghoub M., « Using Linguistic Knowledge in View Integration : Towards a Third Generation of Tools », Data and Knowledge Engineering, Nort-Holland, 1997.
- Cette article propose une méthodologie d'intégration de vues fondée sur des connaissances linguistiques. Un outil d'intégration pouvant utiliser une ontologie en est dérivé.
[Muller98] Muller P.A., Modélisation Objet avec UML, Éd. Eyrolles, Paris, 1998.
- Ce livre présente l'objet et le langage de modélisation associé UML. Il propose quelques exemples de modèles.
[Navathe84] Navathe S., El-Masri R., Sahidar T., « Relationship Merging in Schema Integration », Proc. 10th Intl. Conf. on Very Large Data Bases, Morgan Kaufman Ed., p. 78-90, Florence, Août 1984.
- Cet article propose des méthodes d'intégration de schémas, notamment de fusion d'associations dans un modèle E/R.
[Nicolas78] Nicolas J-M., « Mutual Dependencies and Some Reults on undecomposable relations », Proc. 5th Intl. Conf. on Very Large Data Bases, IEEE Ed., p. 360-367, Berlin, 1978.
- Cet article propose des dépendances mutuelles intermédiaires entre les dépendances multivaluées et de jointure. Il montre que des relations non décomposables en 2 peuvent l'être en 3.
[Rational98] Rational Soft., UML 1.1, Documentation du langage UML, http://www.rational.com/uml/.
- La documentation en HTML et PDF de UML.
[Rissanen73] Rissanen J., Delobel C., « Decomposition of Files - A Basis for Data Storage and Retrieval », IBM Research Report RJ 1220, San José, Ca., Mai 1973.
- Quelques-uns des premiers algorithmes de décomposition en 3e forme normale.
[Rissanen78] Rissanen J., « Theory of Relations for Databases - A Tutorial Survey », 7th Symposium on Math. Foundations of Computer Science, Springer- Verlag ED., LCNS n° 64, p. 537-551, 1978.
- Un tutoriel sur la décomposition des relations, de la 1e à la 4e forme normale.
[Tardieu83] Tardieu H., Rochefeld A., Colletti R., La Méthode Merise, Éd. d'Organisations, 1983.
- Le livre de base sur la méthode MERISE.
[Ullman88] Ullman J.D., Principles of database and Knowledge-base Systems, vol. I, Computer Science Press, Rockville, MD, 1988.
- Le livre de Ullman couvre particulièrement bien la théorie de la décomposition et les dépendances généralisées par des tableaux.
[WonKim95] Won Kim, Choi I., Gala S., Scheevel M., « On Resolving Schematic Heterogeneity in Multidatabase systems », in Modern Database Systems, Won Kim ED., ACM Press, 1995.
- Cet article est un tutoriel des techniques de résolution de conflits entre schémas à intégrer. Il discute particulièrement de l'intégration de schémas objet et relationnels dans un contexte de BD réparties fédérées.
[Yannakakis80] Yannakakis M., Papadimitriou C.H., « Algebraic dependencies », Foundations of Computer Science Conference, IEEE Ed., p. 328-332, 1980.
- Cet article introduit les dépendances algébriques qui généralisent les dépendances de jointures.
[Zaniolo81] Zaniolo C., Melkanoff M.A., « On the design of relational Database Schemata », ACM Transactions on Database Systems,Vol.6, n° 1, p. 1-47, 1981.
- Cet article introduit la 4e forme normale et des algorithmes de normalisation basés sur des hypergraphes.