Cours complet pour apprendre les systèmes de gestion de bases de données

Pourquoi des vues ? Elles permettent de réaliser, dans le monde des SGBD relationnels, le niveau externe des SGBD selon l'architecture ANSI/SPARC. Rappelons que le niveau externe propose à l'utilisateur une perception de la base plus proche de ses besoins, en termes de structures et de formats de données. De manière générale, les vues garantissent une meilleure indépendance logique des programmes par rapport aux données. En effet, le programme restera invariant aux modifications de schéma s'il accède à la base via une vue qui l'isole de celle-ci. Lors des modifications du schéma de la base, l'administrateur modifiera seulement la définition des vues, et les programmes d'application pourront continuer à travailler sans modification. Les vues ont aussi un rôle de sécurité : l'utilisateur ne peut accéder qu'aux données des vues auxquelles il a droit d'accès ; ainsi, les données en dehors de la vue sont protégées. De manière détournée, les vues permettent aussi certains contrôles d'intégrité lorsqu'elles sont utilisées pour les mises à jour : on dit alors qu'on effectue une mise à jour au travers d'une vue. De telles mises à jour sont très contrôlées, comme nous le verrons ci-dessous.

Ces dernières années, les vues ont trouvé de nouvelles applications. Elles permettent de définir des tables virtuelles correspondant aux besoins des programmes d'application en termes de données. Dans le monde du client-serveur, les vues constituent un élément essentiel d'optimisation de performances. Par exemple, la définition d'une vue jointure de deux tables, ou résultant d'un calcul d'agrégat, évite au client les risques de lire les tuples des tables et de faire le calcul de jointure ou d'agrégat sur le client : seules les données résultant du calcul de la vue sont exportées sur le site client. On laisse ainsi faire au serveur les calculs de jointure, agrégats, etc., qu'il sait en principe bien faire. Dans le monde des entrepôts de données et du décisionnel, les vues peuvent être concrétisées. Elles permettent de réaliser par avance des cumuls ou synthèses plus sophistiqués de quantités extraites de la base selon plusieurs dimensions. Des mécanismes de mises à jour des vues concrètes lors des mises à jour des relations de base sont alors développés afin d'éviter le recalcul des cumuls.

Les vues ont donc une importance croissante dans les bases de données. En pratique, ce sont des relations virtuelles définies par des questions. Cette définition est stockée dans la métabase. Les vues sont interrogées comme des relations normales. Idéalement, elles devraient pouvoir être mises à jour comme des relations normales. Les vues concrètes sont calculées sur disques lors de leurs créations. Des mécanismes de mise à jour différentiels permettent le report efficace des mises à jour des relations de base. Toutes ces techniques sont aujourd'hui bien maîtrisées ; nous allons les présenter ci-dessous.

Afin d'illustrer les mécanismes de vues, nous utiliserons tout d'abord la base de données viticole classique composée des relations :

BUVEURS (NB, NOM, PRENOM, ADRESSE, TYPE)
         VINS (NV, CRU, REGION, MILLESIME, DEGRE)
         ABUS (NV, NB, DATE, QUANTITÉ).

décrivant respectivement les buveurs, les vins, et les consommations de vins quotidiennes. Comme habituellement, les clés des relations sont soulignées. Des vues typiques sont les vins de Bordeaux, les gros buveurs, les quantités de vins bues par crus, etc.

Pour des exemples plus avancés, intégrant notamment des agrégats complexes, nous utiliserons la base MAGASINS suivante :

VENTES(NUMV, NUMPRO, NUMFOU, DATE, QUANTITÉ, PRIX)
       PRODUITS (NUMPRO, NOM, MARQUE, TYPE,PRIX)
       FOURNISSEURS (NUMFOU, NOM, VILLE, RÉGION, TELEPHONE)

Des vues typiques sont les quantités de produits vendus par fournisseur et par mois, les évolutions des quantités commandées par région, etc. La relation Ventes décrit les ventes journalières de produits. NUMPRO est la clé de produits et NUMFOU celle de fournisseurs. Dans une telle base de données, les faits de base sont les ventes, alors que produits et fournisseurs constituent des dimensions permettant d'explorer les ventes selon une ville ou une région par exemple.

Ce chapitre est organisé comme suit. Après cette introduction, la section 2 expose plus formellement le concept de vue, détaille le langage de définition et présente quelques exemples simples de vues. La section 3 développe les mécanismes d'interrogation de vues. La section 4 pose le problème de la mise à jour des vues et isole les cas simples tolérés par SQL. La section 5 traite des vues concrètes, notamment pour des applications décisionnelles. En particulier, les techniques de report des mises à jour depuis les relations de base sur des vues concrètes avec agrégats sont étudiées. La conclusion évoque quelques autres extensions possibles du mécanisme de gestion des vues.

Dans cette partie, nous définissons tout d'abord précisément ce qu'est une vue, puis nous introduisons la syntaxe SQL pour définir une vue.

Une vue est donc un ensemble de relations déduites d'une base de données, par composition des relations de la base. Le schéma de la vue est un schéma externe au sens ANSI/SPARC. Dans la norme SQL, la notion de vue a été réduite à une seule relation déduite. Une vue est donc finalement une table virtuelle calculable par une question.

La syntaxe générale de la commande SQL1 de création de vue est :

CREATE VIEW <NOM DE VUE> [ (LISTE D'ATTRIBUT)]
        AS <QUESTION>
        [WITH CHECK OPTION]

Le nom de vue est le nom de la table virtuelle correspondant à la vue, la liste des attributs définit les colonnes de la table virtuelle, la question permet de calculer les tuples peuplant la table virtuelle. Les colonnes du SELECT sont appliquées sur celles de la vue. Si les colonnes de la vue ne sont pas spécifiées, celle-ci hérite directement des colonnes du SELECT constituant la question.

La clause WITH CHECK OPTION permet de spécifier que les tuples insérés ou mis à jour via la vue doivent satisfaire aux conditions de la question définissant la vue. Ces conditions seront vérifiées après la mise à jour : le SGBD testera que les tuples insérés ou modifiés figurent bien dans la réponse à la question, donc dans la vue. Ceci garantit que les tuples insérés ou modifiés via la vue lui appartiennent bien. Dans le cas contraire, la mise à jour est rejetée si la clause WITH CHECK OPTION est présente. Par exemple, si la vue possède des attributs d'une seule table et la question un critère de jointure avec une autre table, les tuples insérés dans la table correspondant à la vue devront joindre avec ceux de l'autre table. Ceci peut être utilisé pour forcer la vérification d'une contrainte référentielle lors d'une insertion via une vue. Nous étudierons plus en détail la justification de cette clause dans la partie traitant des mises à jour au travers de vues.

La suppression d'une vue s'effectue simplement par la commande :

DROP <NOM DE VUE>

Cette commande permet de supprimer la définition de vue dans la métabase (aussi appelée catalogue) de la base. En principe, sauf comme nous le verrons ci-dessous, dans le cas des vues concrètes, une vue n'a pas d'existence physique : c'est une fenêtre dynamique (et déformante), non matérialisée sur les disques, par laquelle un utilisateur accède à la base. La destruction de vue n'a donc pas à se soucier de détruire des tuples.

Voici maintenant quelques exemples de définition de vues. Soit la base de données Viticole dont le schéma a été rappelé en introduction.

• (V1) Les vins de Bordeaux :

CREATE VIEW VINSBORDEAUX (NV, CRU, MILL, DEGRÉ)
AS SELECT NV, CRU, MILLÉSIME, DEGRÉ
FROM VINS
WHERE RÉGION = "BORDELAIS".

Cette vue est simplement construite par une restriction suivie d'une projection de la table Vins. Chaque tuple de la vue est dérivé d'un tuple de la table Vins.

• (V2) Les gros buveurs :

CREATE VIEW GROSBUVEURS
AS SELECT NB, NOM, PRÉNOM, ADRESSE
FROM BUVEURS B, ABUS A
WHERE B.NB = A.NB AND A.QUANTITÉ > 10
WITH CHECK OPTION

Un tuple figure dans la vue GrosBuveurs si le buveur correspondant a commis au moins un abus en quantité supérieure à 10 verres. C'est là une définition très large des gros buveurs. La définition de vue comporte une restriction et une jointure. La clause WITH CHECK OPTION précise que lors d'une insertion d'un buveur via la vue, on doit vérifier qu'il s'agit bien d'un gros buveur, c'est-à-dire que le buveur a déjà commis un abus de quantité supérieure à 10. Notez que ceci spécifie une règle d'intégrité référentielle à l'envers pour les gros buveurs, ce qui est paradoxal.

• (V3) Les quantités de vins bues par crus :

CREATE VIEW VINSBUS (CRU, MILL, DEGRÉ, TOTAL)
AS SELECT CRU, MILLÉSIME, DEGRÉ, SUM(QUANTITÉ)
FROM VINS V, ABUS A
WHERE V.NV = A.NV
GROUP BY CRU

Cette vue fait appel à une jointure (suivant une contrainte référentielle) suivie d'un calcul d'agrégat (la somme). Un tuple de la table Vins donne plusieurs tuples lors de la jointure (autant qu'il y a d'abus) ; ceux-ci sont ensuite regroupés selon le cru.

Pour la base MAGASINS, nous définirons seulement une vue (V4) documentant la table VENTES selon les « dimensions » PRODUITS et FOURNISSEURS, résultant de jointures sur clé de ces tables :

CREATE VIEW VENTEDOC (NUMV,NOMPRO,MARQUE,NOMFOU,VILLE,RÉGION, DATE,
QUANTITÉ, PRIX) AS
SELECT V.NUMV,P.NOM,P.MARQUE,F.NOM,F.VILLE,F.RÉGION,V.DATE,
V.QUANTITÉ, V.PRIX
FROM VENTES V, PRODUITS P, FOURNISSEURS F
WHERE V.NUMPRO=P.NUMRO AND V.NUMFOU=F.NUMFOU

Nous verrons des vues plus complexes, notamment avec des agrégats ci-dessous.

La suppression des vues ci-dessus s'effectuera par les commandes :

DROP VINSBORDEAUX
DROP GROSBUVEURS
DROP VINBUS
DROP VENTESDOC

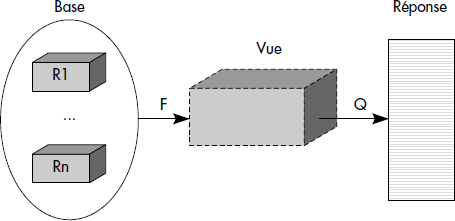
Du point de vue de l'utilisateur, l'interrogation au travers d'une vue s'effectue comme pour une table normale. Le rôle du serveur est alors d'enrichir la question avec la définition de vue qu'il retrouve dans la métabase. Plus formellement, la définition d'une vue V sur des relations R1, R2…Rn est une fonction V = F(R1, R2…Rn), où F est une expression de l'algèbre relationnelle étendue avec des agrégats. F est donc une expression de restriction, projection, jointure, union, différence et agrégat. Une question Q est exprimée sur la vue en SQL. Il s'agit aussi d'une fonction calculant la réponse R = Q(V), où Q est aussi une expression de l'algèbre relationnelle étendue. Calculer R à partir de la base revient donc à remplacer V dans la requête R = Q(V) par sa définition. On obtient alors la fonction composée :

R = Q(F(R1, R2…Rn)).

Ce mécanisme est illustré figure IX.1. La requête résultante peut alors être passée à l'optimiseur et le plan d'exécution correspondant peut être calculé. C'est ainsi que fonctionnent les SGBD : ils génèrent la requête composition de la définition de vue et de la requête usager, et traitent ensuite cette requête plus complexe, mais évaluable sur les relations de la base.

Deux techniques sont possibles pour réaliser la composition de la vue et de la requête utilisateur : la transformation de la requête source appelée modification de question, ou la transformation relationnelle de l'arbre, parfois appelée concaténation d'arbre.

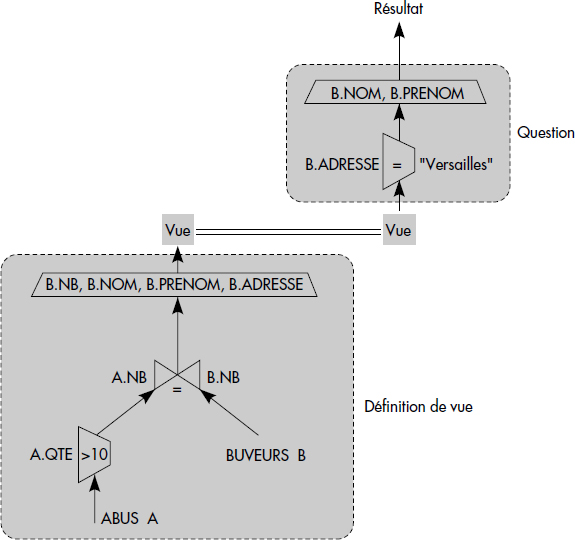
La modification de question est une technique inventée dans le projet Ingres à Berkeley [Stonebraker75]. Elle permet de remplacer les vues par leurs définitions lors des recherches ou d'ajouter des prédicats afin de vérifier des propriétés avant d'exécuter une requête. La figure IX.2 illustre cette technique pour la recherche des gros buveurs habitant à Versailles. Cette technique peut aussi être utilisée pour les mises à jour afin d'enrichir le critère pour vérifier par exemple la non-violation de contraintes d'intégrité.

SELECT NOM, PRÉNOM
FROM GROSBUVEURS
WHERE ADRESSE LIKE "VERSAILLES".

CREATE VIEW GROSBUVEURS
AS SELECT NB, NOM, PRÉNOM, ADRESSE
FROM BUVEURS B, ABUS A
WHERE B.NB = A.NB AND A.QUANTITÉ > 10.

SELECT NOM, PRÉNOM
FROM BUVEURS B, ABUS A
WHERE B.ADRESSE LIKE "VERSAILLES" AND B.NB=A.NB AND A.QUANTITÉ > 10.

La concaténation d'arbres est une technique inventée dans le fameux système R à San José [Astrahan76]. La définition de vue se retrouve dans la métabase sous la forme d'un arbre relationnel. L'arbre résultant de l'analyse de la question est simplement connecté à celui définissant la vue. L'ensemble constitue un arbre qui représente la question enrichie, qui est alors passée à l'optimiseur. La figure IX.3 illustre ce mécanisme pour la recherche des gros buveurs habitant à Versailles.

Dans cette section, nous examinons, d'un point de vue pratique puis théorique, le problème des mises à jour au travers des vues.

XIV-4-1. VUE METTABLE À JOUR▲

XIV-4-2. APPROCHE PRATIQUE▲

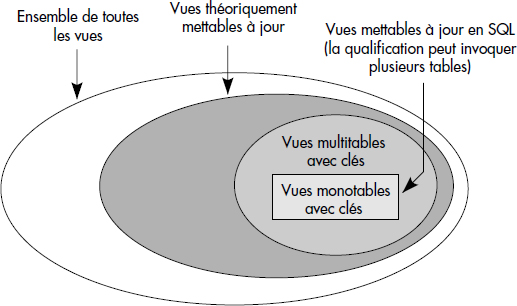
En pratique, la plupart des systèmes résolvent le problème en restreignant les possibilités de mise à jour à des vues monotables : seuls les attributs d'une table de la base doivent apparaître dans la vue. En imposant de plus que la clé de la table de la base soit présente, il est possible de définir une stratégie de mise à jour simple. Lors d'une insertion, on insère simplement les nouveaux tuples dont la clé n'existe pas, avec des valeurs nulles pour les attributs inexistants. Lors d'une suppression, on supprime les tuples répondant au critère. Lors d'une modification, on modifie les tuples répondant au critère. La définition de vue peut référencer d'autres tables qui permettent de préciser les tuples de la vue. En théorie, il faut vérifier que les tuples insérés, supprimés ou modifiés appartiennent bien à la vue. En pratique, SQL n'effectue cette vérification que si elle a été demandée lors de la définition de vue par la clause WITH CHECK OPTION.

Restreindre la mise à jour à des vues monotables est beaucoup trop fort. On peut simplement étendre, au moins en insertion et en suppression, aux vues multitables comportant les clés des tables participantes. Les attributs non documentés sont alors remplacés par des valeurs nulles lors des insertions. Cette solution pratique génère cependant des bases de données avec de nombreuses valeurs nulles. Elle sera souvent interdite dans les systèmes commercialisés. Ceux-ci sont donc loin de permettre toutes les mises à jour théoriquement possibles, comme le montre la figure IX.4.

XIV-4-3. APPROCHE THÉORIQUE▲

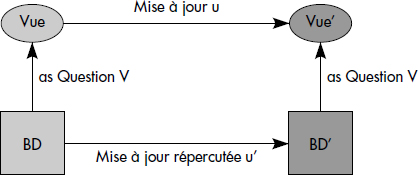
Le problème théorique est de définir une stratégie de report qui préserve la vue, quelle que soit la mise à jour : si l'on calcule la vue et on lui applique la mise à jour, on doit obtenir le même résultat que si on applique les mises à jour à la base et on calcule ensuite la vue. L'équation u(V(B)) = V(u'(B)) doit donc être vérifiée, en notant B la base, v le calcul de vue, u la mise à jour sur la vue et u' les mises à jour correspondantes sur la base. Autrement dit, le diagramme de la figure IX.5 doit commuter. D'autre part, il est évident qu'une bonne stratégie doit préserver le complément de la base, c'est-à-dire toutes les informations de la base qui ne figurent pas dans la vue [Bancilhon81]. Selon ces hypothèses raisonnables, le problème du calcul de u' n'a pas toujours une solution unique [Abiteboul91].

Une approche intéressante a été proposée récemment dans [Bentayeb97]. L'idée est de définir l'inverse de chaque opération relationnelle. En effet, soit V = E(R1, R2…Rn) une définition de vue. E est une expression de l'algèbre relationnelle. Si l'on peut définir l'inverse de chaque opération de l'algèbre sur une relation, on pourra alors calculer R1 × R2… × Rn = E^-1(V). La répercussion d'une mise à jour de V se fera simplement en unifiant Ri avec la projection de E^-1(V) sur Ri. Le problème de l'inversion de l'algèbre relationnelle a aussi été étudié dans [Imielinski83]. Désignons par t un tuple de la vue V et par [t] une table composée de ce seul tuple. L'image réciproque d'un tuple t par E peut être vue comme un ensemble de tables T1, T2…, Tn telles que E (T1, T2…, Tn) = [t]. Les tables Ti peuvent posséder des attributs inconnus désignés par des variables x, y, etc. Elles ne doivent pas contenir de tuples inutiles pour composer t, donc pour tout tuple ti ∈ Ti, E (T1…, Ti-[ti]…, Tn) ≠ [t]. Insérer le tuple t dans la vue V a alors pour effet de modifier les relations de base Ri en les unifiant avec les relations Ti. L'unification est une opération difficile, pas toujours possible, explicitée dans [Bentayeb97] sous forme d'algorithmes pour l'insertion et la suppression.

En résumé, la mise à jour au travers de vue est un problème complexe, bien étudié en théorie, mais dont les solutions pratiques sont réduites. Certains SGBD permettent des mises à jour de vues multitables en laissant l'administrateur définir la stratégie de report.

Dans cette section, nous abordons le problème des vues concrètes. Celles-ci sont particulièrement intéressantes dans les entrepôts de données (data warehouse), où elles facilitent l'analyse de données (OLAP) pour l'aide à la décision.

XIV-5-1. DÉFINITION▲

CREATE CONCRETE VIEW <SPÉCIFICATION DE VUE>.

VENTES(NUMV, NUMPRO, NUMFOU, DATE, QUANTITÉ, PRIX)

PRODUITS (NUMPRO, NOM, MARQUE, TYPE, PRIX)
FOURNISSEURS (NUMFOU, NOM, VILLE, RÉGION, TELEPHONE)

CREATE CONCRETE VIEW VENTESPFD(NUMPRO,NUMFOU,DATE,COMPTE,QUANTOT)AS
SELECT NUMPRO,NUMFOU,DATE,COUNT(*)AS COMPTE,SUM(QUANTITÉ) AS QUANTOT
FROM VENTES
GROUP BY NUMPRO, NUMFOU, DATE

CREATE CONCRETE VIEW VENTESPD (NUMPRO,DATE,COMPTE,QUANTOT) AS
SELECT NUMPRO, DATE,COUNT(*)AS COMPTE,SUM(QUANTITÉ) AS QUANTOT
FROM VENTES
GROUP BY NUMPRO, DATE

CREATE CONCRETE VIEW VENTESPD (NUMPRO, DATE, COMPTE,QUANTOT) AS
SELECT NUMPRO, DATE,SUM(COMPTE)AS COMPTE,SUM(QUANTOT) AS QUANTOT
FROM VENTESPFD
GROUP BY NUMFOU

CREATE CONCRETE VIEW VENTESPRD(NUMPRO,RÉGION,DATE,COMPTE,QUANTOT) AS
SELECT NUMPRO, DATE,COUNT(*)AS COMPTE,SUM(QUANTITÉ) AS QUANTOT
FROM VENTES V, FOURNISSEURS F
WHERE V.NUMFOU = F.NUMFOU
GROUP BY V.NUMPRO, F.RÉGION

XIV-5-2. STRATÉGIE DE REPORT▲

Les vues concrètes doivent être mises à jour lors de la mise à jour des relations de la base. Un problème important est de déterminer une stratégie de report efficace des mises à jour effectuées sur les relations de base. Bien sûr, il est possible de recalculer complètement la vue après chaque mise à jour, mais ceci est inefficace.

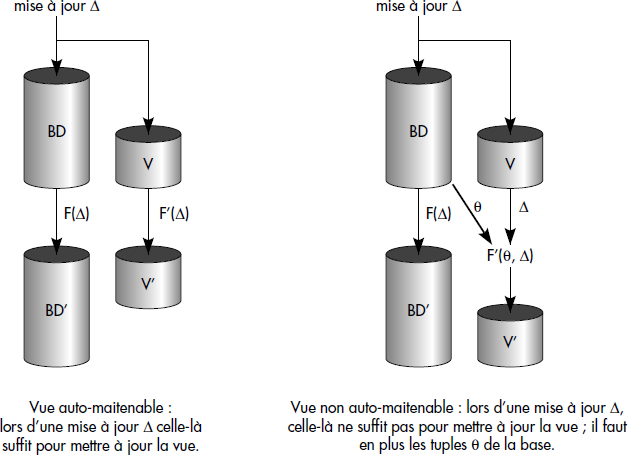
Une meilleure stratégie consiste à maintenir la vue concrète de manière différentielle, ou si l'on préfère incrémentale. Soit une vue V = F(R1, R2…Rn) définie sur les relations R1, R2… Rn. Des mises à jour sont effectuées par exemple sur la relation Ri. Soient des insertions de tuples notées Δ⁺Ri et des suppressions notées Δ^-Ri. Une modification de tuples existants peut toujours se ramener à une suppression suivie d'une insertion. L'effet net des mises à jour sur Ri est donc Ri = (Ri - Δ^-Ri) ∪ Δ⁺Ri. Le problème est de calculer l'effet net sur V, qui peut être exprimé par des tuples supprimés, puis par des tuples insérés comme suit : V = (V - Δ^-V) ∪ Δ⁺V. Dans certains cas, les mises à jour à apporter sur V (Δ^-V, Δ⁺V) peuvent être calculées à partir de celles apportées sur Ri (Δ^-Ri, Δ⁺Ri). La vue V est alors qualifiée d'automaintenable [Tompa88, Gupta95]

Notion IX.6 : Vue automaintenable (Self-maintenable view)

Vue concrète contenant suffisamment d'informations pour être mise à jour à partir des mises à jour des relations de base, sans accès aux tuples des relations de la base.

Cette notion est très importante dans les architectures distribuées (client-serveur, entrepôts de données, copies), où la vue est matérialisée sur un site différent de celui de la base. Elle est illustrée figure IX.6. Il est possible de distinguer l'automaintenabilité en insertion ou en suppression, c'est-à-dire lors des insertions ou suppressions dans une relation de base. L'automaintenabilité peut aussi être caractérisée pour chaque relation, et enfin généralisée au cas d'un groupe de vues [Huyn97].

En guise d'illustration, considérons la vue V1 des vins de Bordeaux définie ci-dessus comme une restriction de la table Vins : V1 = σ_{REGION = "Bordelais"} (VINS). Cette vue est automaintenable. En effet, comme la restriction commute avec la différence, il est simple de calculer :

• Δ+V1 = σ_{REGION = "Bordelais"} (Δ+VINS).
• Δ-V1 = σ_{REGION = "Bordelais"} (Δ-VINS).

Par suite, les mises à jour à apporter ΔV1 sont calculables sans accéder à la table VINS, mais seulement à partir des mises à jour de VINS. Malheureusement, dès qu'une vue comporte des projections avec élimination de doubles, des jointures ou des différences, elle n'est généralement plus automaintenable [Fabret94]. Par exemple, dans le cas de projections sans doubles, lorsque l'on enlève un tuple d'une table source, on ne sait plus s'il faut l'enlever de la vue, car sa projection peut provenir d'un autre tuple. De même, pour calculer le tuple à enlever dans une vue jointure lors d'une suppression d'un tuple dans une table, il faut accéder à l'autre table pour trouver les tuples jointures. De manière générale, savoir si une vue est automaintenable s'avère difficile, et même très difficile lorsque la vue contient des agrégats [Gupta96]. Ce dernier cas est examiné dans le paragraphe qui suit.

Dans le cas d'une vue calculée par sélections, projections et jointures (SPJ), les problèmes essentiels semblent provenir des jointures. Toute vue comportant toutes les informations de la base nécessaires à son calcul (attributs de projection et de jointure, tuples) est automaintenable en insertion ; en effet, la nouvelle instance de la vue V' est :

 

Sélectionnez

V' = F (R1…, Ri ∪ Δ+Ri…, Rn)

Comme F ne contient pas de différence, on a :

 

Sélectionnez

V' = F (R1…, Ri…, Rn) ∪ F (R1…, Δ+Ri…, Rn) = V ∪ F (R1…, Δ+Ri…, Rn)

d'où l'on déduit :

 

Sélectionnez

ΔV+ = F (R1…, Δ+Ri…, Rn)

Si F (R1…, Δ⁺Ri…, Rn) est calculable à partir de V et Δ⁺Ri, la vue est automaintenable en insertion. Tel est le cas à condition que V contienne les attributs et les tuples de R1…Rn nécessaires à son calcul. Les jointures externes seules ne perdent pas de tuples. Donc, une vue calculée par des jointures externes et projections est généralement automaintenable en insertion.

Pour l'automaintenabilité en suppression, le problème est plus difficile encore. On ne peut distribuer F par rapport à Ri - Δ^-Ri, ce qui rend le raisonnement précédent caduc. Cependant, toute vue contenant les attributs de R1…, Rn nécessaires à son calcul et au moins une clé de chaque relation de base est automaintenable. En effet, l'origine des tuples de la vue peut être identifiée exactement par les clés, ce qui permet de reporter les suppressions.

Des structures annexes associées à une vue peuvent aussi être maintenues [Colby96, Colby97]. Les reports sur la vue concrète peuvent être différés. La vue devient alors un cliché (snapshot) [Adiba80]. Beaucoup de SGBD supportent les clichés.

Notion IX.7 : Cliché (Snapshot)

Vue concrète d'une base de données mise à jour périodiquement.

La gestion de structures différentielles associées au cliché, par exemple les mises à jour sur chaque relation dont il est dérivé (les ΔRi), peut permettre un accès intégré à la vue concrète à jour et conduit au développement d'algorithmes de mise à jour spécialisés [Jagadish97].

XIV-5-3. LE CAS DES AGRÉGATS▲

AGG(v1,v2…vn) = AGG(AGG(v1…vi},AGG(vi+1..vn)).

CREATE CONCRETE VIEW VENTESPFD (NUMPRO,NUMFOU,DATE,COMPTE,QUANTOT)AS
SELECT NUMPRO,NUMFOU,COUNT(*)AS COMPTE,SUM(QUANTITÉ) AS QUANTOT
FROM VENTES
GROUP BY NUMPRO, NUMFOU

CREATE CONCRETE VIEW VENTESPFD (NUMPRO,NUMFOU,DATE,COMPTE,QUANTOT)AS
SELECT NUMPRO,NUMFOU,COUNT(*)AS COMPTE,MIN(QUANTITÉ) AS QUANMIN
FROM VENTES
GROUP BY NUMPRO, NUMFOU

La gestion de vues en interrogation est un problème bien compris dans les SGBD relationnels depuis la fin des années 70. Nous avons introduit ci-dessus ses principes de base. Le report des mises à jour des vues sur la base est un problème plus difficile encore. Des solutions pratiques et générales restent à inventer. L'utilisation de déclencheurs sur les vues peut être une solution pour définir les stratégies de report.

La matérialisation des vues a connu une nouvelle activité ces dernières années, avec l'apparition des entrepôts de données. Les vues avec agrégats sont particulièrement importantes pour gérer des données résumées, en particulier le fameux cube de données très utile en décisionnel. Les techniques sont maintenant connues. Il reste à les mettre en œuvre efficacement dans les systèmes, qui gèrent pour l'instant peu de redondances et souvent des organisations physiques ad hoc pour le multidimensionnel. Ceci n'est plus vrai dans les entrepôts de données, qui utilisent souvent les vues concrètes pour faciliter les calculs d'agrégats [Bello98].

Les vues connaissent aussi un nouveau développement dans le monde objet avec l'apparition de vues orientées objet au-dessus de bases de données relationnelles par exemple. Nous aborderons cet aspect dans le cadre des SGBD objet ou objet-relationnel.

[Abiteboul91] Abiteboul S., Hull R., Vianu V., Foundations of Databases, Addison-Wesley, 1995.

• Comme son nom l'indique, ce livre traite des fondements des bases de données relationnelles et objet. Souvent fondé sur une approche logique ou algébrique, il reprend toute la théorie des bases de données, y compris le problème de la mise à jour au travers des vues, parfaitement bien analysé.

[Adiba80] Adiba M., Lindsay B., « Database Snapshots », Intl. Conf. on Very Large Databases, IEEE Ed., Montréal, Canada, Sept. 1980.

• Cet article introduit la notion de cliché (snapshot) et montre son intérêt, notamment dans les bases de données réparties. Il décrit aussi la réalisation effectuée dans le fameux système R*.

[Adiba81] Adiba M., « Derived Relations : A Unified Mechanism for Views, Snapshots and Distributed Data », Intl. Conf. on Very Large Databases, IEEE Ed., Cannes, France, Sept. 1981.

• L'auteur généralise les clichés aux relations dérivées, dont il montre l'intérêt dans les bases de données réparties. Il discute aussi les algorithmes de mise à jour.

[Astrahan76] Astrahan M. M. et al., « System R : Relational Approach to Database Management », ACM TODS, V1, N2, Juin 1976.

• L'article de référence sur le fameux System R. Il décrit aussi le mécanisme de concaténation d'arbres implémenté pour la première fois dans ce système.

[Bancilhon81] Bancilhon F., Spyratos N., « Update Semantics and Relational Views », ACM TODS, V4, N6, Dec. 1981, p. 557-575.

• Un article de référence en matière de mises à jour de vues. Les auteurs posent le problème en termes d'invariance de la vue suite aux mises à jour directes ou répercutées dans la base. Ils montrent qu'une condition suffisante de maintenabilité est la possibilité de définir des stratégies de report à compléments constants.

[Bello98] Bello R.G, Dias K., Downing A., Freenan J., Norcott D., Dun H., Witkowski A., Ziauddin M., « Materialized Views in Oracle », Intl. Conf. on Very Large Databases, Morgan & Kauffman Ed., New York, USA, Août 1998, p. 659-664.

• Cet article explique la gestion des vues matérialisées dans Oracle 8. Celles-ci sont utilisées pour les entrepôts de données et la réplication. Elles peuvent être rafraîchies à la fin des transactions, sur demande ou périodiquement. Les rafraîchissements par lots sont optimisés. L'optimisation des requêtes prend en compte les vues concrètes à l'aide d'une technique de réécriture basée sur un modèle de coût.

[Bentayeb97] Bentayeb F., Laurent D., « Inversion de l'algèbre relationnelle et mises à jour », 13^e Journées Bases de Données Avancées (BDA 97), Ed. INRIA, Grenoble, 1997, p. 199-218.

• Cet article propose une approche déterministe de la mise à jour au travers de vue, fondée sur la notion d'image réciproque. Des algorithmes d'inversion de l'algèbre sont proposés. Une stratégie de report avec stockage éventuel dans la vue concrétisée est étudiée.

[Chamberlin75] Chamberlin D., Gray J., Traiger I., « Views, Authorization and Locking in a Relational Database System », Proc. National Computer Conf., 1975, p. 425-430.

• Cet article détaille les mécanismes de vue, d'autorisation et de verrouillage implantés dans System R.

[Colby96] Colby L.S., Griffin T., Libkin L., Mumick I., RTrickey H., « Algorithms for Deferred View Maintenance »,

• Int. Conf. on Management of Data, Montreal, USA, Mai 1996.

[Colby97] Colby L.S., Kawaguchi A., Lieuwen D.F, Mimick I.S., Ross K., « Supporting Multiple View Maintenance Policies », Proc. ACM SIGMOD Int. Conf. on Management of Data, Tucson, USA, p. 405-416, Mai 1997.

• Ces deux articles explorent différentes stratégies pour la maintenance de vues concrètes. Les auteurs proposent notamment des algorithmes qui garantissent la cohérence dans des cas de reports des mises à jour en temps différés, avec divers niveaux et groupes de vues.

[Dayal82] Dayal U., Bernstein P., « On the Correct Translation of Update Operations on Relational Views », ACM TODS, V8, N3, Dept. 1982.

• Cet article discute des stratégies de report de mise à jour au travers de vues et définit des critères de correction.

[Fabret94] Fabret F., Optimisation du calcul incrémental dans les langages de règles pour bases de données, Thèse, Université de Versailles SQ, Décembre 1994.

• Cette thèse présente une caractérisation des vues concrètes automaintenables dans les bases de données. Les vues sont définies par projection, jointure, union, différence et restriction. Cette thèse propose aussi des algorithmes afin de maintenir des réseaux de vues pour accélérer le calcul des requêtes dans une BD déductive.

[Gray96] Gray J., Bosworth A., Layman A., Pirahesh H., « Datacube : A relational Aggregation Operator Generalizing Group-by, Cross-tab, and Sub-totals », IEEE Int. Conf. on Data Engineering, p. 152-159, 1996.

• Cet article introduit un nouvel opérateur d'agrégation, appelé Datacube, afin de calculer des agrégats multidimensionnels. Nous étudierons plus en détail les opérateurs des bases de données multidimensionnelles dans le cadre du chapitre sur les entrepôts de données.

[Gupta95] Gupta M., Mumick I.S., « Maintenance of Materialized Views : Problems, Techniques and Applications », IEEE Data Engineering Bulletin, special Issue on Materialized Views and data Warehousing, N18(2), Juin 1995.

• Les auteurs introduisent les différents problèmes posés par la gestion de vues concrètes dans une base de données. Ils proposent quelques solutions et montrent quelques applications possibles pour la gestion d'entrepôts de données performants.

[Gupta96] Gupta A., Jagadish H.V., Mumick I.S., « Data Integration Using Self-Maintainable Views », Intl. Conf. on Extended Database Technology (EDBT), LCNS N1057, Avignon, France, 1996, p. 140-144.

• Cet article définit précisément la notion de vue automaintenable. Les auteurs établissent des conditions suffisantes pour qu'une vue selection-projection-jointure soit automaintenable.

[Huyn97] Huyn N., « Multiple-View Self-Maintenance in Data Warehousing Environments » Intl. Conf. on Very Large Databases, Morgan & Kauffman Ed., Athens, Grèce, Août 1997, p. 26-35.

• Cet article étudie le problème de l'automaintenabilité d'un ensemble de vues. Il propose des algorithmes qui permettent de tester si un groupe de vues est automaintenable par génération de requêtes SQL. De plus, dans le cas où la réponse est positive, les algorithmes génèrent les programmes de mises à jour.

[Jagadish97] Jagadish H.V., Narayan P.P.S., Seshadri S., Sudarshan S., Kanneganti R., « Incremental Organization for Data Recording and Warehousing », Intl. Conf. on Very Large Databases, Morgan & Kauffman Ed., Athens, Greece, Août 1997, p. 16-25.

• Les auteurs proposent deux techniques, la première basée sur des séquences triées insérées dans un B-tree, la seconde sur une organisation par hachage, pour stocker les enregistrements lors de leur arrivée dans un entrepôt de données, avant leur intégration dans les vues matérialisées. Ces techniques précisément évaluées supportent des environnements concurrents avec reprises.

[Keller87] Keller M.A., « Comments on Bancilhon and Spyratos's Update Semantics and Relational Views », ACM TODS, V12, N3, Sept. 1987, p. 521-523.

• Cet article montre que la condition suffisante de maintenabilité qu'est la possibilité de définir des stratégies de report à compléments constants est trop forte, et qu'elle peut conduire à interdire des stratégies intéressantes.

[Kerhervé86] Kerhervé B., « Vues Relationnelles : Implémentation dans un SGBD centralisé et distribué », Thèse de doctorat, Université de Paris VI, Mars 1986.

• Cette thèse décrit l'implémentation de vues réalisée dans le SGBD SABRE à l'INRIA. Un mécanisme de gestion de vues concrètes par manipulation de compteurs au niveau des opérateurs relationnels est aussi proposé.

[Nicolas83] Nicolas J-M., Yazdanian K., « An Outline of BDGen : A Deductive DBMS », Woldwide IFIP Congress, Paris, 1983.

• Cet article introduit le système déductif BDGen réalisé au CERT à Toulouse. Il maintient des vues définies par des règles en utilisant des compteurs de raisons de présence d'un tuple.

[Stonebraker74] Stonebraker M.R., « A Functional View of Data Independance », ACM SIGMOD Workshop on Data Description, Access and Control, ACM Ed., mai 1974.

• Un des premiers articles de Mike Stonebraker, l'un des pères du système INGRES. Il plaide ici pour l'introduction de vues assurant l'indépendance logique.

[Stonebraker75] Stonebraker M., « Implémentation of Integrity Constraints and Views by Query Modification », Proc. ACM-SIGMOD Intl. Conf. On Management of data, San José, CA 1975.

• Cet article propose de modifier les questions au niveau du code source par la définition de vues pour répondre aux requêtes. La technique est formalisée avec le langage QUEL d'INGRES, où elle a été implémentée.