XV. OPTIMISATION DE QUESTIONS▲
XV-1. INTRODUCTION▲
La plupart des SGBD relationnels offrent aujourd'hui des langages de manipulation basés sur SQL, non procéduraux et utilisant des opérateurs ensemblistes. Avec de tels langages, l'utilisateur définit les données qu'il veut visualiser sans fournir les algorithmes d'accès aux données. Le but des algorithmes d'optimisation de questions est justement de déterminer les algorithmes d'accès. Ces algorithmes sont aussi utiles pour les mises à jour, car une mise à jour est une question suivie d'un remplacement. Plus précisément, il s'agit d'élaborer un programme d'accès composé d'opérations de bas niveau attachées à des algorithmes efficaces de recherche dans les tables. Il est essentiel pour un système de déterminer des plans d'accès optimisés - ou au moins proches de l'optimum - pour les questions les plus fréquentes. Ce n'est pas là un problème facile, comme nous allons le voir dans ce chapitre.
Depuis 1975, l'optimisation de requêtes dans les bases de données relationnelles a reçu une attention considérable [Jarke84, Kim85, Graefe93]. Les systèmes ont beaucoup progressé. Alors que les premiers étaient très lents, capables seulement d'exécuter quelques requêtes par seconde sur les bases de données du benchmark TPC/A ou B [Gray91], ils supportent aujourd'hui des milliers de transactions par seconde. Bien sûr, cela n'est pas dû seulement à l'optimiseur, mais aussi aux progrès du matériel (les temps d'entrée-sortie disque restent cependant de l'ordre de la dizaine de millisecondes) et des méthodes d'accès. L'optimiseur est donc un des composants essentiels du SGBD relationnel ; avec les nouveaux SGBD objet-relationnel ou objet, il devient encore plus complexe. Dans ce chapitre, nous nous consacrons au cas relationnel. Nous étudierons plus loin dans cet ouvrage le cas des nouveaux SGBD, où l'optimiseur doit être extensible, c'est-à-dire capable de supporter des opérateurs non prévus au départ.
Classiquement, un optimiseur transforme une requête exprimée dans un langage source (SQL) en un plan d'exécution composé d'une séquence d'opérations de bas niveau réalisant efficacement l'accès aux données. Le langage cible est donc constitué d'opérateurs de bas niveau, souvent dérivés de l'algèbre relationnelle complétée par des informations de niveau physique, permettant de déterminer l'algorithme choisi pour exécuter les opérateurs [Selinger79]. Ces informations associées à chaque opérateur, appelées annotations, dépendent bien sûr du schéma interne de la base (par exemple de l'existence d'un index) et de la taille des tables. Elles complètent utilement l'algèbre pour choisir les meilleurs chemins d'accès aux données recherchées.
Au-delà de l'analyse de la question, l'optimisation de requêtes est souvent divisée en deux phases : l'optimisation logique, qui permet de réécrire la requête sous une forme canonique simplifiée et logiquement optimisée, c'est-à-dire sans prendre en compte les coûts d'accès aux données, et l'optimisation physique, qui effectue le choix des meilleurs algorithmes pour les opérateurs de bas niveau compte tenu de la taille des données et des chemins d'accès disponibles. L'optimisation logique reste au niveau de l'algèbre relationnelle, alors que l'optimisation physique permet en particulier d'élaborer les annotations. Les optimisations logique et physique ne sont malheureusement pas indépendantes ; les deux peuvent en effet changer l'ordre des opérateurs dans le plan d'exécution et modifier le coût du meilleur plan retenu.
Ce chapitre présente d'abord plus précisément les objectifs de l'optimisation et introduit les éléments de base. La section 3 est consacrée à l'étude des principales méthodes d'optimisation logique ; celles-ci recherchent en général la question la plus simple équivalente à la question posée et utilisent une heuristique de restructuration algébrique pour élaborer une forme canonique. Nous abordons ensuite l'étude des différents algorithmes d'accès physique aux données : sélection, tri, jointure et calcul d'agrégats. Les variantes sans index et avec index des algorithmes sont discutées. Pour chaque algorithme, un coût approché est calculé en nombre d'entrées-sorties. En effet, l'optimisation physique nécessite un modèle de coût pour estimer le coût de chaque plan d'exécution afin de choisir le meilleur, ou au moins un proche du meilleur. Un modèle de coût complet est décrit au paragraphe 5. Enfin, le paragraphe 6 résume les stratégies essentielles permettant de retrouver un plan d'exécution proche de l'optimal. En conclusion, nous discutons des problèmes plus avancés en matière d'optimisation relationnelle, liés au parallélisme et à la répartition des données.
XV-2. LES OBJECTIFS DE L'OPTIMISATION▲
Cette section propose deux exemples de bases de données, situe les objectifs de l'optimisation, et définit les concepts de base essentiels.
XV-2-1. EXEMPLES DE BASES ET REQUÊTES▲
À titre d'illustration, nous utiliserons une extension de notre base favorite des buveurs, composée de cinq relations :
BUVEURS (NB, NOM, PRÉNOM, TYPE)
VINS (NV, CRU, MILLESIME, DEGRÉ)
ABUS (NB, NV, DATE, QUANTITÉ)
PRODUCTEURS (NP, NOM, REGION)
PRODUIT (NV, NP)Les tables BUVEURS, VINS et PRODUCTEURS correspondent à des entités alors que ABUS et PRODUIT sont des tables représentant des associations. La table BUVEURS décrit des buveurs caractérisés par un numéro, un nom et un prénom. La table VINS contient des vins caractérisés par un numéro, un cru, un millésime et un degré. Les abus commis par les buveurs associant un numéro de buveur, un numéro de vin bu, une date et une quantité bue, sont enregistrés dans la table ABUS. La table PRODUCTEURS décrit des producteurs caractérisés par un numéro, un nom et une région. L'association entre un vin et le producteur qui l'a produit est mémorisée dans la table PRODUIT. On considérera par exemple la question « Quels sont les crus des vins produits par un producteur bordelais en 1976 ayant un degré inférieur ou égal à 14 ? ». Celle-ci s'écrit comme suit en SQL :
SELECT V.CRU
FROM PRODUCTEURS P, VINS V, PRODUIT R
WHERE V.MILLESIME = "1976" AND V.DEGRE ≤ 14
AND P.REGION = "BORDELAIS" AND P.NP = R.NP
AND R.NV = V.NVPour diversifier un peu les exemples, nous considérerons aussi parfois la base de données dérivée du banc d'essai (benchmark) TPC-D [TPC95]. Ce banc d'essai est centré sur l'aide à la décision et comporte donc beaucoup de questions avec des agrégats sur une base plutôt complexe. C'est dans de telles conditions que l'optimisation de questions devient une fonction très importante. Le schéma simplifié de la base est le suivant :
COMMANDES(NUMCO, NUMCLI, ETAT, PRIX, DATE, PRIORITÉ, RESPONSABLE, COMMENTAIRE)
LIGNES(NUMCO, NUMLIGNE, NUMPRO, FOURNISSEUR, QUANTITÉ, PRIX, REMISE,
TAXE, ÉTAT, DATELIVRAISON, MODELIVRAISON, INSTRUCTIONS, COMMENTAIRE)
PRODUITS(NUMPRO, NOM, FABRIQUANT, MARQUE, TYPE, FORME, CONTAINER, PRIX, COMMENTAIRE)
FOURNISSEURS(NUMFOU, NOM, ADRESSE, NUMPAYS, TELEPHONE, COMMENTAIRE)
PRODFOURN(NUMPRO, NUMFOU, DISPONIBLE, COUTLIVRAISON, COMMENTAIRE)
CLIENTS(NUMCLI, NOM, ADRESSE, NUMPAYS, TELEPHONE, SEGMENT, COMMENTAIRE)
PAYS(NUMPAYS, NOM, NUMCONT, COMMENTAIRE)
CONTINENTS(NUMCONT, NOM, COMMENTAIRE)Cette base décrit des commandes composées d'un numéro absolu, d'un numéro de client ayant passé la commande, d'un état, d'un prix, d'une date, d'une priorité, d'un nom de responsable et d'un commentaire textuel de taille variable. Chaque ligne de commande est décrite par un tuple dans la table LIGNES. Celle-ci contient le numéro de la commande référencée, le numéro de la ligne et le numéro de produit qui référence un produit de la table PRODUITS. Les fournisseurs et les clients sont décrits par les attributs indiqués dont la signification est évidente, à l'exception de l'attribut SEGMENT qui précise le type de client. La table associative PROFOURN relie chaque fournisseur aux produits qu'il est capable de fournir ; elle contient pour chaque couple possible la quantité disponible, le coût de la livraison par unité et un commentaire libre. Les tables PAYS et CONTINENTS sont liées entre elles par le numéro de continent ; elles permettent de connaître les pays des fournisseurs et des clients, ainsi que le continent d'appartenance de chaque pays.
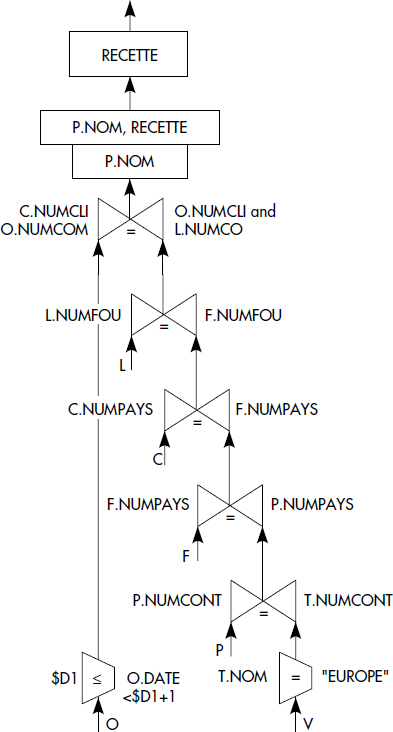
La question suivante est une requête décisionnelle extraite de la vingtaine de requêtes du banc d'essai. Elle calcule les recettes réalisées par des ventes de fournisseurs à des clients appartenant au même pays, c'est-à-dire les recettes résultant de ventes internes à un pays, et ceci pour tous les pays d'Europe pendant une année commençant à la date D1.
SELECT P.NOM, SUM(L.PRIX * (1-L.REMISE* QUANTITÉ) AS RECETTE
FROM CLIENTS C, COMMANDES O, LIGNES L, FOURNISSEURS F, PAYS P, CONTINENTS T
WHERE C.NUMCLI = O.NUMCLI
AND O.NUMCOM = L.NUMCO
AND L.NUMFOU = F.NUMFOU
AND C.NUMPAYS = F.NUMPAYS
AND F.NUMPAYS = P.NUMPAYS
AND P.NUMCONT = T.NUMCONT
AND T.NOM = "EUROPE"
AND O.DATE ≥ $D1
AND O.DATE < $D1 + INTERVAL 1 YEAR
GROUP BY P.NOM
ORDER BY P.NOM, RECETTE DESC;Il s'agit là d'une requête complexe contenant six jointures, trois restrictions dont deux paramétrées par une date ($D1), un agrégat et un tri ! De telles requêtes sont courantes dans les environnements décisionnels.
XV-2-2. REQUÊTES STATIQUES OU DYNAMIQUES▲
Certaines requêtes sont figées lors de la phase de développement et imbriquées dans des programmes d'application, donc exécutées aussi souvent que le programme qui les contient. D'autres au contraire sont construites dynamiquement, par exemple saisies une seule fois pour un test ou une recherche ad hoc. Pour l'optimiseur, il est important de distinguer ces différents types de requêtes. Les premières répétitives sont appelées requêtes statiques, alors que les secondes sont qualifiées de requêtes dynamiques.
Notion X.1 : Requête statique (Static Query)
Requête SQL généralement intégrée à un programme d'application dont le code SQL est connu à l'avance et fixé, souvent exécutée plusieurs fois.
Ce premier type de requête gagne à être optimisé. En effet, l'optimisation est effectuée une seule fois, lors de la compilation du programme contenant la requête, pour des milliers, voire des millions d'exécutions. La requête SQL peut être paramétrée, les valeurs constantes étant passées par des variables de programme. L'optimiseur doit donc être capable d'optimiser des requêtes paramétrées, par exemple contenant un prédicat CRU = $x, ou x est une variable de programme.
Notion X.2 : Requête dynamique (Dynamic Query)
Requête SQL généralement composée en interactif dont le code n'est pas connu à l'avance, souvent exécutée une seule fois.
Ce deuxième type de requêtes, aussi appelées requêtes ad hoc, car correspondant à des requêtes souvent saisies en ligne sans une longue réflexion préalable, est exécuté une seule fois. On doit donc limiter le temps d'optimisation afin de ne pas trop pénaliser l'unique exécution de la requête.
XV-2-3. ANALYSE DES REQUÊTES▲
Dans un premier temps, une question est analysée du point de vue syntaxique. L'existence des noms de relations et d'attributs cités est vérifiée par rapport au schéma. La correction de la qualification de la question est analysée. Aussi, la requête est mise dans une forme canonique. Par exemple, celle-ci peut être mise en forme normale conjonctive (ET de OU) ou disjonctive (OU de ET), selon qu'elle sera ultérieurement traitée par des opérateurs élémentaires supportant le OU (forme normale conjonctive), ou simplement comme plusieurs questions (forme normale disjonctive). Souvent, cette transformation est accomplie au niveau suivant. Finalement, ce premier traitement est analogue à l'analyse syntaxique d'expressions dans un langage de programmation.
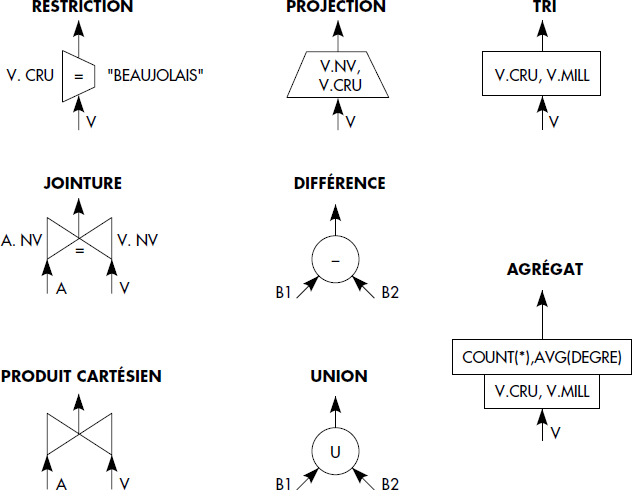
À partir de la requête analysée, la plupart des systèmes génèrent un arbre d'opérations de l'algèbre relationnelle (projection, restriction, jointure, union, différence, intersection), éventuellement étendu avec des agrégats et des tris, appelé arbre algébrique, ou arbre relationnel, ou parfois aussi arbre de traitement (processing tree).
Notion X.3 : Arbre algébrique (Algebraic tree)
Arbre représentant une question dont les nœuds terminaux représentent les relations, les nœuds intermédiaires des opérations de l'algèbre relationnelle, le nœud racine le résultat d'une question et les arcs les flux de données entre les opérations.
Dans l'arbre algébrique, chaque nœud est représenté par un graphisme particulier, déjà décrit lors de l'introduction des opérateurs algébriques. Nous rappelons les notations figure X.1, en introduisant une notation particulière pour les tris (simplement un rectangle avec le nom des attributs de tri à l'intérieur) et les agrégats, qui peuvent être vus comme un tri suivi d'un groupement avec calculs de fonctions pour chaque monotonie. Les agrégats sont ainsi représentés par un rectangle contenant les attributs de la clause GROUP BY, suivi d'un rectangle contenant les attributs résultats calculés.
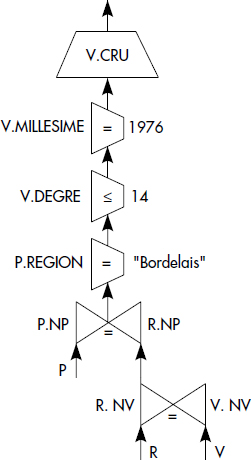
Plusieurs arbres représentent une même question, selon l'ordre choisi pour les opérations. Une méthode de génération simple d'un arbre consiste à prendre les prédicats de qualification dans l'ordre où ils apparaissent et à leur associer l'opération relationnelle correspondante, puis à ajouter les agrégats, et enfin une projection finale pour obtenir le résultat avec un tri éventuel. Cette méthode permet par exemple de générer l'arbre représenté figure X.2 pour la question Q1, puis l'arbre de la figure X.3 pour la question Q2.
À partir d'un arbre algébrique, il est possible de générer un plan d'exécution en parcourant l'arbre, des feuilles vers la racine. Une opération peut être exécutée par ensembles de tuples ou tuple à tuple, dès que ses opérandes sont disponibles. L'exécution ensembliste consiste à attendre la disponibilité des opérandes pour exécuter une opération.
Notion X.4 : Exécution ensembliste (Set-oriented Execution)
Mode d'exécution consistant à calculer l'ensemble des tuples des relations en entrée d'un opérateur avant d'évaluer cet opérateur.
Dans ce mode, si l'opération O1 n'utilise pas les résultats de l'opération O2, les opérations O1 et O2 peuvent être exécutées en parallèle. Ce mode d'exécution peut être intéressant pour des algorithmes capables de travailler efficacement sur des ensembles (basés sur le tri par exemple).
Plus souvent, on cherche à démarrer une opération dès qu'un tuple est disponible dans l'une des tables arguments. C'est le mode tuple à tuple ou pipeline.
Notion X.5 : Exécution pipeline (Pipeline execution)
Mode d'exécution consistant à démarrer une opération le plus tôt possible, si possible dès qu'un tuple est disponible pour au moins un opérande.
Pour les opérations unaires, il suffit qu'un tuple soit disponible. On peut ainsi exécuter deux opérations successives de restriction en pipeline, c'est-à-dire commencer la deuxième dès qu'un tuple (ou un groupe de tuples, par exemple une page) a été généré par la première. Les opérations binaires comme la différence peuvent nécessiter d'avoir à calculer complètement l'un des deux opérandes pour commencer. Le mode pipeline est donc seulement possible sur un des deux opérandes. Ceci peut dépendre de l'algorithme pour la jointure.
XV-2-4. FONCTIONS D'UN OPTIMISEUR▲
Un optimiseur a donc pour objectif d'élaborer un plan d'exécution optimisé.
Notion X.6 : Plan d'exécution (Execution plan)
Programme éventuellement parallèle d'opérations élémentaires à exécuter pour évaluer la réponse à une requête.
Ceci s'effectue en général en deux phases, la réécriture et le planning, encore appelé ordonnancement [Haas89].
Notion X.7 : Réécriture (Rewriting)
Phase d'optimisation consistant à transformer logiquement la requête de sorte à obtenir une représentation canonique.
Cette phase comporte un aspect sémantique pouvant aller jusqu'à prendre en compte des règles d'intégrité, et un aspect syntaxique concernant le choix d'une forme canonique. Celle-ci comprend la mise sous forme normale des critères et l'affectation d'un ordre fixé pour les opérateurs algébriques.
La phase suivante est donc le planning, qui peut remettre en question certains choix effectués lors de la réécriture.
Notion X.8 : Planning (Planning)
Phase d'optimisation consistant à ordonner les opérateurs algébriques et choisir les algorithmes et modes d'exécution.
Alors que la première phase génère un arbre logique, la seconde ajoute les annotations et obtient un plan d'exécution. Elle s'appuie de préférence sur un modèle de coût. Les deux phases ne sont pas indépendantes, la première pouvant influer sur la seconde et biaiser le choix du meilleur plan. Cependant, on les distingue souvent pour simplifier.
On cherche bien sûr à optimiser les temps de réponse, c'est-à-dire à minimiser le temps nécessaire à l'exécution d'un arbre. Le problème est donc de générer un arbre optimal et de choisir les meilleurs algorithmes pour exécuter chaque opérateur et l'arbre dans son ensemble. Pour cela, il faut optimiser simultanément :
- le nombre d'entrées-sorties ;
- le parallélisme entre les opérations ;
- le temps de calcul nécessaire.
La fonction de coût doit si possible prendre en compte la taille des caches mémoires disponibles pour l'exécution. L'optimisation effectuée dépend en particulier de l'ordre des opérations apparaissant dans l'arbre algébrique utilisé et des algorithmes retenus. Il est donc essentiel d'établir des règles permettant de générer, à partir d'un arbre initial, tous les plans possibles afin de pouvoir ensuite choisir celui conduisant au coût minimal. En fait, le nombre d'arbres étant très grand, on est amené à définir des heuristiques pour déterminer un arbre proche de l'optimum.
Nous allons maintenant étudier les principales méthodes proposées pour accomplir tout d'abord la réécriture, puis le planning. Leur objectif essentiel est évidemment d'optimiser les temps de réponse aux requêtes.
XV-3. L'OPTIMISATION LOGIQUE OU RÉÉCRITURE▲
La réécriture permet d'obtenir une représentation canonique de la requête, sous la forme d'un arbre algébrique dans lequel les opérations sont ordonnées et les critères mis sous forme normale. Elle peut comporter elle-même deux étapes : la réécriture sémantique qui transforme la question en prenant en compte les connaissances sémantiques sur les données (par exemple, les contraintes d'intégrité), et la réécriture syntaxique qui profite des propriétés simples de l'algèbre relationnelle pour ordonner les opérations.
XV-3-1. ANALYSE ET RÉÉCRITURE SÉMANTIQUE▲
Ce type d'analyse a plusieurs objectifs, tels que la détermination de la correction de la question, la recherche de questions équivalentes par manipulation de la qualification ou à l'aide des contraintes d'intégrité. Ce dernier type d'optimisation est d'ailleurs rarement réalisé dans les systèmes. On peut aussi inclure dans la réécriture les modifications de questions nécessaires pour prendre en compte les vues, problème étudié dans le chapitre traitant des vues.
XV-3-1-1. Graphes support de l'analyse▲
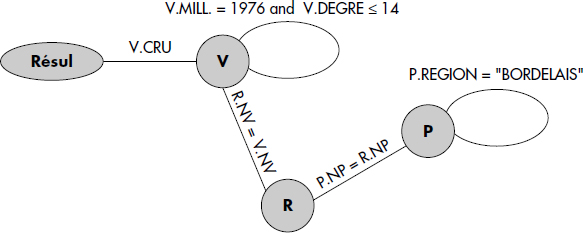
Plusieurs types de graphes sont utilisés pour effectuer l'analyse sémantique d'une question. Tout d'abord, le graphe de connexion des relations a été introduit dans INGRES [Wong76].
Notion X.9 : Graphe de connexion des relations (Relation connection graph)
Graphe dans lequel : (a) un sommet est associé à chaque occurrence de relation, (b) une jointure est représentée par un arc entre les deux nœuds représentant les relations jointes, (c) une restriction est représentée par une boucle sur la relation à laquelle elle s'applique, (d) la projection finale est représentée par un arc d'un nœud relation vers un nœud singulier résultat.
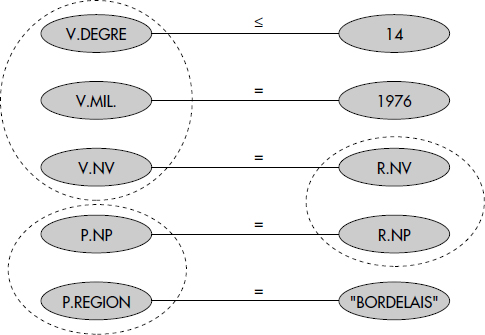
Avec SQL, chaque instance de relation dans la clause FROM correspond à un nœud. Les arcs sont valués par la condition qu'ils représentent. Ainsi, le graphe de connexion des relations de la question Q1 est représenté figure X.4. Notez la difficulté à représenter des questions avec des disjonctions (ou) de jointures qui peuvent être modélisées par plusieurs graphes.
Plusieurs variantes d'un tel graphe ont été proposées, en particulier le graphe des jointures [Berstein79] où seules les jointures sont matérialisées par un arc entre les nœuds relations. Le nœud singulier figurant le résultat, les arcs représentant les projections finales et les boucles symbolisant les restrictions sont omis. Ce graphe simplifié peut être utilisé pour diverses manipulations sémantiques sur les jointures, mais aussi pour ordonner les jointures ; il est alors couplé à un modèle de coût.
Le graphe de connexion des attributs peut être défini comme suit [Hevner79].
Notion X.10 : Graphe de connexion des attributs (Attribute connection graph)
Graphe dans lequel : (a) un sommet est associé à chaque référence d'attribut ou de constante, (b) une jointure est représentée par un arc entre les attributs participants, (c) une restriction est représentée par un arc entre un attribut et une constante.
La figure X.5 représente le graphe de connexion des attributs de la question Q1. Notez que ce graphe perd la notion de tuple, chaque attribut étant représenté individuellement.
Il est possible d'introduire des hypernœuds (c'est-à-dire des groupes de nœuds) pour visualiser les attributs appartenant à un même tuple, comme représentés figure X.5. Un tel graphe permet de découvrir les critères contenant une contradiction : il possède alors un cycle qui ne peut pas être satisfait par des constantes. Il peut aussi permettre de découvrir des questions équivalentes à la question posée par transitivité (voir ci-dessous).
XV-3-1-2. Correction de la question▲
La notion de question correcte est à préciser. Deux catégories d'incorrections sont à distinguer :
- Une question peut être mal formulée, car certaines parties apparaissent inutiles dans la question ; c'est sans doute que l'utilisateur a oublié une jointure dans la question.
- Une question peut présenter une qualification contradictoire, qui ne peut être satisfaite par aucun tuple, par exemple la question « crus des vins de degré supérieur à 14 et inférieur à 12 ».
Deux résultats importants ont été établis afin d'éliminer les questions incorrectes, dans le cas des questions conjonctives (sans ou) avec des opérateurs de comparaisons =, <, >, ≤, ≥ :
- Une question est généralement mal formulée si son graphe de connexion des relations n'est pas connexe [Wong76]. En effet, tout sous-graphe non relié au nœud résultat ne participe pas à ce résultat. Il peut cependant s'agir d'un filtre qui rend la réponse vide si aucun tuple de la base ne le satisfait.
- Une question est contradictoire si son graphe de connexion des attributs complété par des arcs de comparaison entre constantes présente un cycle non satisfaisable [Rosenkrantz80]. En effet, dans ce cas, aucun tuple ne peut satisfaire les prédicats du cycle, par exemple du style AGE < 40 et AGE >50.
XV-3-1-3. Questions équivalentes par transitivité▲
La notion de questions équivalentes mérite une définition plus précise [Aho79].
Notion X.11 : Questions équivalentes (Equivalent queries)
Deux questions sont équivalentes si et seulement si elles donnent le même résultat pour toute extension possible de la base de données.
Ainsi, quels que soient les tuples dans la base (obéissant évidemment aux contraintes d'intégrité), deux questions équivalentes exécutées au même instant donneront le même résultat.
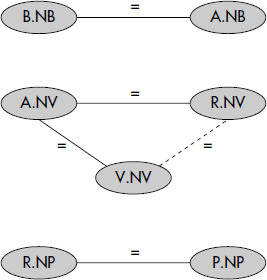
Tout d'abord, des questions équivalentes peuvent être générées par l'étude des propriétés de transitivité du graphe de connexion des attributs. Si l'on considère ce dernier, tout couple d'attributs (x, y) reliés par un chemin x -> y dont les arcs sont étiquetés par des égalités doit vérifier x = y. Il est alors possible de générer la fermeture transitive de ce graphe. Tous les sous-graphes ayant même fermeture transitive génèrent des questions équivalentes, bien qu'exprimées différemment. Ils correspondent en effet à des contraintes équivalentes sur le contenu de la base. Par exemple, considérons la question Q3 : « Noms des buveurs ayant bu un Bordeaux de degré supérieur ou égal à 14 ». Elle peut s'exprimer comme suit :
SELECT B.NOM
FROM BUVEURS B, ABUS A, PRODUIT R, PRODUCTEURS P, VINS V
WHERE B.NB = A.NB AND A.NV = R.NV AND R.NV = V.NV
AND R.NP = P.NP AND P.REGION = "BORDELAIS"
AND V.DEGRE ≥ 14 ;où B, A, R, P, V désignent respectivement les relations BUVEURS, ABUS, PRODUIT, PRODUCTEURS et VINS. Le graphe de connexion des attributs réduit aux jointures de Q3 est représenté figure X.6. Sa fermeture transitive apparaît en pointillés. Un graphe ayant même fermeture transitive est représenté figure X.7figure X.7. Ainsi la question Q3 peut être posée par la formulation résultant du graphe de la avec les mêmes variables, comme suit :
SELECT B.NOM
FROM BUVEURS B, ABUS A, PRODUIT R, PRODUCTEURS P, VINS V
WHERE B.NB = A.NB AND A.NV = R.NV AND A.NV = V.NV
AND R.NP = P.NP AND P.REGION = "BORDELAIS"
AND V.DEGRE ≥ 14 ;La différence réside dans le choix des jointures, le prédicat R.NV = V.NV étant remplacé par A.NV = V.NV. D'autres expressions sont possibles. Le problème consiste bien sûr à choisir celle qui pourra être évaluée le plus rapidement. Le problème est plus difficile si l'on considère des inégalités, mais il peut être résolu en étendant le graphe de connexion des attributs [Rosenkrantz80].
XV-3-1-4. Questions équivalentes par intégrité▲
Une autre manière de générer des questions équivalentes consiste à utiliser les contraintes d'intégrité [Chakravarthy90, King81, Finance94]. Le problème peut être posé comme suit. Étant donnés une question de qualification Q et un ensemble de contraintes d'intégrité I1, I2 … In, si Q est contradictoire à une contrainte, la question a une réponse vide. Sinon, il suffit d'évaluer la « meilleure » qualification Q' impliquant Q sous les contraintes I1, I2… In, c'est-à-dire telle que I1 ∧ I2 ∧ …In ∧ Q' ⇒ Q.
Le problème est un problème de déduction que nous illustrerons simplement par un exemple. Soit la contrainte exprimant que tous les Bordeaux sont de degré supérieur à 15 (où P désigne un tuple de PRODUCTEURS, R un tuple de PRODUIT et V désigne un tuple de VINS) :
P.REGION = "BORDELAIS"
AND P.NP = R.NP AND R.NV = V.NV AND V.DEGRE > 15Alors, la qualification de la question Q1 est contradictoire avec cette contrainte et par conséquent sa réponse est vide. En revanche, cette contrainte permet de simplifier la question Q3, car la condition V.DEGRE ≥ 14 est inutile et peut donc être supprimée. Il n'est pas sûr que cette simplification réduise le temps d'exécution.
L'optimisation sémantique a été particulièrement développée dernièrement dans le contexte des bases de données objet, où elle peut conduire à des optimisations importantes. Les contraintes d'équivalence, d'implication, d'unicité de clé et d'inclusion sont particulièrement utiles pour transformer et simplifier les requêtes.
XV-3-2. RÉÉCRITURES SYNTAXIQUES ET RESTRUCTURATIONS ALGÉBRIQUES▲
Nous introduisons ici une technique de base pour transformer les arbres algébriques et changer l'ordre des opérations. Cette technique résulte des propriétés de commutativité et d'associativité des opérateurs de l'algèbre. Elle provient d'une traduction dans le contexte de l'algèbre relationnelle des techniques de réécriture des expressions arithmétiques. Aujourd'hui, la plupart des optimiseurs mixent les restructurations algébriques avec la phase de planning, basée sur un modèle de coût, que nous décrivons plus loin. Cependant, pour la commodité de la présentation, nous introduisons ci-dessous les règles de transformation des arbres, puis un algorithme simple de restructuration algébrique, et aussi des heuristiques plus complexes de décomposition appliquées parfois par certains optimiseurs [Stonebraker76, Gardarin84].
XV-3-2-1. Règles de transformation des arbres▲
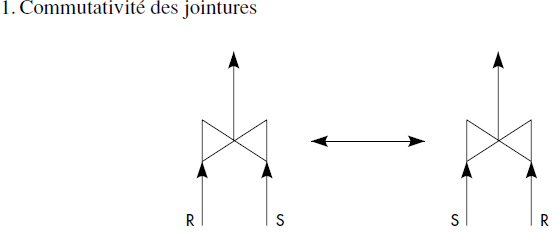
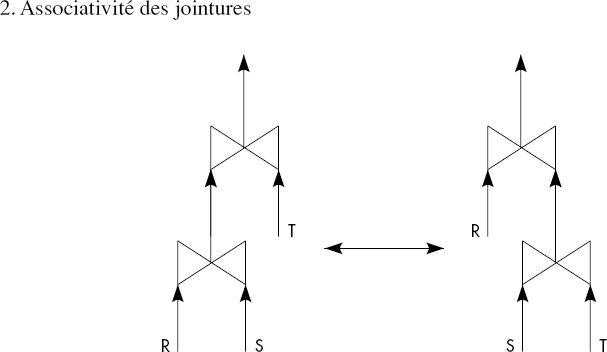
Les règles suivantes ont pour la première fois été précisées dans [Smith75]. Elles sont bien développées dans [Ullman88]. Elles dépendent évidemment des opérations relationnelles prises en compte. Nous considérons ici l'ensemble des opérations de restriction, jointure, union, intersection et différence. Nous représentons figure X.8 neuf règles sous forme de figures donnant deux patrons d'arbres équivalents. Ces règles sont très classiques. Ce sont les suivantes :
- Commutativité des jointures ;
- Associativité des jointures ;
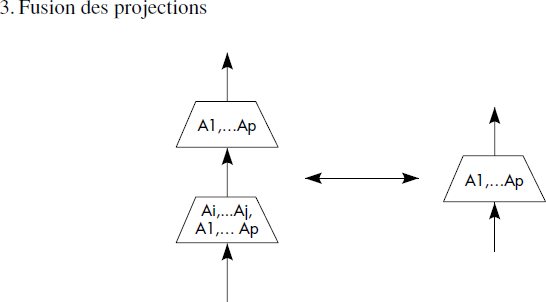
- Fusion des projections ;
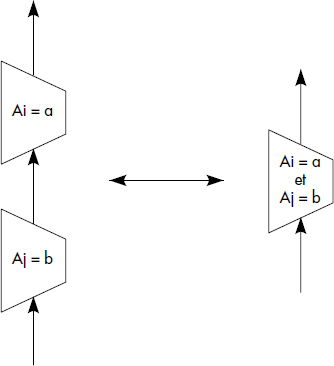
- Regroupement des restrictions ;
- Quasi-commutativité des restrictions et des projections ;
- Quasi-commutativité des restrictions et des jointures ;
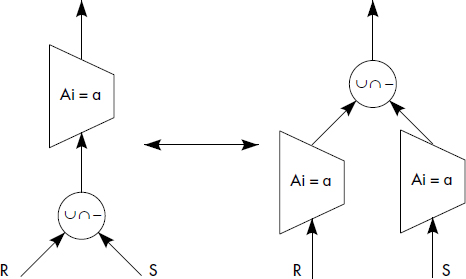
- Commutativité des restrictions avec les unions, intersections ou différences ;
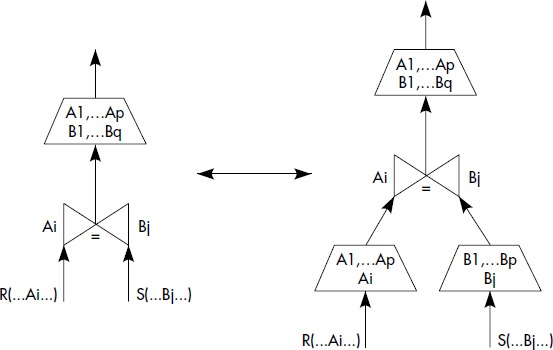
- Quasi-commutativité des projections et des jointures ;
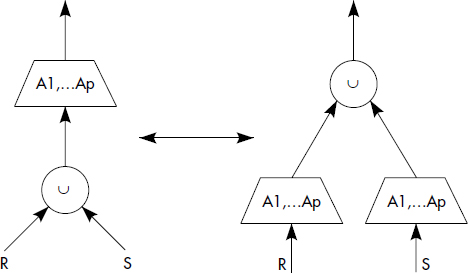
- Commutativité des projections avec les unions.
Notez que dans toutes les règles où figurent des jointures, celles-ci peuvent être remplacées par des produits cartésiens qui obéissent aux mêmes règles. En effet, le produit cartésien n'est jamais qu'une jointure sans critère. La quasi-commutativité signifie qu'il y a en général commutativité, mais que quelques précautions sont nécessaires pour éviter par exemple la perte d'attributs, ou qu'une opération commutée ne soit effectuée que sur l'une des relations.
- Regroupement des restrictions
- Quasi-commutativité des restrictions et projections (l'attribut de restriction doit être conservé par la projection)
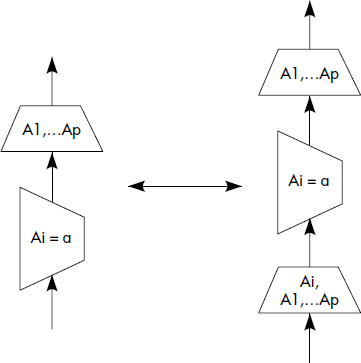
- Quasi-commutativité des restrictions et des jointures (la restriction est appliquée sur la relation contenant l'attribut restreint)
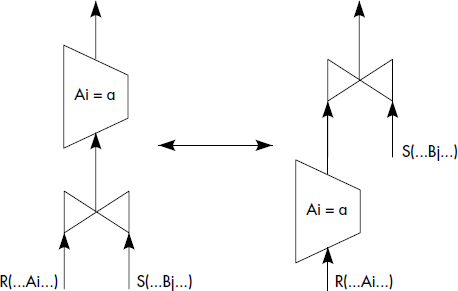
- Commutativité des restrictions avec les unions, intersections ou différences
- Quasi-commutativité des projections et jointures (la projection ne doit pas perdre les attributs de jointure)
- Commutativité des projections avec les unions
XV-3-2-2. Ordonnancement par descente des opérations unaires▲
Une première optimisation simple consiste à exécuter tout d'abord les opérations unaires (restriction, projection), puis les opérations binaires (jointure, produit cartésien, union, intersection, différence). En effet, les opérations unaires sont des réducteurs de la taille des relations, alors qu'il n'en est pas ainsi de certaines opérations binaires qui ont tendance à accroître la taille des résultats par rapport aux relations arguments. Par exemple, une jointure peut générer une très grande relation. Ceci se produit lorsque de nombreux tuples de la première relation se composent à de nombreux de la seconde. À la limite, elle peut se comporter comme un produit cartésien si tous les couples de tuples des deux relations vérifient le critère de jointure.
Aussi, afin de ne considérer que les arbres à flux minimal de données et de réduire ainsi le nombre d'entrées-sorties à effectuer, on est conduit à descendre les restrictions et projections. De plus, quand deux projections successives portent sur une même relation, il est nécessaire de les regrouper afin d'éviter un double accès à la relation. De même pour les restrictions. Ces principes précédents conduisent à l'algorithme d'optimisation suivant :
- Séparer les restrictions comportant plusieurs prédicats à l'aide de la règle 4 appliquée de la droite vers la gauche.
- Descendre les restrictions aussi bas que possible à l'aide des règles 5, 6, et 7.
- Regrouper les restrictions successives portant sur une même relation à l'aide de la règle 4 appliquée cette fois de la gauche vers la droite.
- Descendre les projections aussi bas que possible à l'aide des règles 8 et 9.
- Regrouper les projections successives à partir de la règle 3 et éliminer d'éventuelles projections inutiles qui auraient pu apparaître (projection sur tous les attributs d'une relation).
Pour simplifier les arbres et se rapprocher des opérateurs physiques réellement implémentés dans les systèmes, une restriction suivie par une projection est notée par un unique opérateur de sélection (restriction + projection) ; celui-ci permet d'éviter deux passes sur une même relation pour faire d'abord la restriction puis la projection. Il en est de même pour une jointure suivie par une projection : on parle alors d'opérateur de jointure-projection.
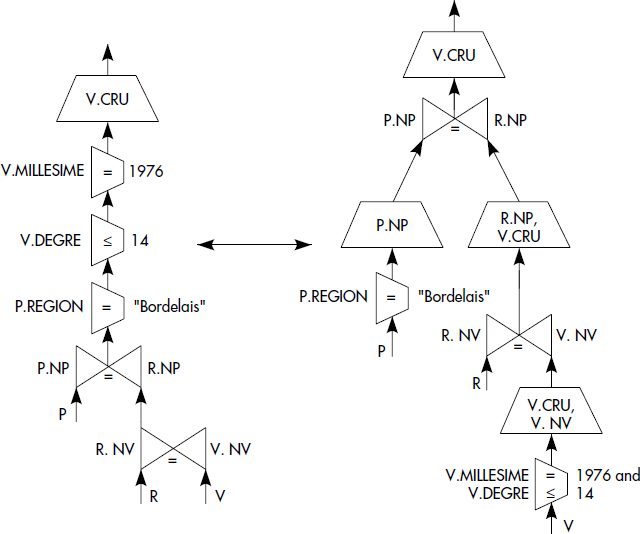
À titre d'illustration, l'algorithme de descente des restrictions et des projections a été appliqué à l'arbre de la figure X.2. On aboutit à l'arbre représenté figure X.9. Cet arbre n'est pas forcément optimal pour au moins deux raisons : la descente des restrictions et des projections n'est qu'une heuristique et l'ordre des opérations binaires n'a pas été optimisé.
XV-3-3. ORDONNANCEMENT PAR DÉCOMPOSITION▲
La décomposition est une stratégie d'ordonnancement qui fut appliquée dans le système INGRES [Wong76]. Elle est basée sur deux techniques de transformation de questions appelées détachement et substitution. Appliqué récursivement, le détachement permet d'ordonner les opérations selon l'ordre sélection, semi-jointure, et enfin jointure. La substitution consiste simplement à évaluer une question portant sur une relation en l'appliquant sur chacun des tuples de la relation. Cette technique revient donc au balayage et nous n'insisterons pas dessus. Le détachement permet par contre un premier ordonnancement des jointures.
XV-3-3-1. Le détachement de sous-questions▲
Le détachement permet de décomposer une question Q en deux questions successives Q1 et Q2, ayant en commun une variable unique résultat de Q1. C'est une transformation de question consistant à diviser une question en deux sous-questions successives ayant une seule table commune. De manière plus formelle, la situation générale où le détachement est possible est la suivante. Soit une question QT de la forme :
SELECT T(X1, X2 …, Xm)
FROM R1 X1, R2 X2…, Rn Xn
WHERE B2(X1, X2 …, Xm)
AND B1(Xm, Xm+1 …, Xn)B1 et B2 sont des qualifications incluant respectivement les variables X1,X2… Xm et Xm, Xm+1… Xn, alors que T est un résultat de projection à partir des variables X1, X2… Xm.
Une telle question peut être décomposée en deux questions, q1 suivie de q2, par détachement :
SELECT K(Xm) INTO R'm
FROM RM Xm, Rm+1Xm+1… Rn Xn
WHERE B1 (Xm, Xm+1, … Xn)K(Xm) contient les informations de Xm nécessaires à la deuxième sous-question :
SELECT T(X1, X2, … Xm)
FROM R1 X1, R2 X2 … R'mXm
WHERE B2(X1, X2, … Xm)Le détachement consiste en fait à transformer une question en deux questions imbriquées q1 et q2 qui peuvent être écrites directement en SQL comme suit :
SELECT T(X1, X2, … Xm)
FROM R1 X1, R2 X2 … Rm X'm
WHERE B2(X1, X2, … Xm) AND K(X'm) IN
SELECT K(Xm)
FROM RM Xm, Rm+1 Xm+1 … Rn Xn
WHERE B1 (X m, Xm+1, … Xn)Les questions n'ayant pas de variables communes, il est possible d'exécuter la question interne q1, puis la question externe q2.
Une question dans laquelle aucun détachement n'est possible est dite irréductible. On peut montrer qu'une question est irréductible lorsque le graphe de connexion des relations ne peut être divisé en deux classes connexes par élimination d'un arc [Wong76].
XV-3-3-2. Différents cas de détachement▲
Comme indiqué plus haut, certaines techniques d'optimisation de questions cherchent à exécuter tout d'abord les opérations qui réduisent la taille des relations figurant dans la question. Une telle opération correspond souvent à une sélection (restriction suivie de projection), mais parfois aussi à une semi-jointure [Bernstein81].
Notion X.12 : Semi-jointure (Semi-join)
La semi-jointure de la relation R par la relation S, notée R ![]() S, est la jointure de R et S projetée sur des attributs de R.
S, est la jointure de R et S projetée sur des attributs de R.
Autrement dit, la semi-jointure de R par S est composée de tuples (ou partie de tuples) de R qui joignent avec S. On peut aussi voir la semi-jointure comme une généralisation de la restriction : cette opération restreint les tuples de R par les valeurs qui apparaissent dans le (ou les) attribut(s) de jointure de S (par la projection de S sur ce (ou ces) attribut(s)). La semi-jointure R ![]() S est donc une opération qui réduit la taille de R, tout comme une restriction.
S est donc une opération qui réduit la taille de R, tout comme une restriction.
Le détachement permet de faire apparaître d'une part les restrictions, d'autre part les semi-jointures. Ce sont les deux seuls cas de détachement possibles. Nous allons illustrer ces détachements sur la question Q1 déjà vue ci-dessus :
SELECT DISTINCT V.CRU
FROM PRODUCTEURS P, VINS V, PRODUIT R
WHERE V.MILLESIME = 1976 AND V.DEGRE ≤ 14
AND P.REGION = "BORDELAIS" AND P.NP = R.NP
AND R.NV = V.NVLe graphe de connexion des relations de cette question est représenté figure X.4.
Tout d'abord, les deux sélections :
SELECT V.NV INTO V1
FROM VINS V
WHERE V.DEGRE ≤ 14 AND V.MILLESIME = 1976et
SELECT P.NP INTO P1
FROM PRODUCTEURS P
WHERE P.REGION = "BORDELAIS"peuvent être détachées.
En faisant maintenant varier V sur la relation V1 résultat de Q11 et P sur la relation P1 résultat de Q12, il reste à exécuter la question :
SELECT DISTINCT V.CRU
FROM P1 P, V1 V, PRODUIT R
WHERE P.NP = R.NP
AND R.NV = V.NVL'arc du graphe des relations correspondant à la jointure P.NP = R.NP peut ensuite être enlevé, ce qui correspond au détachement de la sous-question :
SELECT R.NV INTO R1
FROM P1 P, PRODUIT R
WHERE P.NP = R.NPq13 est bien une semi-jointure. Finalement, en faisant varier R sur la relation R1 résultat de q13, il ne reste plus qu'à exécuter une dernière semi-jointure :
SELECT DISTINCT V.CRU
FROM V1 V, R1 R
WHERE V.NV = R.NVQ1 a été décomposée en une suite de sélections et semi-jointures ((q11 | q12) ; q13 ; q14). q11 et q12 peuvent être exécutées en parallèle, puis q13 peut l'être, et enfin q14.
Toutes les questions ne sont pas ainsi décomposables en sélections suivies par des semi-jointures. Il est toujours possible de détacher les sélections. Par contre, [Bernstein81][Bernstein81] a montré que seules les questions dont les graphes de connexion après élimination des boucles (détachement des sélections) sont des arbres peuvent être décomposées en séquences de semi-jointures (d'ailleurs pas uniques). Les questions irréductibles présentent donc des cycles dans le graphe de connexion des relations. Cependant, certaines questions peuvent paraître irréductibles alors qu'il existe des questions équivalentes décomposables par détachement .
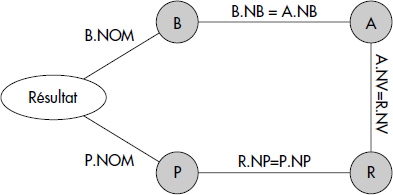
Il existe donc des questions qui ne peuvent être ramenées à des questions monovariables par détachement : celles qui présentent des cycles dans le graphe de connexion des attributs. En fait, ces questions retrouvent des résultats à partir de plusieurs relations et comportent donc de vraies jointures, non transformables en semijointures. Par exemple, la question Q4 qui recherche les couples (noms de buveurs, noms de producteurs) tels que le buveur ait bu un vin du producteur :
SELECT B.NOM, P.NOM
FROM BUVEURS B, ABUS A, PRODUIT R, PRODUCTEUR P
WHERE B.NB = A.NB AND A.NV = R.NV AND R.NP = P.NPest une question irréductible. Son graphe de connexion des relations présente en effet un cycle, comme le montre la figure X.10.
Afin de résoudre les questions irréductibles, le système INGRES de l'Université de Berkeley appliquait une méthode très simple : une des relations était balayée séquentiellement, par substitution des tuples successifs à la variable. Pour chaque tuple ainsi obtenu, la sous-question générée par substitution de la variable par le tuple lu était traitée par détachement. En cas de génération d'une nouvelle sous-question irréductible, la substitution était à nouveau appliquée. L'algorithme était donc récursif [Wong76]. Des méthodes de jointures beaucoup plus sophistiquées sont aujourd'hui disponibles.
XV-3-4. BILAN DES MÉTHODES D'OPTIMISATION LOGIQUE▲
Les méthodes de réécriture travaillant au niveau des opérateurs logiques sont suffisantes pour traiter les problèmes de correction de requêtes. Du point de vue optimisation, elles permettent d'ordonner les opérateurs à l'aide d'heuristiques simples. Les unions peuvent être accomplies avant les jointures. L'intersection et la différence ne sont que des cas particuliers de jointures.
La décomposition est une heuristique d'ordonnancement sophistiquée qui consiste à exécuter tout d'abord les sélections, puis à ordonner les jointures de sorte à faire apparaître en premier les semi-jointures possibles. Puisque les semi-jointures réduisent les tailles des relations, on peut ainsi espérer réduire les tailles des résultats intermédiaires et donc le nombre d'entrées-sorties. Cette heuristique apparaît ainsi comme supérieure à l'ordonnancement par restructuration algébrique qui n'ordonne pas du tout les jointures.
Le vrai problème est celui d'ordonner les jointures, et plus généralement les opérations binaires. La réécriture est une première approche qui permet un certain ordonnancement et ne nécessite aucune estimation de la taille des résultats des jointures. Cette approche est tout à fait insuffisante pour obtenir un plan d'exécution de coût minimal, car elle ne permet ni d'ordonner les opérations de manière optimale, ni de choisir les algorithmes optimaux pour chaque opération.
XV-4. LES OPÉRATEURS PHYSIQUES▲
Avant d'aborder l'optimisation physique, il est nécessaire de comprendre les algorithmes exécutant l'accès aux tables. Ceux-ci réalisent les opérateurs relationnels et sont au centre du moteur du SGBD responsable de l'exécution des plans. En conséquence, leur optimisation est importante. Dans la suite, nous nous concentrons sur la sélection, le tri, la jointure et les calculs d'agrégats. Les autres opérations ensemblistes peuvent être effectuées de manière analogue à la jointure.
XV-4-1. OPÉRATEUR DE SÉLECTION▲
Le placement des données dans les fichiers est effectué dans le but d'optimiser les sélections les plus fréquentes, et aussi les jointures. La présence d'index sur les attributs référencés dans le prédicat argument de la sélection change radicalement l'algorithme de sélection. Cependant, il existe des cas dans lesquels l'utilisation d'index est pénalisante, par exemple si la sélectivité du prédicat est mauvaise (plus de 20 % des tuples satisfont le critère). De plus, aucun index n'est peut-être spécifié. En résumé, on doit donc considérer deux algorithmes différents : la sélection par balayage séquentiel et par utilisation d'index.
XV-4-1-1. Sélection sans index▲
Le balayage séquentiel (sequential scan) nécessite de comparer chaque tuple de la relation opérande avec le critère. Si celui-ci est vrai, les attributs utiles sont conservés en résultat. La procédure effectue donc à la fois restriction et projection.
Le critère peut être compilé sous la forme d'un automate afin d'accélérer le temps de parcours du tuple. L'automate peut être vu comme une table ayant en colonnes les codes caractères et en lignes les états successifs. Il permet pour chaque caractère lu d'appliquer une action et de déterminer l'état suivant de l'automate. L'état suivant est soit continuation, soit échec, soit succès. En cas de continuation, le caractère suivant est traité. Sinon, le tuple est retenu en cas de succès, ou ignoré en cas d'échec. La figure X.11 illustre l'automate qui peut être utilisé pour traiter le critère COULEUR = "ROUGE" OU COULEUR = "ROSE". Des filtres matériels ont été réalisés selon ce principe afin d'effectuer la sélection en parallèle à l'entrée-sortie disque. Les SGBD effectuent plutôt le filtrage en mémoire après avoir lu une page du fichier en zone cache.
Un paramètre important pour la sélection sans index est le fait que le fichier soit trié ou non sur l'attribut de restriction. Dans le cas où le fichier n'est pas trié, le balayage séquentiel (BS) complet du fichier est nécessaire. Le nombre d'entrées-sorties nécessaires est alors le nombre de pages du fichier : Coût(BS) = Page(R).
Dans le cas où le fichier est trié sur l'attribut testé, une recherche dichotomique (RD) est possible : le bloc médian du fichier sera d'abord lu, puis selon que la valeur cherchée de l'attribut est inférieure ou supérieure à celle figurant dans le premier tuple du bloc, on procédera récursivement par dichotomie avec la première ou la seconde partie du fichier. Quoi qu'il en soit, la recherche sans index est longue et conduit à lire toutes les pages du fichier si celui-ci n'est pas trié, ou Log2(Page(R)) pages si le fichier est trié sur l'attribut de sélection : Coût(RD) = Log2(Page(R)).
XV-4-1-2. Sélection avec index de type arbre-B▲
Un index associe les valeurs d'un attribut avec la liste des adresses de tuples ayant cette valeur. Il est généralement organisé comme un arbre-B et peut être plaçant, c'est-à-dire que les tuples sont placés dans les pages selon l'ordre croissant des valeurs de clé dans l'index. Il s'agit alors d'un arbre-B+ ; celui-ci peut être parcouru séquentiellement par ordre croissant des clés. Dans les bases de données relationnelles, l'index primaire est souvent plaçant, alors que les index secondaires ne le sont pas.
Voici maintenant le principe d'évaluation d'un critère dont certains attributs sont indexés. On choisit les index intéressants (par exemple, ceux correspondant à une sélectivité du sous-critère supérieure à 60 %). Pour chacun, on construit une liste d'adresses de tuples en mémoire. Puis on procède aux intersections (critère ET) et aux unions (critère OU) des listes d'adresses. On obtient ainsi la liste des adresses de tuples qui satisfont aux sous-critères indexés. On peut ensuite accéder à ces tuples et vérifier pour chacun le reste du critère par un test en mémoire.
Certains systèmes retiennent seulement le meilleur index et vérifient tout le reste du critère en lisant les tuples sélectionnés par le premier index. Si un index est plaçant, on a souvent intérêt à l'utiliser comme critère d'accès. Un cas dégénéré est le cas de placement par hachage. Alors, seul le sous-critère référençant l'attribut de hachage est en général retenu et le reste est vérifié en mémoire.
La figure X.12 illustre une table VINS placée en séquentielle et possédant deux index sur CRU et DEGRE. Pour simplifier, le numéro de vin a été porté à la place des adresses relatives dans les entrées des index secondaires. Aucun index n'est plaçant. Le traitement du critère (CRU = "CHENAS") AND (MILLESIME ≥ 1986) AND (DEGRE = 12) conduit à considérer les deux index. On retient les index sur CRU et DEGRE, et l'on effectue la vérification du millésime par accès au fichier. D'où le plan d'accès indiqué figure X.12.
En général, le choix des meilleurs chemins d'accès (index ou fonction de hachage) n'est pas évident. Par exemple, on pourrait croire que les index sont inutiles dans les cas de comparateurs inférieur (<) ou supérieur (>). Il n'en est rien au moins pour les index plaçants : l'accès à l'index permet de trouver un point d'entrée dans le fichier que l'on peut ensuite balayer en avant ou en arrière en profitant du fait qu'il est trié. Les index non plaçants peuvent parfois être utiles avec des comparateurs supérieurs ou inférieurs, mais ceci est plus rare, car ils provoquent des accès désordonnés au fichier. Tout cela montre l'intérêt d'un modèle de coût qui permet seul de faire un choix motivé, comme nous le verrons ci-dessous.
PLAN D'ACCÉS
(table VINS critère (CRU = "CHENAS") AND (MILLESIME ≥ 1986) AND (DEGRE = 12))
{ C = LIRE (index CRU entrée CHENAS)
D = LIRE (index DEGRE entrée 12)
L = UNION (C, D)
Pour chaque l de L faire
{ Tuple = LIRE (table VINS adresse l)
if Tuple.MILLESIME ≥ 1986 alors
résultat = UNION (résultat, Tuple)}
}
}XV-4-2. OPÉRATEUR DE TRI▲
Le tri est un opérateur important, car il est utilisé pour les requêtes demandant une présentation de résultats triés, mais aussi pour éliminer les doubles, effectuer certaines jointures et calculer des agrégats.
Le tri de données qui ne tiennent pas en mémoire est appelé tri externe. Des algorithmes de tri externes ont été proposés bien avant l'avènement des bases de données relationnelles [Knuth73]. On distingue les algorithmes par tri-fusion (sort - merge) et les algorithmes distributifs. Les algorithmes par tri-fusion créent des monotonies en mémoire. Par exemple, si (B+1) pages sont disponibles, des monotonies de B pages sont créées, sauf la dernière qui comporte en général moins de pages. Le nombre de monotonies créées correspond au nombre de pages de la relation R à créer divisé par B en nombre entier, plus la dernière :
Nmon = 1+ ENT(Page(R)/B).Pour constituer une monotonie, au fur et à mesure des lectures d'enregistrements, un index trié est créé en mémoire. Lorsque les B pages ont été lues, les enregistrements sont écrits par ordre croissant des clés dans un fichier qui constitue une monotonie. La constitution de toutes les monotonies nécessite de lire et d'écrire la relation, donc 2*Page(R) entrées-sorties.
Dans une deuxième phase, les monotonies sont fusionnées. Comme seulement B pages en mémoire sont disponibles pour lire les monotonies, il faut éventuellement plusieurs passes pour créer une monotonie unique. Le nombre de passes nécessaires est LOGB(Nmon). Chaque passe lit et écrit toutes les pages de la relation. D'où le nombre total d'entrées-sorties pour un tri-fusion :
Coût(TF) = 2*Page(R)*(1+LOGB(1+ ENT(Page(R)/B)))Lorsque Page(R) est grand, un calcul approché donne :
Coût(TF) = 2*Page(R)*(1+LOGB(Page(R)/B)))On obtient :
Coût(TF) = 2*Page(R)*LOGB(Page(R))XV-4-3. OPÉRATEUR DE JOINTURE▲
Comme avec les sélections, il est possible de distinguer deux types d'algorithmes selon la présence d'index sur les attributs de jointure ou non. Dans la suite, nous développons les principes des algorithmes de jointure sans index puis avec index. Nous considérons l'équi-jointure de deux relations R1 et R2 avec un critère du type R1.A = R2.B, où A et B sont respectivement des attributs de R1 et R2. Dans le cas d'inéqui-jointure (par exemple, R1.A > R2.B), les algorithmes doivent être adaptés, à l'exception des boucles imbriquées qui fonctionnent avec tout comparateur. Nous supposons de plus que R1 a un nombre de tuples inférieur à celui de R2.
XV-4-3-1. Jointure sans index▲
En l'absence d'index, il existe trois algorithmes fondamentaux : les boucles imbriquées, le tri-fusion et le hachage [Blasgen76, Valduriez84, DeWitt84]. Les algorithmes hybrides sont souvent les plus efficaces [Fushimi86, DeWitt92].
4.3.1.1. Boucles imbriquées
L'algorithme des boucles imbriquées est le plus simple. Il consiste à lire séquentiellement la première relation R1 et à comparer chaque tuple lu avec chaque tuple de la deuxième R2. R1 est appelée relation externe et R2 relation interne. Pour chaque tuple de R1, on est donc amené à lire chaque tuple de R2. L'algorithme est schématisé figure X.13. L'opérateur + permet de concaténer les deux tuples opérandes. Le test d'égalité des attributs Tuple1.A et Tuple2.B doit être remplacé par la comparaison des attributs en cas d'inéqui-jointure.
Les entrées-sorties s'effectuant par page, en notant Page(R) le nombre de pages d'une relation R, on obtient un coût en entrées-sorties de :
Coût(BI) = Page(R1) + Page(R1) * Page(R2).
Si la mémoire cache permet de mémoriser (B+1) pages, il est possible de garder B pages de R1 en mémoire et de lire R2 seulement Page(R1)/B fois.
La formule devient alors :
Coût(BI) = Page(R1) + Page(R1)* Page(R2)/BCeci souligne l'intérêt d'une grande mémoire cache qui permet de réduire le nombre de passes.
Boucles_Imbriquées (R1,A, R2,B){
Pour chaque page B1 de R1 faire{
Lire (R1,B1) ;
Pour chaque page B2 de R2 faire{
Lire (R2,B2) ;
Pour chaque tuple Tuple1 de B1 faire{
Pour chaque tuple Tuple2 de B2 faire{
si Tuple1.A = Tuple2.B alors
ECRIRE(Résultat, Tuple1 + Tuple2) ;
}
}
}
}4.3.1.2. Tri-fusion
L'algorithme par tri-fusion effectue le tri des deux relations sur l'attribut respectif de jointure. Ensuite, la fusion des tuples ayant même valeur est effectuée. L'algorithme est schématisé figure X.14. En supposant des tris de N pages en 2N LOG N comme ci-dessus, le coût en entrées-sorties de l'algorithme est :
Coût(JT) = 2*Page(R1)*LOG(Page(R1)) + 2*Page(R2)*LOG(Page(R2)) + Page(R1) + Page(R2)Les logarithmes (LOG) sont à base 2 pour des tris binaires, et à base B pour des tris avec (B+1) pages en mémoire cache. L'algorithme est en général beaucoup plus efficace que le précédent. Son efficacité dépend cependant de la taille mémoire disponible. Soulignons aussi que si l'une des relations est déjà triée sur l'algorithme de jointure, il n'est pas nécessaire de refaire le tri.
Tri_Fusion (R1,A, R2,B){
R1T = TRIER (R1,A) ;
R2T = TRIER (R2,B) ;
Résultat = FUSIONNER (R1T,R2T)
}4.3.1.3. Partition
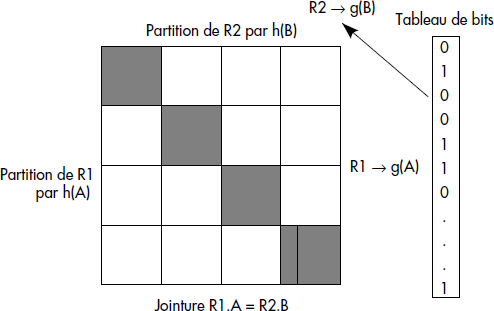
Il s'agit d'une méthode par hachage qui peut aisément être combinée avec l'une des précédentes. L'algorithme par partition consiste à découper les deux relations en partitions en appliquant une même fonction de hachage h sur les attributs de jointure A et B. Dans la mesure du possible, les partitions générées sont gardées en mémoire. On est alors ramené à joindre les paquets de mêmes rangs par l'un des algorithmes précédents. En effet, pour pouvoir être joints, deux tuples doivent donner la même valeur par la fonction de hachage appliquée aux attributs de jointure, car ceux-ci doivent être égaux.
L'algorithme peut être amélioré par la gestion d'un tableau de bits de dimension N en mémoire [Babb79] (N aussi grand que possible). L'astuce consiste à hacher la première relation simultanément avec la fonction h pour créer les partitions et une autre fonction g distribuant uniformément les valeurs de A sur [1,N]. La fonction g permet de maintenir un tableau de bits servant de filtre pour la deuxième relation. À chaque tuple haché de R1, le bit g(B) est mis à 1 dans le tableau de bits. Lorsqu'on partitionne la deuxième relation, on effectue pour chaque tuple de R2 un test sur le bit g(B) du tableau. S'il est à 0, on peut éliminer ce tuple qui n'a aucune chance de jointure (aucun tuple de R1 ne donne la même valeur par g). Le principe de l'algorithme par hachage est représenté figure X.15 : seuls les paquets de même rang, donc de la diagonale, sont joints.
4.3.1.4. Hachage
L'algorithme par hachage le plus simple consiste à hacher seulement la première relation dans un fichier haché, si possible gardé en mémoire. Ensuite, on balaye la deuxième relation, et pour chaque tuple lu on tente d'accéder au fichier haché en testant l'existence d'enregistrements de clé identique dans le fichier haché (fonction PROBE). Tant que l'on trouve des enregistrements de clé similaire, on compose la jointure résultat. Cet algorithme est schématisé figure X.16.
Hachage (R1,A, R2,B) {
Pour chaque page B1 de R1 faire {// hacher R1 sur A
Lire (R1,B1) ;
Pour chaque tuple Tuple1 de B1 faire{
p = h(Tuple1,A) ;
ECRIRE (Fichier_Haché, Paquet p, Tuple1) ;
}}
Pour chaque page B2 de R2 faire {// Parcourir R2
Lire (R2,B2) ;
Pour chaque tuple Tuple2 de B2 faire {
Tant que PROBE(Fichier_Haché,Tuple2) faire {
// Joindre si succès
ACCEDER (Fichier_Haché, Tuple1) ;
si Tuple1.A = Tuple2.B alors
ECRIRE(Résultat,Tuple1 + Tuple2) ;
}
}
}
}Le coût de l'algorithme par hachage dépend beaucoup de la taille mémoire disponible. Au mieux, il suffit de lire les deux relations. Au pire, on est obligé de faire plusieurs passes pour hacher la première relation, le nombre de passes étant le nombre de paquets de la table hachée divisé par le nombre de paquets disponibles en mémoire. On peut estimer ce nombre par Page(R1)/B, B+1 étant toujours le nombre de pages disponibles en mémoire. On obtient donc Page(R1)*Page(R1)/B entrées-sorties pour hacher R1. Il faut ensuite lire R2. Pour chaque tuple de R2, on va accéder au fichier haché. Notons Tuple(R) le nombre de tuples d'une relation R. Pour l'accès au fichier haché, on obtient un coût maximal de Tuple(R2) entrées-sorties, en négligeant l'effet de la mémoire cache. L'utilisation additionnelle d'un tableau de bits permet de diminuer Tuple(R2) d'un facteur difficile à évaluer, noté f avec f < 1, qui dépend de la sélectivité de la jointure. Ce facteur peut aussi intégrer l'effet de la mémoire cache. On obtient donc au total :
Coût(JH) = Page(R1)*Page(R1)/B + Page(R2) + f*Tuple(R2)Ceci est difficilement comparable avec les formules précédentes, mais très bon si B est grand et la sélectivité de la jointure faible (f petit).
4.3.1.5. Table de hachage
Une variante souvent utilisée de l'algorithme précédent consiste à construire en mémoire une table de hachage pour la plus petite relation. Cette table remplace le fichier haché et conserve seulement l'adresse des enregistrements, et pour chacun d'eux la valeur de l'attribut de jointure. La deuxième phase consiste à lire chaque tuple de la deuxième relation et à tester s'il existe des tuples ayant même valeur pour l'attribut de jointure dans la table de hachage. L'algorithme comporte donc une phase de construction (Build) de la table de hachage et une phase de tests (Probe) pour les tuples de la deuxième relation. La table de hachage mémorise pour chaque valeur de la fonction de hachage v la liste des adresses de tuples tels que H(A) = v, ainsi que la valeur de l'attribut A pour chacun des tuples. La table de hachage est généralement suffisamment petite pour tenir en mémoire. Le coût de l'algorithme est donc :
- Coût(TH) = Page(R1) + Page(R2) + Tuple(R1
 R2).
R2).
Le pseudocode de cet algorithme est représenté figure X.17. L'algorithme présente aussi l'avantage de permettre l'évaluation des requêtes en pipeline : dès que la table de hachage sur R1 a été construite, le pipeline peut être lancé lors du parcours séquentiel de R2. Nous considérons donc cet algorithme comme l'un des plus intéressants. Il peut être couplé avec la construction de partitions vue ci-dessus lorsque la table de hachage devient trop importante.
TableHachage (R1,A, R2,B) {
Pour i = 1, H faire TableH[i] = null ; // nettoyer la table de hachage
Pour chaque page B1 de R1 faire // construire la table de hachage {
Lire (R1,B1) ;
Pour chaque tuple Tuple1 de B1 faire Build(TableH,Tuple1, A) ;
} ;
// Parcourir R2 et tester chaque tuple
Pour chaque page B2 de R2 faire {
Lire (R2,B2) ;
Pour chaque tuple Tuple2 de B2 faire {
Tant que PROBE(TableH,Tuple2, B) faire {
// Joindre si succès
ACCEDER (TableH, AdresseTuple1) ; // obtenir adr.
LIRE (AdresseTuple1, Tuple1) ; // Lire le tuple
ECRIRE(Résultat,Tuple1||Tuple2) ; // Ecrire résultat
}
}
}
}XV-4-3-2. Jointure avec index de type arbre-B▲
Lorsque l'une des relations est indexée sur l'attribut de jointure (par exemple R1 sur A), il suffit de balayer la deuxième relation et d'accéder au fichier indexé pour chaque tuple. En cas de succès, on procède à la concaténation pour composer le tuple résultat. L'algorithme est analogue à la deuxième phase de l'algorithme par hachage en remplaçant le fichier haché par le fichier indexé. Le coût est de l'ordre de 3*Tuple(R2), en supposant trois accès en moyenne pour trouver un article dans le fichier indexé. Si R2 est grande, le coût peut être prohibitif et on peut avoir intérêt à créer un index sur R2 pour se ramener au cas suivant.
Lorsque les deux relations sont indexées sur les attributs de jointure, il suffit de fusionner les deux index [Valduriez87]. Les couples d'adresses de tuples joignants sont alors directement obtenus. L'algorithme est peu coûteux en entrées-sorties (lecture des index et des tuples résultats). Par contre, la mise à jour de ces index peut être pénalisante.
XV-4-4. LE CALCUL DES AGRÉGATS▲
Les algorithmes permettant de calculer les agrégats sont basés soit sur le tri, soit sur une combinaison du hachage et du tri. Un tri sur les attributs de groupement (argument du GROUP BY de SQL) permet de créer des monotonies correspondant à chaque valeur de ces attributs. Pour chaque monotonie, on applique les fonctions d'agrégat (COUNT, SUM, MIN, MAX, etc.) demandées. Un hachage préalable sur l'attribut de groupement permet de ramener le problème à un calcul d'agrégat dans chaque partition. L'approche est donc ici analogue à celle de la jointure par partition et tri présentée ci-dessus.
La présence d'index sur les attributs de groupement simplifie les calculs d'agrégats en permettant de créer les monotonies à partir de l'index. La présence d'un index sur l'attribut cible argument de la fonction est intéressante pour les cas minimum (MIN) et maximum (MAX). La première clé de l'index donne la valeur minimale et la dernière la valeur maximale. Il s'agit alors de partitionner l'index en fonction des attributs de groupement, ce qui peut s'effectuer en une passe de la relation si l'index tient en mémoire. Les meilleures optimisations d'agrégats, très importantes dans les systèmes décisionnels, passent par la mémorisation des calculs, par exemple dans des vues concrètes. Ces problèmes sont étudiés dans le chapitre consacré aux vues.
XV-5. L'ESTIMATION DU COÛT D'UN PLAN D'EXÉCUTION▲
La restructuration algébrique est insuffisante, car elle n'ordonne pas les opérations binaires. De plus, l'application d'une sélection initiale peut faire perdre un index qui serait utile pour exécuter une jointure. Afin d'aller au-delà, une solution pour choisir le meilleur plan d'exécution consiste à les générer tous, à estimer le coût d'exécution de chacun et à choisir celui de moindre coût. Malheureusement, une telle stratégie se heurte à plusieurs difficultés.
XV-5-1. NOMBRE ET TYPES DE PLANS D'EXÉCUTION▲
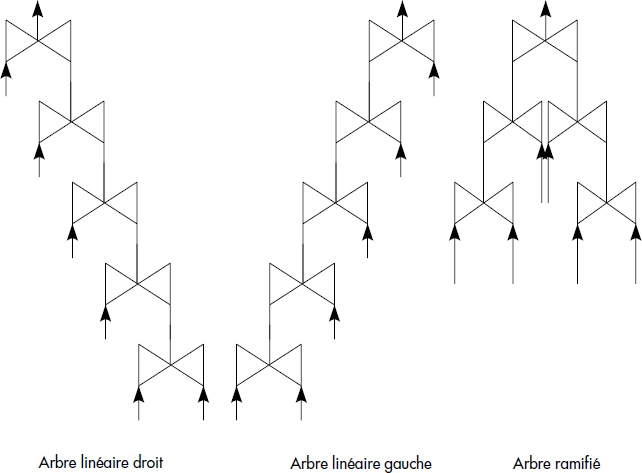
Tout d'abord, le nombre de plans d'exécution possibles est très grand. Cet inconvénient peut être évité en éliminant tous les plans qui font appel à l'opération de produit cartésien comme dans le fameux système R d'IBM ; en effet, la commutation de jointures peut générer des produits cartésiens qui, en général, multiplient les tailles des relations à manipuler. On a donc tout intérêt à éviter les plans d'exécution contenant des produits cartésiens. On peut aussi ne pas considérer les arbres ramifiés, mais seulement ceux contenant des jointures d'une relation de base avec une relation intermédiaire produite par les jointures successives. On parle alors d'arbre linéaire droit ou gauche (cf. figure X.18).
Une autre possibilité encore plus restrictive est d'éliminer tous les plans qui n'effectuent pas les sélections dès que possible. Ces heuristiques éliminant souvent des plans intéressants, on préfère aujourd'hui mettre en œuvre une stratégie d'exploration de l'espace des plans plus sophistiquée pour trouver un plan proche de l'optimal, comme nous le verrons ci-dessous.
Le nombre de plans devient vite très grand. En effet, considérons simplement le cas d'une requête portant sur n relations et effectuant donc (n-1) jointures. Soit P(n) le nombre de plans. Si l'on ajoute une relation, pour chaque jointure il existe deux positions possibles pour glisser la nouvelle jointure (à droite ou à gauche), et ce de deux manières possibles (nouvelle relation à droite ou à gauche) ; pour la jointure au sommet de l'arbre, il est aussi possible d'ajouter la nouvelle jointure au-dessus en positionnant la nouvelle relation à droite ou à gauche. Le nombre de jointures de n relations étant (n-1), il est possible de calculer :
P(n+1) = 4*(n-1) *P(n)+2*P(n) avec P(2) = 1D'où l'on déduit encore :
P(n+1) = 2*(2n-1)*P(n) avec P(2) = 1Il s'ensuit le nombre de plans possibles :
P(n+1) = (2n) ! / n !Un rapide calcul conduit au tableau suivant donnant le nombre de plans possibles P(n) pour n relations :
|
n |
P(n) |
|---|---|
|
2 |
2 |
|
3 |
12 |
|
4 |
120 |
|
5 |
1680 |
|
6 |
30240 |
|
7 |
665280 |
|
8 |
17297280 |
|
9 |
518918400 |
|
10 |
1,7643E+10 |
|
11 |
6,7044E+11 |
|
12 |
2,8159E+13 |
On voit ainsi que le nombre de plans devient rapidement très grand. Ce calcul ne prend pas en compte le fait que plusieurs algorithmes sont possibles pour chaque opérateur de jointure. Si a algorithmes sont disponibles, le nombre de plans pour n relations doit être multiplié par an-1. Ceci devient rapidement un nombre considérable.
Le calcul du coût d'un plan peut être effectué récursivement à partir de la racine N de l'arbre en appliquant la formule suivante, dans laquelle Filsi désigne les fils du nœud N :
COUT (PT) = COUT(N) + Σ COUT(FILSI)Le problème est donc de calculer le coût d'un nœud qui représente une opération relationnelle. La difficulté est que l'estimation du coût d'une opération nécessite, au-delà de l'algorithme appliqué, la connaissance de la taille des relations d'entrée et de sortie. Il faut donc estimer la taille des résultats intermédiaires de toutes les opérations de l'arbre considéré. Le choix du meilleur algorithme pour un opérateur nécessite d'autre part la prise en compte des chemins d'accès aux relations (index, placement, lien…) qui change directement ces coûts. Nous allons ci-dessous examiner les résultats concernant ces deux problèmes.
XV-5-2. ESTIMATION DE LA TAILLE DES RÉSULTATS INTERMÉDIAIRES▲
L'estimation de la taille des résultats est basée sur un modèle de distribution des valeurs des attributs dans chacune des relations, et éventuellement des corrélations entre les valeurs d'attributs. Le modèle doit être conservatif, c'est-à-dire que pour toute opération de l'algèbre relationnelle, il faut être capable, à partir des paramètres décrivant les relations arguments, de calculer les mêmes paramètres pour la relation résultat. Le modèle le plus simple est celui qui suppose l'uniformité de la distribution des valeurs et l'indépendance des attributs [Selinger79]. De telles hypothèses sont utilisées dans tous les optimiseurs de systèmes en l'absence d'informations plus précises sur la distribution des valeurs d'attributs. Un tel modèle nécessite de connaître au minimum :
- le nombre de valeurs d'un attribut A noté Tuple(A) ;
- les valeurs minimale et maximale d'un attribut A notées MIN(A) et MAX(A) ;
- le nombre de valeurs distinctes de chaque attribut A noté NDIST(A) ;
- le nombre de tuples de chaque relation R noté Tuple(R).
Le nombre de tuples d'une restriction est alors calculé par la formule :
TUPLE (σ(R)) = P(CRITERE) * TUPLE(R)où p(critère) désigne la probabilité que le critère soit vérifié, appelée facteur de sélectivité du prédicat de restriction.
Notion X.13 : Facteur de sélectivité (Selectivity factor)
Coefficient associé à une opération sur une table représentant la proportion de tuples de la table satisfaisant la condition de sélection.
Avec une hypothèse de distribution uniforme des valeurs d'attributs, le facteur de sélectivité peut être calculé comme suit :
p(A=valeur) = 1/NDIST(A)
p(A>valeur) = (MAX(A) - valeur)/(MAX(A) - MIN(A))
p(A<valeur) = (valeur - MIN(A))/(MAX(A) - MIN(A))
p(A IN liste) = (1/NDIST(A)) * Tuple(liste)
p(P et Q) = p(P) * p(Q)
p(P ou Q) = p(P) + p(Q) - p(P) * p(Q)
p(not P) = 1 - p(P)Le nombre de tuples d'une projection sur un groupe d'attributs X est plus simplement obtenu par la formule :
TUPLE (???? (R)) = (1-d) * TUPLE(R)avec d = probabilité de doubles. La probabilité de doubles peut être estimée en fonction du nombre de valeurs distinctes des attributs composant X ; une borne supérieure peut être obtenue par la formule :
d = (1-NDIST(A1)/Tuple(R))*(1-NDIST(A2)/Tuple(R)) …
* (1-NDIST(Ap)/Tuple(R)où A1, A2, …, An désignent les attributs retenus dans la projection.
La taille d'une jointure est plus difficile à évaluer en général. On pourra utiliser la formule :
- Tuple(R1
 R2) = p * Tuple(R1) * Tuple(R2)
R2) = p * Tuple(R1) * Tuple(R2)
où p, compris entre 0 et 1, est appelé facteur de sélectivité de la jointure. En supposant une équi-jointure sur un critère R1.A = R2.B et une indépendance des attributs A et B, le nombre de tuples de R2 qui joignent avec un tuple de R1 donné est au plus Tuple(R2)/NDIST(B). Pour tous les tuples de R1, on obtient donc Tuple(R1)*Tuple(R2)/NDIST(B) tuples dans la jointure. On en déduit la formule p = 1/NDIST(B). Mais en renversant l'ordre des relations, on aurait déduit la formule p = 1/NDIST(A). Ceci est dû au fait que certains tuples de R1 (et de R2) ne participent pas à la jointure, alors qu'ils ont été comptés dans chacune des formules. Une estimation plus raisonnable demanderait d'éliminer les tuples ne participant pas à la jointure. Il faudrait pour cela prendre en compte le nombre de valeurs effectives du domaine commun de A et B, nombre en général inconnu. On utilisera plutôt une borne supérieure de p donnée par la formule :
p = 1/ MIN(NDIST(A),NDIST(B))Les estimations de tailles des relations et attributs doivent être mémorisées au niveau de la métabase. Elles devraient théoriquement être mises à jour à chaque modification de la base. La plupart des systèmes ne mettent à jour les statistiques que lors de l'exécution d'une commande spécifique (RUNSTAT) sur la base. Afin d'affiner les estimations, il est possible de mémoriser des histogrammes de distribution des valeurs d'attributs dans la métabase. Ces valeurs sont calculées par des requêtes comportant des agrégats. Les formules précédentes sont alors appliquées pour chaque fraction de l'histogramme qui permet d'estimer le nombre de valeurs distinctes (NDIST) ou non (Tuple) dans une plage donnée.
XV-5-3. PRISE EN COMPTE DES ALGORITHMES D'ACCÈS▲
Chaque opérateur est exécuté en appliquant si possible le meilleur algorithme d'accès aux données. Le coût dominant d'un opérateur est le coût en entrées-sorties. Celui-ci dépend grandement des chemins d'accès disponibles, comme nous l'avons vu ci-dessus, lors de l'étude des opérateurs d'accès. Par exemple, en désignant toujours par Tuple(R) le nombre de tuples de la relation R, par Page(R) son nombre de pages, par (B+1) le nombre de pages disponibles en mémoire cache, nous avons pour la jointure par boucles imbriquées (BI) dans le cas sans index :
Coût(BI(R1,R2)) = Page(R1) + [Page(R1)/B]*Page(R2)S' il existe un index sur l'attribut de jointure de R2, le coût devient :
Coût(BI(R1,R2)) = Page(R1) + Tuple(R1)*I(R2)où I(R2) désigne le nombre moyen d'entrées-sorties pour accéder au tuple de R2 via l'index. I(R2) dépend du type d'index, de sa hauteur, de la mémoire centrale disponible pour l'index, et aussi du fait que R1 soit triée sur l'attribut de jointure ou non. En général, I(R2) varie entre 0.5 et la hauteur de l'index, 2 étant une valeur moyenne classique.
Au-delà des coûts en entrées-sorties, il faut aussi estimer les coûts de calcul, souvent négligés. Dans Système R [Selinger79], la détermination du plan d'exécution est effectuée en affectant un coût à chaque plan candidat calculé par la formule suivante :
COUT = NOMBRE D'ACCES PAGE + W*NOMBRE D'APPELS INTERNES.Le nombre d'appels internes donne une estimation du temps de calcul nécessaire à l'exécution du plan, alors que le nombre d'accès page évalue le nombre d'entrées-sorties nécessaires à l'exécution du plan. W est un facteur ajustable d'importance relative du temps unité centrale et du temps entrées-sorties. Le nombre d'accès page est estimé par évaluation d'un facteur de sélectivité F pour chacun des prédicats associés à une opération de l'algèbre relationnelle. Le nombre d'accès pour l'opération est calculé en fonction de F et de la taille des relations opérandes. Le calcul de F tient compte de la présence ou non d'index ; ainsi, par exemple, le facteur de sélectivité d'une sélection du type Attribut = valeur est estimé par :
F = 1/ Nombre d'entrées dans l'indexs'il existe un index et à 1/10 sinon.
XV-6. LA RECHERCHE DU MEILLEUR PLAN▲
L'optimisation physique permet de prendre en compte le modèle de coût afin de déterminer le meilleur plan, ou un plan proche de celui-là. Elle part d'un arbre en forme canonique, par exemple composé de sélections dont les critères sont sous forme normale conjonctive, puis de jointures, unions, intersections et différences, et enfin d'agrégats suivis encore d'éventuelles sélections/projections finales, certaines de ces opérations pouvant être absentes. Elle transforme cet arbre en un plan d'accès en choisissant les algorithmes pour chaque opérateur, et en modifiant éventuellement l'arbre afin de profiter de propriétés physiques de la base (index par exemple).
Comme vu ci-dessus, le nombre de plans d'exécution possibles peut être très grand pour des questions complexes. L'ensemble des plans possibles est appelé espace des plans. Afin d'éviter d'explorer exhaustivement cet espace de recherche, c'est-à-dire d'explorer tous les plans, les optimiseurs modernes sont construits comme des générateurs de plans couplés à une stratégie de recherche découlant des techniques d'optimisation de la recherche opérationnelle [Swami88].
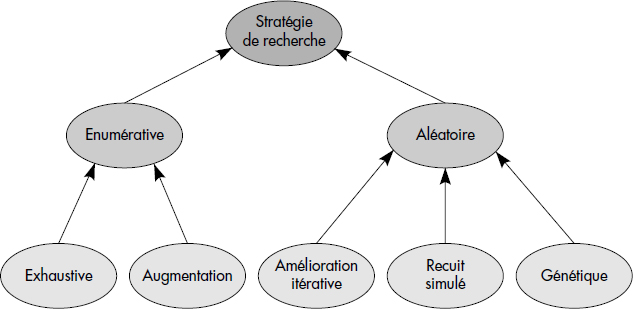
Notion X.14 : Stratégie de recherche (Search strategy)
Tactique utilisée par l'optimiseur pour explorer l'espace des plans d'exécution afin de déterminer un plan de coût proche du minimum possible.
Un optimiseur est fermé lorsque tous les opérateurs et algorithmes d'accès, ainsi que toutes les règles de permutation de ces opérateurs, sont connus à la construction du système. Les systèmes relationnels purs ont généralement des optimiseurs fermés. La stratégie de recherche dans les optimiseurs fermés est basée sur un algorithme déterministe, qui construit une solution pas à pas soit en appliquant une heuristique ou une méthode d'évaluation progressive permettant d'exhiber le meilleur plan, de type programmation dynamique. Nous étudions dans cette section quelques algorithmes de cette classe.
XV-6-1. ALGORITHME DE SÉLECTIVITÉ MINIMALE▲
Cet algorithme très simple consiste à compléter les optimisations logiques présentées ci-dessus, telles par exemple la descente des restrictions et projections, par un ordonnancement des jointures par ordre de sélectivité croissante. L'algorithme construit un arbre linéaire gauche en partant de la plus petite relation, et en joignant à chaque niveau avec la relation restante selon le plus petit facteur de sélectivité de jointure. Ainsi, les relations intermédiaires sont globalement gardées près du plus petit possible. Cet algorithme, représenté figure X.19 généralise la méthode de décomposition d'Ingres étudiée ci-dessus. Une variante peut consister à produire à chaque fois la relation de plus petite cardinalité. Pour chaque opération, l'algorithme de coût minimal est ensuite sélectionné. Ces algorithmes restent simples, mais sont loin de déterminer le meilleur plan.
Algorithme MinSel {
Rels = liste des relations à joindre ;
p = plus petite relation ;
Tant que Rels non vide {
R = relation de sélectivité minimum de Rels ;
p = join(R,p) ;
Rels = Rels - R ;
}
Retourner(p) ;
}XV-6-2. PROGRAMMATION DYNAMIQUE (DP)▲
La programmation dynamique est une méthode très connue en recherche opérationnelle, dont le principe est que toute sous-politique d'une politique optimale est optimale. Ainsi, si deux sous-plans équivalents du plan optimal cherché sont produits, il suffit de garder le meilleur et de le compléter pour atteindre le plan optimal. Cette technique, employée dans le système R [Selinger79] pour des plans sans produit cartésien, permet de construire progressivement le plan, par ajouts successifs d'opérateurs. L'algorithme commence par créer tous les plans monorelation, et construit des plans de plus en plus larges étape par étape. À chaque étape, on étend les plans produits à l'étape précédente en ajoutant un opérateur. Quand un nouveau plan est généré, la collection de plans produits est consultée pour retrouver un plan équivalent. Si un tel plan est trouvé, alors les coûts des deux plans sont comparés et seul celui de coût minimal est conservé. La figure X.20 décrit de manière plus précise l'algorithme connu sous le nom DP (Dynamic Programming). Cet algorithme assez simple devient très coûteux pour un nombre important de relations, si l'on considère tous les arbres possibles. La complexité est de l'ordre de 2N, où N est le nombre de relations. Il n'est donc que difficilement applicable au-delà d'une dizaine de relations [Swami88].
Algorithme DP {
PlanOuverts = liste de tous les plans monorelation possibles ;
Éliminer tous les plans équivalents exceptés les moins coûteux ;
Tant qu'il existe p ∈ PlanOuverts {
Enlever p de PlanOuverts ;
PlanOptimal = p ;
Pour chaque opérateur o permettant d'étendre p {
Étendre le plan p en ajoutant cet opérateur o ;
Calculer le coût du nouveau plan ;
Insérer le nouveau plan dans PlanOuverts ;
}
Éliminer tous les plans équivalents exceptés les moins coûteux ;
}
Retourner(PlanOptimal) ;
}XV-6-3. PROGRAMMATION DYNAMIQUE INVERSE▲
Une variante de l'algorithme précédent consiste à calculer récursivement la meilleure jointure possible parmi N relations, et ce selon tous les ordres possibles. Bien que récursif, l'algorithme est analogue au précédent, mais procède en profondeur plutôt qu'en largeur. Il a l'avantage de construire plus rapidement des résultats et peut ainsi être arrêté si le temps consacré à l'optimisation est dépassé. La figure X.21 illustre cet algorithme dans le cas des jointures.
Algorithme RDP (Rels) {
PlanOuverts = {} ;
Coût(MeilleurPlan) = ∞ ;
Pour chaque R in Rels{
RestRels = Rels - R ;
si RestRels = {} alors p = R sinon
p = R ▷◁ RDP(RestRels) ;
Insérer p dans PlanOuverts ;
si coût(p) ≤ coût(MeilleurPlan) alors MeilleurPlan = p ;
Éliminer tous les plans équivalents exceptés les moins coûteux ;
}
Retourner (MeilleurPlan) ;
}XV-6-4. LES STRATÉGIES DE RECHERCHE ALÉATOIRES▲
Les différentes stratégies de recherche sont classées selon une hiérarchie de spécialisation figure X.22. On distingue les stratégies énumératives des stratégies aléatoires. Les premières énumèrent systématiquement des plans possibles. La stratégie exhaustive les énumère tous. La stratégie par augmentation les construit progressivement en partant par exemple de la projection finale et en introduisant progressivement les relations, par exemple par ordre de taille croissante. Elle évitera en général les produits cartésiens et appliquera dès que possible restriction et projection.
Les stratégies aléatoires [Lanzelotte91] explorent aléatoirement l'espace des plans. L'amélioration itérative tire au hasard n plans (par exemple en permutant l'ordre des relations) et essaie de trouver pour chacun d'eux le plan optimal le plus proche (par exemple par descente des restrictions et projections, et choix des meilleurs index). L'optimum des plans localement optimum est finalement sélectionné. La stratégie du recuit simulé procède à partir d'un plan que l'on tente d'optimiser en appliquant des transformations successives. Les transformations retenues améliorent ce plan, excepté quelques-unes introduites afin d'explorer un espace plus large avec une probabilité variant comme la température du système (en e-1/T, où T est la température). La température est de fait une variable dont la valeur est très élevée au départ et qui diminue au fur et à mesure des transformations, de sorte à ne plus accepter de transformation détériorant le coût quand le système est gelé. Cette stratégie, bien connue en recherche opérationnelle, permet de converger vers un plan proche de l'optimum, en évitant les minimums locaux. On citera enfin les stratégies génétiques qui visent à fusionner deux plans pour en obtenir un troisième.
Toutes ces stratégies sont très intéressantes pour des systèmes extensibles, objet ou objet-relationnel. En effet, dans un tel contexte, le nombre de plans d'exécution devient très grand. Les choix sont donc très difficiles et les stratégies de type programmation dynamique deviennent d'application difficile. Voilà pourquoi nous étudierons les stratégies aléatoires plus en détail dans la partie III de cet ouvrage.
XV-7. CONCLUSION▲
Dans ce chapitre, nous avons étudié les algorithmes et méthodes de base pour l'évaluation efficace des requêtes dans les SGBD relationnels. L'étude a été réalisée à partir de requêtes exprimées en algèbre relationnelle. Pour réduire la complexité, nous avons décomposé le problème de l'optimisation en une phase logique fondée sur les techniques de réécriture et une phase physique basée sur un modèle de coût. De nos jours, la réalisation d'un optimiseur performant nécessite d'intégrer ces deux phases.
Nous nous sommes plus concentrés sur l'optimisation des requêtes avec jointures, car celles-ci sont très fréquentes et souvent coûteuses dans les bases de données relationnelles. Nous n'avons qu'esquissé l'optimisation des agrégats. Nous reviendrons sur ce problème dans les perspectives pour l'aide à la décision. Nous n'avons aussi qu'esquissé l'étude des stratégies de recherche aléatoires, qui permettent de trouver rapidement un plan satisfaisant dans des espaces de recherche très vastes. Nous reviendrons sur cet aspect dans le cadre des optimiseurs extensibles, mis en œuvre dans les SGBD objet et objet-relationnel, au moins en théorie. Dans ce contexte, les plans sont encore plus nombreux que dans les SGBD relationnels, et la stratégie devient un composant essentiel.
Les techniques abordées se généralisent au contexte des bases de données réparties et parallèles. Les techniques de base de l'approche multiprocesseurs consistent à diviser pour régner : les tables sont partitionnées sur plusieurs serveurs parallèles ou répartis, les requêtes sont divisées en sous-requêtes par l'évaluateur de requêtes. Le problème supplémentaire est d'optimiser les transferts entre serveurs. Ceux-ci s'effectuent par le biais d'une mémoire commune, d'un bus partagé ou d'un réseau, selon le contexte. Le modèle de coût doit prendre en compte ces transferts, et les algorithmes doivent être adaptés. Les fondements restent cependant identiques à ceux présentés dans ce chapitre.
XV-8. BIBLIOGRAPHIE▲
[Aho79] Aho A.V., Sagiv Y., Ullman J.D., « Equivalences among Relational Expressions », SIAM Journal of Computing, vol. 8, n° 2, p. 218-246, Juin 1979.
- Cet article définit formellement l'équivalence d'expressions algébriques et donne des conditions d'équivalence.
[Astrahan76] Astrahan M.M. et al., « System R : Relational Approach to Database Management », ACM TODS, vol. 1, n° 2, Juin 1976.
- Cet article de synthèse présente le fameux système R réalisé à San José, au centre de recherche d'IBM. Il décrit tous les aspects, en particulier l'optimiseur de requêtes, intéressant pour ce chapitre.
[Babb79] Babb E., « Implementing a Relational Database by Means of Specialized Hadware », ACM TODS, vol. 4, n° 1, Mars 1979.
- Auteur de la machine bases de données CAFS réalisée à ICL en Angleterre, E. Babb introduit en particulier les tableaux de bits afin d'accélérer les jointures par hachage.
[Bernstein81] Bernstein P.A., Chiu D.W., « Using Semijoins to Solve Relational Queries », Journal of the ACM, vol. 28, n° 1, p. 25-40, Janvier 1981.
- Cet article présente une étude approfondie de l'usage des semi-jointures pour résoudre les questions relationnelles. De multiples résultats basés sur l'étude du graphe des relations pour décomposer une requête en semi-jointures sont établis.
[Blasgen76] Blasgen M.W., Eswaran K.P., « On the Evaluation of Queries in Relational Systems », IBM Systems Journal, vol. 16, p. 363-377, 1976.
- Se fondant sur le développement et les expériences conduites autour de système R, les auteurs montrent que différents algorithmes de jointures doivent être considérés pour évaluer efficacement les requêtes dans les SGBD relationnels.
[Chakravarthy90] Chakravarthy U.S., Grant J., Minker J., « Logic Based Approach to Semantic Query Optimization », ACM Transactions on Database Systems, vol. 15, n° 2, p. 162-207, Juin 1990.
- Cet article démontre l'apport de contraintes d'intégrité exprimées en logique du premier ordre pour l'optimisation de requêtes. Il propose un langage d'expression de contraintes et des algorithmes de base pour optimiser les requêtes.
[DeWitt84] DeWitt D., Katz R., Olken F., Shapiro L., Stonebraker M., Wood D., « Implementation Techniques for Main Memory Databases », Proc. ACM SIGMOD Int. Conf. on Management of data, Boston, Mass., p. 1-8, Juin 1984.
- Les auteurs proposent différentes techniques pour la gestion de bases de données en mémoire. L'algorithme de hachage « Build and Probe » consiste à construire une table hachée en mémoire à partir de la première relation, puis à tester chaque tuple de la seconde relation contre cette table en appliquant la même fonction de hachage. Chaque entrée de la table contient un pointeur vers le tuple et la valeur de l'attribut de jointure, ce qui permet de tester le prédicat de jointure et de retrouver le tuple efficacement.
[DeWitt86] DeWitt D., Gerber R., Graefe G., Heytens M., Kumar K., Mualikrishna M., « Gamma - A high performance Dataflow Database Machine », Proc. 12th Intl. Conf. on Very Large Data Bases, Kyoto, Japan, Morgan Kaufman Ed., Septembre 1986.
- La machine GAMMA réalisée à l'Université de Madison explore les techniques de flot de données pour paralléliser les opérateurs de jointure. Les algorithmes de type pipeline ont été expérimentés pour la première fois sur un réseau local en boucle.
[DeWitt92] DeWitt D., Naughton J., Schneider D., Seshadri S., « Practical Skew Handling in Parallel Joins » Proc. 18th Intl. Conf. on Very Large Data Bases, Sydney, Australia, Morgan Kaufman Ed., Septembre 1992.
- Cet article étudie les effets des distributions biaisées de valeurs d'attributs de jointure sur les algorithmes de jointure. Les algorithmes hybrides semblent les plus résistants.
[Finance94] Finance B., Gardarin G., « A Rule-based Query Optimizer with Adaptable Search Strategies », Data and Knowledge Engineering, North-Holland Ed., vol. 3, n° 2, 1994.
- Les auteurs décrivent l'optimiseur extensible réalisé dans le cadre du projet Esprit EDS. Cet optimiseur est extensible grâce à un langage de règles puissant et dispose de différentes stratégies de recherche paramétrables.
[Fushimi86] Fushimi S., Kitsuregawa M., Tanaka H., « An Overview of the System Software of a Parallel Relational Database Machine : GRACE », Proc. 12th Int. Conf. on Very Large Data Bases, Kyoto, Japan, Morgan Kaufman Ed., Septembre 1986.
- Les auteurs présentent la machine bases de données GRACE. Celle-ci se distingue par son algorithme de jointure parallèle basé sur une approche mixte, combinant hachage et tri.
[Gardarin84] Gardarin G., Jean-Noël M., Kerhervé B., Mermet D., Pasquer F., Simon E., « Sabrina : un Système de Gestion de Bases de Données Relationnelles issu de la Recherche », Revue TSI, Dunod AFCET Ed., vol. 5, n° 6, 1986.
- Cet article décrit le SGBD SABRE réalisé à l'INRIA de 1980 à 1984, puis industrialisé et commercialisé par la société INFOSYS de 1984 à 1990. Ce SGBD disposait d'un optimiseur basé sur des heuristiques sophistiquées.
[Graefe93] Graefe G., « Query Evaluation Techniques for Large Databases », ACM Computer Surveys, vol. 25, n° 2, p. 73-170, Juin 1993.
- Un des plus récents articles de synthèse sur l'optimisation de requêtes. L'auteur présente une vue d'ensemble des techniques d'optimisation de requêtes, en mettant en avant leur comportement vis-à-vis de grandes bases de données.
[Gray91] Gray J., The Benchmark Handbook for Database and Transaction Processing Systems, 2nd edition, Morgan Kaufman, San Mateo, CA, 1991.
- Le livre de référence du Transaction Processing Council (TPC). Il présente les « benchmarks » de base, notamment TPC/A, TPC/B, TPC/C, et les conditions précises d'exécution de ces bancs d'essai.
[Haas89] Haas M.L., Freytag J.C., Lohman G.M., Pirahesh H., « Extensible Query Processing in Starbust », Proc. ACM SIGMOD Intl. Conf. On Management of Data, p. 377-388, 1989.
- Cet article présente l'optimiseur de Starbust, un système extensible réalisé à IBM. Cet optimiseur se décompose clairement en deux phases, la réécriture et le planning. Il est à la base des nouvelles versions de l'optimiseur de DB2.
[Hevner79] Hevner A.R., Yao B., « Query Processing in Distributed Database Systems », IEEE Transactions on Software Engineering, vol. 5, n° 3, p. 177-187, Mai 1979.
- Cet article présente une synthèse des techniques d'optimisation de requêtes connues à cette date dans les BD réparties. Il développe un modèle de coût incluant le trafic réseau.
[Jarke84] Jarke M., Koch J., « Query Optimization in Database Systems » ACM Computing Surveys, vol. 16, n° 2, p. 111-152, Juin 1984.
- Un des premiers articles de synthèse sur l'optimisation de requêtes dans les bases de données relationnelles. L'article suppose les questions exprimées en calcul relationnel de tuples. Il donne un cadre général pour l'évaluation de requêtes et couvre les algorithmes de réécriture logique, les méthodes d'optimisation physique, les modèles de coût, et plus généralement les principales techniques connues à cette époque.
[Kim85] Kim Won, Reiner S., Batory D., Query Processing in Database Systems, Springer-Verlag Ed., 1985.
- Ce livre de synthèse est composé d'une collection d'articles. À partir d'un chapitre de synthèse introductif, les auteurs développent différents aspects spécifiques : bases de données réparties, hétérogènes, objets complexes, optimisation multirequêtes, machines bases de données, modèle de coût, etc.
[King81] King J.J., « QUIST : A System for Semantic Query Optimization in Relational Data Bases », Proc. 7th Intl. Conf. on Very Large Data Bases, Cannes, France, IEEE Ed., p. 510-517, Sept. 1981.
- Cet article décrit l'un des premiers systèmes capables de prendre en compte les contraintes d'intégrité pour l'optimisation de requêtes.
[Knuth73] Knuth D.E., The Art of Computer Programming, Volume 3 : Sorting and Searching, Addison-Wesley, Reading, Mass., 1973.
- Le fameux livre de Knuth consacré aux algorithmes et structures de données pour les recherches et les tris.
[Rosenkrantz80] Rosenkrantz D.J., Hunt H.B., « Processing Conjunctive Predicates and Queries », Proc. 6th Intl. Conf. on Very Large Data Bases, Montréal, Canada, IEEE Ed., Septembre 1980.
- Cet article présente des techniques permettant de déterminer des questions contradictoires, équivalentes, ou incluses l'une dans l'autre. Les méthodes sont basées sur un graphe d'attribut normalisé où les arcs sont valués par des constantes. Un arc allant d'un nœud x à un nœud y correspond à l'inégalité x ≤ y+c. Une égalité est modélisée par deux arcs. Par exemple, une question est contradictoire s'il existe un cycle dont la somme des valuations est négative.
[Selinger79] Selinger P., « Access Path Selection in a Relational Database Management System », ACM SIGMOD Intl. Conf. On Management of Data, Boston, Mai 1979.
- Cet article décrit les algorithmes de sélection de chemin d'accès dans le système R. Il introduit le modèle de coût basé sur des distributions uniformes décrit section 5, et la méthode de sélection du meilleur plan basée sur la programmation dynamique.
[Smith75] Smith J.M., Chang P.Y., « Optimizing the performance of a Relational Algebra Database Interface », Comm. ACM, vol. 18, n° 10, p. 68-579, 1975.
- Les auteurs introduisent l'ensemble des règles de restructuration algébrique permettant d'optimiser logiquement les expressions de l'algèbre relationnelle.
[Stonebraker76] Stonebraker M., Wong E., Kreps P., Held G., « The Design and Implementation of Ingres », ACM TODS, vol. 1, n° 3, Septembre 1976.
- Cet article de synthèse présente le fameux système INGRES réalisé à l'université de Berkeley. Il décrit tous ses aspects, en particulier l'optimiseur de requêtes basé sur la décomposition de requêtes.
[Stonebraker87] Stonebraker M., « The Design of the Postgres Storage System », 13e Intl. Conf. on Very Large Data Bases, Morgan Kaufman Ed., Brighton, Angleterre, 1987.
- Postgres signifie « après Ingres ». M. Stonebraker a construit ce système à Berkeley après avoir réalisé et commercialisé le système Ingres. Postgres est original, car fortement basé sur les concepts d'événements et déclencheurs, mais aussi par ses capacités à intégrer de nouveaux types de données pris en compte par un optimiseur extensible. Postgres est devenu plus tard le SGBD Illustra racheté par Informix en 1995.
[Swami88] Swami A., Gupta A., « Optimization of Large Join Queries », ACM SIGMOD Intl. Conf., Chicago, 1988.
- Cet article étudie les stratégies de recherche du meilleur plan pour des requêtes comportant plus d'une dizaine de jointures. Des stratégies aléatoires telles que l'amélioration itérative et le recuit simulé sont comparées.
[TPC95] Transaction Processing Council, Benchmark TPC/D, San Fransisco, CA, 1995.
- La définition du TPC/D telle que proposée par le TPC.
[Ullman88] Ullman J.D., Principles of Database and Knowledge-base Systems, volumes I (631 pages) et II (400 pages), Computer Science Press, 1988.
- Deux volumes très complets sur les bases de données, avec une approche plutôt fondamentale. Jeffrey Ullman détaille tous les aspects des bases de données, depuis les méthodes d'accès aux modèles objet en passant par le modèle logique. Ces ouvrages sont finalement très centrés sur une approche par la logique aux bases de données. Les principaux algorithmes d'accès et d'optimisation de requêtes sont détaillés dans un chapitre plutôt formel.
[Valduriez84] Valduriez P., Gardarin G., « Join and Semi-Join Algorithms for a Multiprocessor Database Machine », ACM TODS, vol. 9, n° 1, 1984.
- Cet article introduit et compare différents algorithmes de jointure et semi-jointure pour machines multiprocesseurs. Il montre qu'aucune d'entre elles n'est dominante, mais que chacune a son domaine d'application selon la taille des relations et la sélectivité des jointures.
[Valduriez87] Valduriez P., « Join Indices », ACM TODS, vol. 12, n° 2, Juin 1987.
- L'auteur introduit les index de jointure, des index qui mémorisent la jointure précalculée entre deux tables. Chaque entrée de l'index est un couple de pointeurs référençant deux tuples participant à la jointure, l'un appartenant à la première table, l'autre à la seconde. De tels index sont très efficaces en interrogation. Le problème de ce type d'index est la mise à jour.
[Wong76] Wong E., Youssefi K., « Decomposition - A Strategy for Query Processing », ACM TODS, vol. 1, n° 3, Septembre 1976.
- Cet article présente la méthode de décomposition telle qu'implémentée dans le système Ingres. On a compris plus tard que la méthode permettait de détacher les semi-jointures en plus des sélections.