Cours complet pour apprendre les systèmes de gestion de bases de données

Le modèle relationnel est fondé sur la théorie mathématique bien connue des relations. Cette théorie se construit à partir de la théorie des ensembles. Trois notions sont importantes pour introduire les bases de données relationnelles. La première permet de définir les ensembles de départ. Ces ensembles sont les domaines de valeurs.

Les domaines sont donc les ensembles dans lesquels les données prennent valeur. Comme un ensemble, un domaine peut être défini en extension, en donnant la liste des valeurs composantes, ou en intention, en définissant une propriété caractéristique des valeurs du domaine. Au départ, les domaines ENTIER, REEL, BOOLEEN, CARACTERES (une chaîne de caractères de longueur fixe ou variable) sont définis en intention. À partir de ces domaines, il est possible de définir en intention des domaines plus spécifiques tels que MONNAIE (réel avec 2 chiffres derrière la virgule), DATE (entier de 6 chiffres jour, mois et an), TEMPS (heure en secondes), etc. Un domaine peut toujours être défini en extension, par exemple le domaine des couleurs de vins : COULEUR-VINS = {Rosé, Blanc, Rouge}.

Rappelons que le produit cartésien d'un ensemble de domaines D1, D2…, Dn est l'ensemble des vecteurs <v1, v2…, vn> où, pour i variant de 1 à n, vi est une valeur de Di. Par exemple, le produit cartésien des domaines COULEURVINS = {ROSE, BLANC, ROUGE} et CRUS = {VOLNAY, SANCERRE, CHABLIS} est composé des neuf vecteurs représentés figure VI.1.

COULEUR-VINS = {ROSE, BLANC, ROUGE}
CRUS = {VOLNAY, SANCERRE, CHABLIS}

Nous pouvons maintenant introduire la notion de relation, à la base du modèle.

Sous-ensemble d'un produit cartésien, une relation est composée de vecteurs. Une représentation commode d'une relation sous forme de table à deux dimensions a été retenue par Codd. Elle est généralement utilisée. Chaque ligne correspond à un vecteur alors que chaque colonne correspond à un domaine du produit cartésien considéré ; un même domaine peut bien sûr apparaître plusieurs fois. Par exemple, à partir des domaines COULEURS_VINS et CRUS, il est possible de composer la relation COULEURS_CRUS représentée sous forme tabulaire figure VI.2.

Pour pouvoir distinguer les colonnes d'une relation sans utiliser un index, et ainsi rendre leur ordre indifférent tout en permettant plusieurs colonnes de même domaine, il est nécessaire d'associer un nom à chaque colonne. Une colonne se distingue d'un domaine en ce qu'elle prend valeur dans un domaine et peut à un instant donné comporter seulement certaines valeurs du domaine. Par exemple, si le domaine est l'ensemble des entiers, seules quelques valeurs seront prises à un instant donné, par exemple {10, 20, 30}. L'ensemble des valeurs d'une colonne de relation est en général fini. Afin de bien distinguer domaine et colonne, on introduit la notion d'attribut comme suit :

Le nom associé à un attribut est souvent porteur de sens. Il est donc en général différent de celui du domaine qui supporte l'attribut. Ainsi, la première colonne de la relation COULEUR-CRUS pourra être appelée simplement COULEUR et la deuxième CRU. COULEUR et CRU seront donc deux attributs de la relation COULEUR-CRUS.

Les lignes d'une relation correspondent à des n-uplets de valeurs. Une ligne est aussi appelée tuple (du mot anglais tuple) : un tuple correspond en fait à un enregistrement dans une relation (encore appelée table).

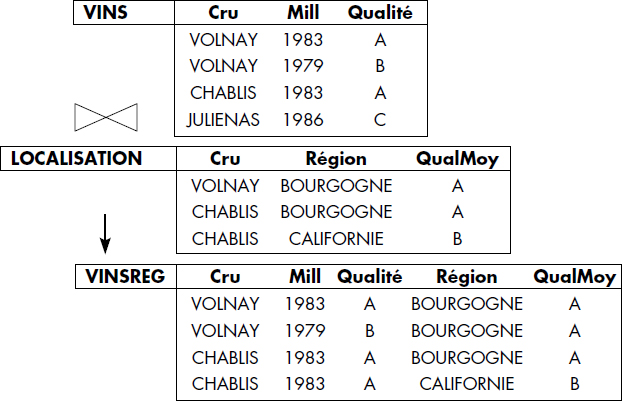
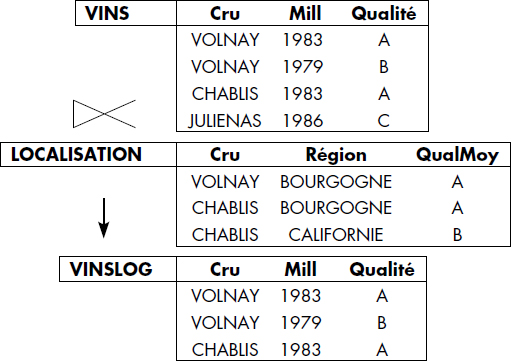
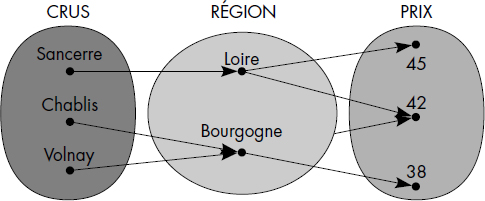
La notion de relation est bien connue en mathématiques : une relation naire est un ensemble de n-uplets. Un cas particulier souvent employé est la relation binaire, qui est un ensemble de paires ordonnées. Une relation naire est souvent représentée par un graphe entre les ensembles composants. Ainsi, la relation LOCALISATION, donnant la région de chaque cru et certains prix moyens des vins associés, est représentée par un graphe figure VI.3.

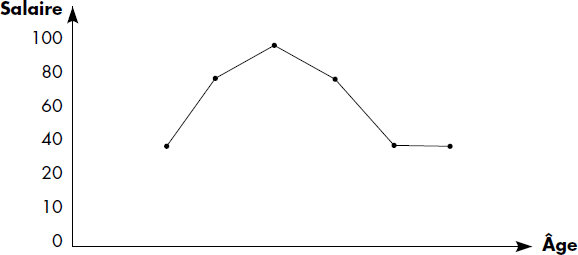
Une relation peut aussi être représentée sur un diagramme à n dimensions dont les coordonnées correspondent aux domaines participants. Ainsi, la relation STATISTIQUE, d'attributs AGE et SALAIRE, donnant la moyenne des salaires par âge, est représentée figure VI.4.

Une autre perception mathématique d'une relation consiste à voir chaque tuple t comme une fonction t : Ai -> Di pour i = 1, 2… n qui applique donc les attributs sur les domaines. Ainsi, une relation peut être vue comme un ensemble fini de fonctions. Bien sûr, cet ensemble varie en fonction du temps. Tout ceci montre la diversité des outils mathématiques qui peuvent être appliqués aux relations. En conséquence, le modèle relationnel peut apparaître comme un modèle mathématique simple des données. De plus, grâce à la représentation tabulaire, il est simple à appréhender pour les non-mathématiciens.

Comme tous les modèles de données, le modèle relationnel permet de décrire des données dont les valeurs varient en fonction du temps. Les relations varient en fonction du temps en ce sens que des tuples sont ajoutés, supprimés et modifiés dans une relation au cours de sa vie. Cependant, la structure d'une relation caractérisée par les trois concepts de domaine, relation et attribut est un invariant pour la relation (elle ne change pas en fonction du temps). Cette structure est capturée dans le schéma de la relation.

Un schéma de relation est noté sous la forme :

R (A1 : D1, A2 : D2…, Ai : Di… An : Dn)

R est le nom de la relation, Ai les attributs et Di les domaines associés. À titre d'exemple, la figure VI.5 propose deux schémas de relations : celui de la relation LOCALISATION introduite ci-dessus et celui de la relation VINS qui représente des vins caractérisés par un numéro, un cru, un millésime et un degré. Les domaines utilisés sont ceux des entiers, des réels et des chaînes de caractères de longueur variable (CHARVAR). La plupart du temps, lorsqu'on définit le schéma d'une relation, les domaines sont implicites et découlent du nom de l'attribut ; aussi omet-on de les préciser.

LOCALISATION (CRU : CHARVAR, REGION : CHARVAR, PRIX : FLOAT)
VINS (NV :INTEGER, CRU : CHARVAR, MILL :INTEGER, DEGRE : FLOAT)

Soulignons que le schéma d'une relation représente son intention, c'est-à-dire les propriétés (au moins certaines) communes et invariantes des tuples qu'elle va contenir au cours du temps. Au contraire, une table représente une extension d'une relation (voir figure VI.2 par exemple), c'est-à-dire une vue des tuples qu'elle contient à un instant donné. Une extension d'une relation R est aussi appelée instance de R. L'intention est le résultat de la description des données, alors qu'une extension (ou instance) fait suite à des manipulations et représente un état de la base.

Par définition, une relation est un ensemble de tuples. Un ensemble n'ayant pas d'élément en double, il ne peut exister deux fois le même tuple dans une relation. Afin d'identifier les tuples d'une relation sans donner toutes les valeurs et d'assurer simplement l'unicité des tuples, la notion de clé est utilisée.

De manière plus formelle, une clé d'une relation R est un ensemble d'attributs K tel que, quels que soient les tuples t1 et t2 d'une instance de R, t1(K) ≠ t2(K), c'est-à-dire que t1 et t2 ont des valeurs de K différentes. Un ensemble d'attributs contenant une clé est appelé super-clé [Ullman88].

Toute relation possède au moins une clé, car la connaissance de tous les attributs permet d'identifier un tuple unique. S'il existe plusieurs clés, on en choisit en général une arbitrairement qui est appelée clé primaire. Par exemple, NV peut constituer une clé primaire pour la relation VINS. Le couple <CRU,MILLESIME> est une clé alternative.

Soulignons que la notion de clé caractérise l'intention d'une relation : dans toute extension possible d'une relation, il ne peut exister deux tuples ayant même valeur pour les attributs clés. La détermination d'une clé pour une relation nécessite donc une réflexion sur la sémantique de la relation, c'est-à-dire sur toutes les extensions possibles et non pas sur une extension particulière.

Le modèle relationnel est souvent utilisé pour représenter des entités du monde réel qui sont les objets ayant une existence propre, et des associations entre ces objets [Chen76]. Une entité correspond alors à un tuple dans une relation qui comporte à la fois la clé de l'entité et ses caractéristiques sous forme d'attributs. Une entité est identifiée par la valeur de sa clé. Un type d'association est modélisé par une relation comportant les clés des entités participantes ainsi que les caractéristiques propres à l'association.

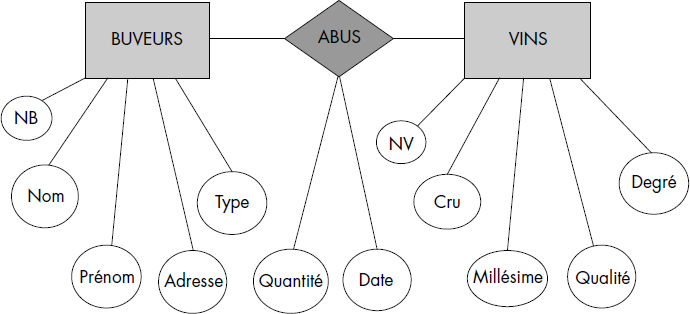
À titre d'exemple, nous considérons les entités BUVEURS et VINS du monde réel : la clé de l'entité BUVEURS est le numéro de buveur NB et celles de l'entité VINS le numéro de vin NV. Ces entités peuvent être associées par une consommation d'un vin par un buveur : une consommation sera par exemple modélisée par une association ABUS entre le buveur et le vin. Cette base typique et simple, qui servira souvent d'exemple, est appelée DEGUSTATION. Le diagramme entité-association de cette base est représenté figure VI.6.

En relationnel, chaque entité est représentée par une table. Une association est aussi représentée par une table, dont les attributs seront les clés des entités participantes, c'est-à-dire NB et NV, ainsi que les attributs caractérisant l'association, par exemple la date et la quantité bue. On aboutit ainsi au schéma relationnel représenté figure VI.7.

BUVEURS (NB, NOM, PRENOM, ADRESSE, TYPE)
VINS (NV, CRU, MILL QUALITE, DEGRE)
ABUS (NB, NV, DATE, QUANTITE)

L'utilisation du modèle relationnel pour représenter des entités et des associations ne permet pas jusque-là de représenter le fait que l'association entre une consommation et un vin est obligatoire, c'est-à-dire que tout abus doit correspondre à un vin existant dans la base. De même, le fait que le lien entre une consommation et un buveur soit obligatoire est perdu. Le maintien de liens obligatoires a justifié l'introduction de la notion de contrainte référentielle [Date81].

Une telle contrainte d'intégrité s'applique en général aux associations obligatoires : une telle association ne peut exister que si les entités participant à l'association existent déjà. Notez que dans la définition, R1 et R2 ne sont pas forcément distinctes : l'association peut en effet porter sur deux entités de même type, par exemple entre une personne et ses parents.

La représentation de contraintes de référence peut s'effectuer par la définition de clés étrangères dans une relation : une clé étrangère est un groupe d'attributs qui doit apparaître comme clé dans une (autre) relation. Par exemple, la relation ABUS (NB, NV, DATE, QUANTITE) a pour clé <NB, NV, DATE> et a deux clés étrangères, NB dans BUVEURS et NV dans VINS.

Les contraintes référentielles définissent des liens obligatoires entre relations. Ce sont des contraintes très fortes qui conditionnent le succès des opérations de mises à jour. Lors de l'insertion d'un tuple dans une relation référençante, il faut vérifier que les valeurs de clés étrangères existent dans les relations référencées. Par exemple, lors de l'insertion d'un abus, il faut que le vin et le buveur associés existent, sinon l'insertion est refusée pour cause de violation d'intégrité. Lors de la suppression d'un tuple dans une relation référencée, il faut vérifier qu'aucun tuple n'existe dans chaque relation référençante ; s'il en existe, le système peut soit refuser la suppression, soit la répercuter en cascade (c'est-à-dire, supprimer les tuples référençants). Par exemple, la suppression d'un vin entraînera la vérification qu'aucun abus ne référence ce vin. Les contraintes d'intégrité référentielles sont donc des liens forts qui rendent les relations dépendantes ; en quelque sorte, elles introduisent des liens hiérarchiques depuis les relations référencées vers les relations référençantes.

Lors de l'insertion de tuples dans une relation, il arrive fréquemment qu'un attribut soit inconnu ou non applicable ; par exemple, la quantité de vin bu par un buveur à une certaine date peut être inconnue ; si un vin ne possède pas de millésime, l'attribut millésime est inapplicable à ce vin. On est alors amené à introduire dans la relation une valeur conventionnelle, appelée valeur nulle.

La signification précise d'une valeur nulle est souvent ambiguë ; le groupe ANSI/X3/SPARC a recensé quatorze significations possibles, parmi lesquelles valeur inconnue et valeur inapplicable sont les plus caractéristiques.

Tout attribut dans une relation ne peut prendre une valeur nulle ; en effet, l'existence d'une clé unique impose la connaissance de la clé afin de pouvoir vérifier que cette valeur de clé n'existe pas déjà. Ainsi, une contrainte structurelle du modèle relationnel est la contrainte d'entité définie ci-dessous [Date81].

À moins qu'il n'en soit spécifié autrement par une contrainte sémantique, le modèle relationnel n'impose pas que les clés étrangères qui n'appartiennent pas à une clé primaire soient non nulles. Cela peut permettre une certaine souplesse, par exemple d'enregistrer des employés qui ne sont attachés à aucun service.

En théorie, une relation est construite à partir d'un ensemble de domaines. En pratique, les domaines gérés par les systèmes sont souvent limités aux types de base entier, réel, chaîne de caractères, parfois monnaie et date. Afin de spécialiser un type de données pour composer un domaine plus fin (par exemple, le domaine des salaires mensuels qui sont des réels compris entre 6 000 et 1 000 000 de francs), la notion de contrainte de domaine est souvent ajoutée aux règles d'intégrité structurelle du relationnel. Cette notion peut être introduite comme suit :

L'assertion logique est l'appartenance à une plage de valeurs ou à une liste de valeurs. Par exemple, SALAIRE ≥ 5 000 et ≤ 1 000 000, COULEUR ∈ {BLEU, BLANC, ROUGE}, etc. Les contraintes permettent de contrôler la validité des valeurs introduites lors des insertions ou mises à jour. La non-nullité d'une colonne peut aussi être considérée comme une contrainte de domaine, par exemple DEGRE IS NULL.

XI-4-1-1. Union▲

L'union est l'opération classique de la théorie des ensembles adaptée aux relations de même schéma.

Notion VI.11 : Union (Union)

Opération portant sur deux relations de même schéma RELATION1 et RELATION2 consistant à construire une relation de même schéma RELATION3 ayant pour tuples ceux appartenant à RELATION1 ou RELATION2 ou aux deux relations.

Plusieurs notations ont été introduites pour cette opération, selon les auteurs :

• RELATION1 ∪ RELATION2
• UNION (RELATION1, RELATION2)
• APPEND (RELATION1, RELATION2)

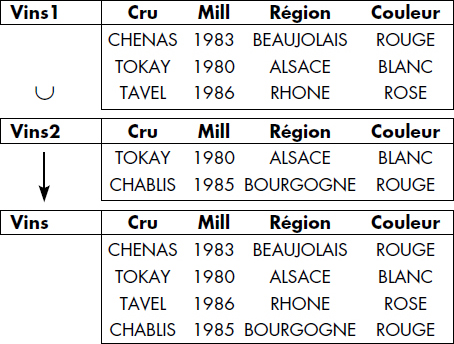
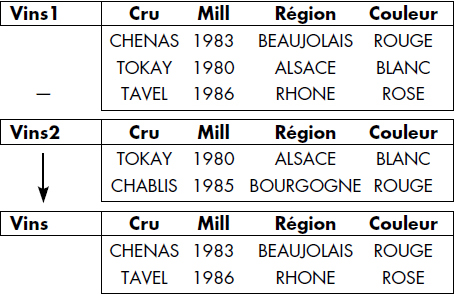
La notation graphique représentée figure VI.8 est aussi utilisée. À titre d'exemple, l'union des relations VINS1 et VINS2 est représentée figure VI.9.

XI-4-1-2. Différence▲

La différence est également l'opération classique de la théorie des ensembles adaptée aux relations de même schéma.

Notion VI.12 : Différence (Difference)

Opération portant sur deux relations de même schéma RELATION1 et RELATION2, consistant à construire une relation de même schéma RELATION3 ayant pour tuples ceux appartenant à RELATION1 et n'appartenant pas à RELATION2.

La différence est un opérateur non commutatif : l'ordre des relations opérandes est donc important. Plusieurs notations ont été introduites pour cette opération, selon les auteurs :

• RELATION1 - RELATION2
• DIFFERENCE (RELATION1, RELATION2)
• REMOVE (RELATION1, RELATION2
• MINUS (RELATION1, RELATION2)

La notation graphique représentée figure VI.10 est aussi utilisée. À titre d'exemple, la différence des relations VINS1 - VINS2 est représentée figure VI.11.

XI-4-1-3. Produit cartésien▲

Le produit cartésien est l'opération ensembliste que nous avons rappelée ci-dessus pour définir le concept de relations. Elle est adaptée aux relations. Cette fois, les deux relations n'ont pas nécessité d'avoir même schéma.

Notion VI.13 : Produit cartésien (Cartesian product)

Opération portant sur deux relations RELATION1 et RELATION2, consistant à construire une relation RELATION3 ayant pour schéma la concaténation de ceux des relations opérandes et pour tuples toutes les combinaisons des tuples des relations opérandes.

Des notations possibles pour cette opération sont :

• RELATION1 X RELATION2
• PRODUCT (RELATION1, RELATION2)
• TIMES (RELATION1, RELATION2)

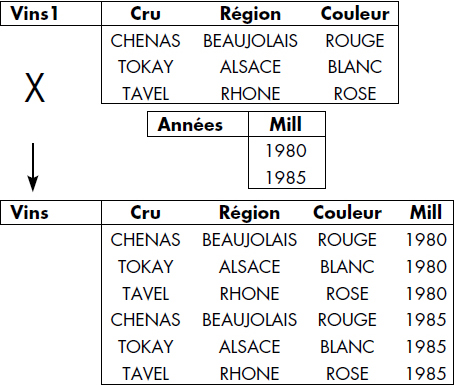
La notation graphique représentée figure VI.12 est aussi utilisée. À titre d'exemple, la relation VINS représentée figure VI.13 est le produit cartésien des deux relations CRUS et ANNEES de la même figure.

XI-4-2-1. Projection▲

La projection est une opération spécifique aux relations qui permet de supprimer des attributs d'une relation. Son nom provient du fait qu'elle permet de passer d'une relation n-aire à une relation p-aire avec p<n, donc d'un espace à n dimensions à un espace à moins de dimensions.

Notion VI.14 : Projection (Projection)

Opération sur une relation RELATION1 consistant à composer une relation RELATION2 en enlevant à la relation initiale tous les attributs non mentionnés en opérandes (aussi bien au niveau du schéma que des tuples) et en éliminant les tuples en double qui sont conservés une seule fois.

Les notations suivantes sont utilisées pour cette opération, en désignant par Attributi, Attributj… Attributm les attributs de projection :

• ????Attributi, Attributj… Attributm (RELATION1)
• RELATION1 [Attributi, Attributj… Attributm]
• PROJECT (RELATION1, Attributi, Attributj… Attributm)

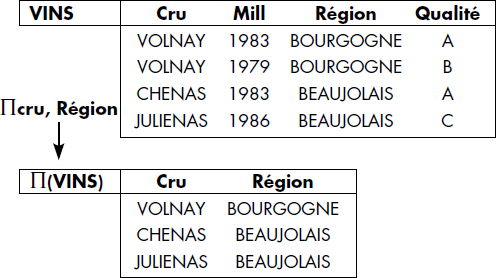
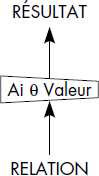
La notation graphique représentée figure VI.14 est aussi utilisée. Le trapèze horizontal signifie que l'on réduit le nombre de colonnes de la relation : partant du nombre représenté par la base, on passe au nombre représenté par l'antibase. La figure VI.15 donne un exemple de projection d'une relation VINS comportant aussi l'attribut QUALITE sur les attributs MILLESIME et QUALITE.

XI-4-2-2. Restriction▲

La restriction est aussi une opération spécifique unaire, qui produit une nouvelle relation en enlevant des tuples à la relation opérande selon un critère.

Notion VI.15 : Restriction (Restriction)

Opération sur une relation RELATION1 produisant une relation RELATION2 de même schéma, mais comportant les seuls tuples qui vérifient la condition précisée en argument.

Les conditions possibles sont du type :

 

Sélectionnez

<Attribut> <Opérateur> <Valeur>

où l'opérateur est un opérateur de comparaison choisi parmi {=,<, ≤, ≥, >, ≠}. L'attribut doit appartenir à la relation sur laquelle s'applique le critère. Par exemple, pour la relation VINS, CRU = "Chablis" est une condition de restriction possible. DEGRE > 12 est une autre condition possible. Il est aussi possible d'utiliser des compositions logiques de critères simples, c'est-à-dire des « et » et « ou » de conditions élémentaires. On pourra par exemple utiliser le critère CRU = "Chablis" et DEGRE > 12, ou encore le critère CRU = "Chablis" ou DEGRE = 12. Toute composition de critères valides par conjonction et disjonction (des parenthèses peuvent être utilisées pour préciser les priorités) est valide. Notons que les compositions logiques peuvent aussi être obtenues par union et intersection de relations restreintes (voir ci-dessous).

Les notations suivantes sont utilisées pour la restriction :

• σ_condition (RELATION1)
• RELATION1 [Condition]
• RESTRICT (RELATION1, Condition)

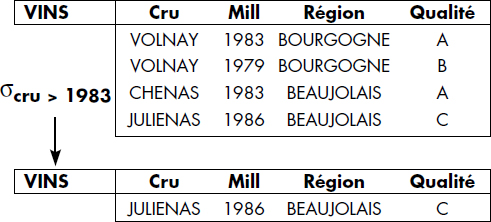
ainsi que la notation graphique représentée figure VI.16. Le trapèze vertical signifie que l'on réduit le nombre de tuples de la relation : partant du nombre représenté par le côté gauche, on passe au nombre représenté par le côté droit. La figure VI.17 représente la restriction d'une relation VINS enrichie d'un attribut QUALITE par la condition QUALITE = "BONNE".

XI-4-2-3. Jointure▲

La jointure est une des opérations essentielles de l'algèbre relationnelle, sans doute la plus difficile à réaliser dans les systèmes. La jointure permet de composer deux relations à l'aide d'un critère de jointure. Elle peut être vue comme une extension du produit cartésien avec une condition permettant de comparer des attributs. Nous la définirons comme suit :

Notion VI.16 : Jointure (Join)

Opération consistant à rapprocher selon une condition les tuples de deux relations RELATION1 et RELATION2 afin de former une troisième relation RELATION3 qui contient l'ensemble de tous les tuples obtenus en concaténant un tuple de RELATION1 et un tuple de RELATION2 vérifiant la condition de rapprochement.

La jointure de deux relations produit donc une troisième relation qui contient toutes les combinaisons de tuples des deux relations initiales satisfaisant la condition spécifiée. La condition doit bien sûr permettre le rapprochement des deux relations, et donc être du type :

 

Sélectionnez

<Attribut1> <opérateur> <Attribut2>

où Attribut1 appartient à RELATION1 et Attribut2 à RELATION2. Selon le type d'opérateur, on distingue :

• l'équi-jointure dans le cas où l'opérateur est =, qui est une véritable composition de relations au sens mathématique du terme ;
• l'inéqui-jointure dans les autres cas, c'est-à-dire avec un des opérateurs <, ≤, >, ≥, ≠.

Dans le cas d'équi-jointure, les deux attributs égaux apparaissent chacun dans le résultat : il y a donc duplication d'une même valeur dans chaque tuple. Afin d'éliminer cette redondance, on définit la jointure naturelle comme suit :

Notion VI.17 : Jointure naturelle (Natural join)

Opération consistant à rapprocher les tuples de deux relations RELATION1 et RELATION2 afin de former une troisième relation RELATION3 dont les attributs sont l'union des attributs de RELATION1 et RELATION2, et dont les tuples sont obtenus en composant un tuple de RELATION1 et un tuple de RELATION2 ayant même valeur pour les attributs de même nom.

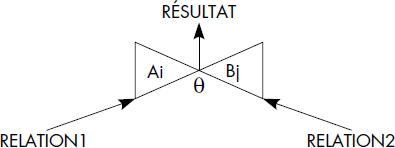
L'opération de jointure est représentée par l'une des notations suivantes, la condition étant simplement omise dans le cas de jointure naturelle (c'est alors l'égalité des attributs de même nom) :

• RELATION1 RELATION2
  Condition
• JOIN (RELATION1, RELATION2, Condition)

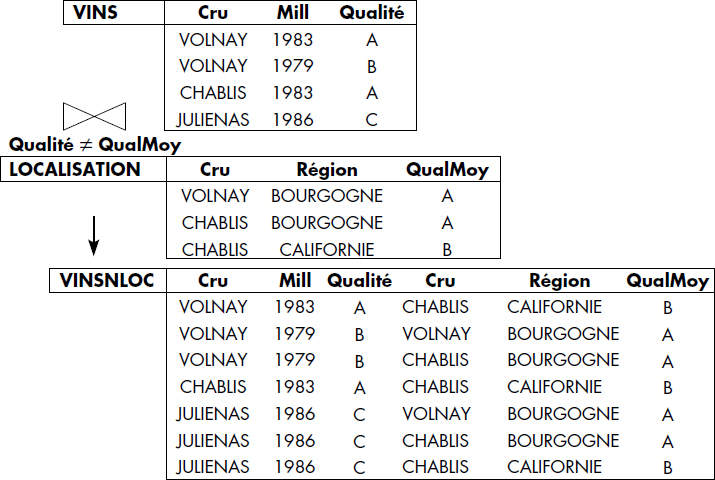
La figure VI.18 donne la représentation graphique de l'opération de jointure ; la figure VI.19 illustre cette opération en effectuant la jointure naturelle des deux relations VINS et LOCALISATION. L'inéqui-jointure de ces deux relations selon la condition QUALITE > QUALITE MOYENNE est représentée figure VI.20. On suppose que les qualités sont codées par ordre décroissant A, B, C, D, E.

La jointure n'est pas toujours considérée comme une opération de base de l'algèbre relationnelle. En effet, si l'on étend la définition de la restriction de manière à considérer des conditions multiattributs du type <Attribut1> <Opérateur> <Attribut2>, alors la jointure peut être obtenue par un produit cartésien suivi d'une restriction du résultat comme suit :

 

Sélectionnez

JOIN (RELATION1, RELATION2, Condition) =
RESTRICT ((RELATION1 X RELATION2), Condition)

Compte tenu de son importance, nous avons préféré ici définir la jointure comme une opération de base.

L'intersection est l'opération classique de la théorie des ensembles adaptée aux relations de même schéma.

Plusieurs notations ont été introduites pour cette opération selon les auteurs :

• RELATION1 ∩ RELATION2
• INTERSECT (RELATION1, RELATION2)
• AND (RELATION1, RELATION2)

La notation graphique représentée figure VI.21 est aussi utilisée.

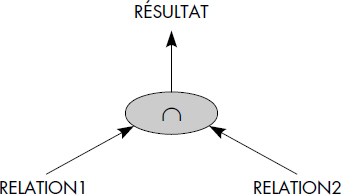
L'intersection est une opération redondante avec les opérations de base, puisqu'il est possible de l'obtenir à partir de la différence à l'aide d'une des formules suivantes :

RELATION1 ∩ RELATION2 = RELATION1 - (RELATION1 - RELATION2)
RELATION1 ∩ RELATION2 = RELATION2 - (RELATION2 - RELATION1)

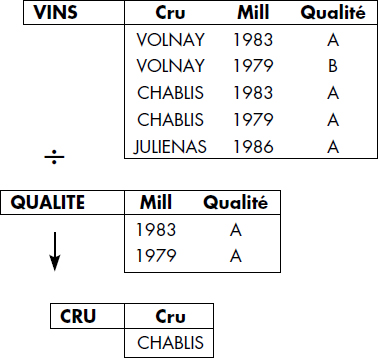
La division permet de rechercher dans une relation les sous-tuples qui sont complétés par tous ceux d'une autre relation. Elle permet ainsi d'élaborer la réponse à des questions de la forme « quel que soit x, trouver y » de manière simple.

De manière plus formelle, désignons par ai une valeur quelconque de l'attribut Ai. Un tuple est alors une suite de valeurs <a1, a2, a3…>. Utilisant ces notations, le quotient de D par D est défini par :

Q = {<a1, a2… ap> tel-que quel-que-soit <ap+1… an> de d,
<a1, a2… ap, ap+1…, an> appartient à D}

Les notations possibles pour la division sont :

• D ÷ d
• DIVISION (D, d)

ainsi que la représentation graphique de la figure VI.22. Un exemple de division est représenté figure VI.23.

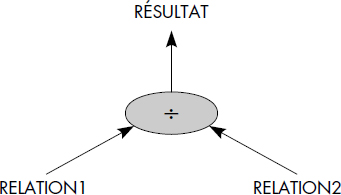
La division peut être obtenue à partir de la différence, du produit cartésien et de la projection comme suit :

• D - d = R1 - R2 avec
• R1 = ????A1, A2… Ap(D)
• R2 = ????A1, A2… Ap ((R1 X d) - D)

Le complément permet de trouver les tuples qui n'appartiennent pas à une relation. Il suppose a priori que les domaines sont finis (sinon on obtient des relations infinies).

Le complément d'une relation RELATION1 est noté au choix :

• RELATION1
• NOT(RELATION1)
• COMP(RELATION1)

La figure VI.24 illustre cette opération dans un cas simple. C'est une opération peu utilisée du fait qu'elle permet de générer des tuples qui ne sont pas dans la base, en général très nombreux. Si l'on note par X Di le produit cartésien des domaines, le complément d'une relation RELATION1 est obtenu à partir de la différence comme suit :

• NOT (RELATION1) = X Di - RELATION1

L'éclatement [Fagin80] est une opération qui n'appartient pas vraiment à l'algèbre rationnelle puisqu'elle donne deux relations en résultats, à partir d'une. Elle est cependant utile pour partitionner une relation horizontalement en deux sous-relations. À ce titre, elle est considérée comme une extension de l'algèbre.

Cet opérateur appliqué à la relation RELATION1 génère donc deux relations R1 et R2 qui seraient obtenues par restriction comme suit :

• R1 = RESTRICT (RELATION1, ¬Condition)
• R2 = RESTRICT (RELATION1, Condition)

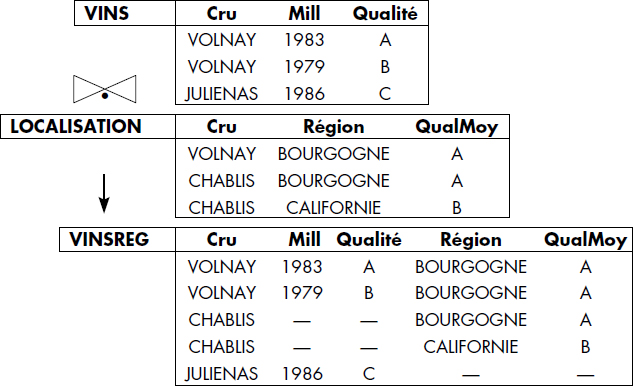
Les jointures définies ci-dessus perdent des tuples d'au moins une relation quand les relations jointes n'ont pas de projections identiques sur l'attribut de jointure. Pour préserver toutes les informations dans tous les cas, il est nécessaire de définir des jointures qui conservent les tuples sans correspondants avec des valeurs nulles associées quand nécessaire. C'est dans ce but que Codd [Codd79] a introduit les jointures externes.

Cette opération est très utile, en particulier pour composer des vues sans perte d'informations. Elle se note en général comme suit :

• RELATION1 RELATION2
• EXT-JOIN (RELATION1, RELATION2)

La jointure externe permet par exemple de joindre des tables CLIENTS et COMMANDES sur un numéro de client commun, en gardant les clients sans commande et les commandes sans client associé. Elle est donc très utile en pratique. On peut aussi distinguer la jointure externe droite qui garde seulement les tuples sans correspondant de la relation de droite. On notera celle-ci ou REXT-JOIN. De même, on peut distinguer la jointure externe gauche ( ou LEXT-JOIN). Un exemple de jointure externe complète apparaît figure VI.25.

Dans certains cas, lors de l'exécution d'une jointure, il n'est pas nécessaire de conserver tous les attributs des deux relations en résultat : seuls les attributs d'une des deux relations sont conservés. Une opération spécifique de semi-jointure, très utile pour optimiser l'évaluation des questions, a été définie [Berstein81].

La semi-jointure de la relation RELATION1 par la relation RELATION2 est notée :

• RELATION1 RELATION2
• SEMI-JOIN (RELATION1, RELATION2)

Elle est équivalente à la jointure des relations RELATION1 et RELATION2 suivie par une projection du résultat sur les attributs de la relation RELATION1. Notez que l'opération n'est pas symétrique puisque seuls des tuples de la première relation sont conservés. Elle peut être vue comme une restriction de la relation RELATION1 par les valeurs des attributs de jointure figurant dans la relation RELATION2. La figure VI.26 illustre cette opération de semi-jointure.

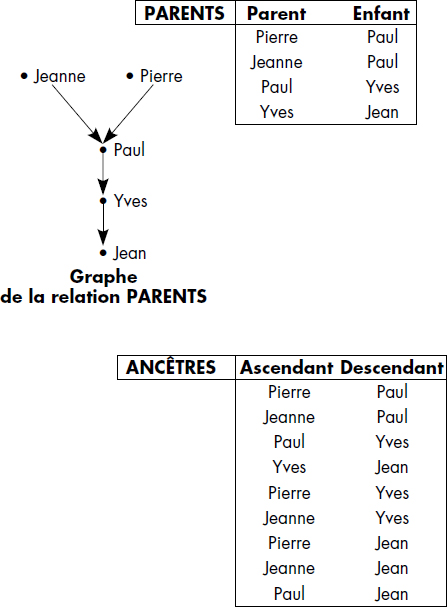
La fermeture transitive est une opération très particulière qui permet d'ajouter des tuples à une relation. Elle n'appartient pas à l'algèbre rationnelle, mais peut être vue comme une de ses extensions. Il n'est pas possible de constituer cette opération avec un nombre fixe d'opérations de l'algèbre rationnelle : elle peut être effectuée par une série de jointures/projections/unions, mais le nombre d'opérations à effectuer dépend du contenu de la relation. Certains auteurs considèrent que c'est une faiblesse de l'algèbre relationnelle que de ne pas pouvoir exprimer une fermeture transitive par une expression constante d'opérations élémentaires.

Cette opération se note suivant les auteurs :

• τ(R)
• R+
• CLOSE(R)

Pour effectuer une fermeture transitive, il est nécessaire d'effectuer une boucle d'opérations jusqu'à obtention de la fermeture complète. On doit donc utiliser un langage de programmation avec une boucle while, comme suit :

• τ(R) = while τ(R) change do τ(R)
•       = τ(R) ∪ ????A1,A4 (R τ(R)).

Cette opération permet par exemple de calculer à partir d'une relation PARENTS (Parent, Enfant) la relation ANCETRES (Ascendant, Descendant), qui donne toute la filiation connue d'une personne. La figure VI.27 illustre cette opération. La fermeture transitive de PARENTS est calculée par jointures/projections/unions successives de la relation PARENTS avec elle-même jusqu'à saturation, c'est-à-dire jusqu'à obtention d'une relation stable à laquelle une nouvelle jointure/projection/union n'apporte plus de tuples. On voit que la relation ANCETRES représente le graphe correspondant à la fermeture transitive du graphe de la relation PARENTS.

En utilisant des expressions d'opérations de l'algèbre relationnelle, il est possible d'élaborer les réponses à la plupart des questions que l'on peut poser à une base de données relationnelle. Plus précisément, les opérations de base de l'algèbre relationnelle constituent un langage complet, c'est-à-dire ayant la puissance de la logique du premier ordre.

Nous avons étudié plus précisément la logique du premier ordre et les langages d'interrogation qui en découlent au chapitre V. Disons simplement que l'algèbre relationnelle permet d'exprimer toute question exprimable avec la logique du premier ordre sans fonction, par exemple avec le calcul de tuple ou de domaine. L'algèbre relationnelle peut d'ailleurs être étendue avec des fonctions [Zaniolo85].

Voici quelques questions sur la base DEGUSTATION dont le schéma a été représenté figure VI.7. Elles peuvent être exprimées comme des expressions d'opérations, ou comme des opérations successives appliquées sur des relations intermédiaires ou de base, générant des relations intermédiaires. Pour des raisons de clarté, nous avons choisi cette deuxième représentation. L'expression peut être obtenue simplement en supprimant les relations intermédiaires notées Ri.

• (Q1) Donner les degrés des vins de crus Morgon et de millésime 1978 :

   

  Sélectionnez

  R1 = RESTRICT (VINS, CRUS = "MORGON")
  R2 = RESTRICT (VINS, MILLESIME = 1978)
  R3 = INTERSECT (R1, R2)
  RESULTAT = PROJECT (R3, DEGRE)

• (Q2) Donner les noms et prénoms des buveurs de Morgon ou Chenas :

   

  Sélectionnez

  R1 = RESTRICT (VINS, CRU = "MORGON")
  R2 = RESTRICT(VINS, CRUS = "CHENAS")
  R3 = UNION (R1, R2)
  R4 = JOIN (R3, ABUS)
  R5 = JOIN (R4, BUVEURS)
  RESULTAT = PROJECT (R5, NOM, PRENOM)

• (Q3) Donner les noms et adresses des buveurs ayant bu plus de 10 bouteilles de Chablis 1976 avec le degré de ce vin :

   

  Sélectionnez

  R1 = RESTRICT (ABUS, QUANTITE > 10)
  R2 = RESTRICT (VINS, CRU = "CHABLIS")
  R3 = RESTRICT (VINS, MILLESIME = 1976)
  R4 = INTERSECT (R2, R3)
  R5 = JOIN (R1, R4)
  R6 = PROJECT (R5, NB, DEGRE)
  R7 = JOIN (R6, BUVEURS)
  RESULTAT = PROJECT (R7, NOM, ADRESSE, DEGRE)

• (Q4) Donner les noms des buveurs n'ayant bu que du Morgon :

R1 = JOIN(BUVEURS,ABUS,VINS)
R2 = RESTRICT(R1, CRU = "Morgon")
R3 = PROJECT(R2, NOM)
R4 = RESTRICT(R1, CRU ≠ "Morgon")
R5 = PROJECT(R1, NOM)1
RESULTAT = MINUS(R3 - R5)

Si l'on accepte les relations constantes, l'algèbre relationnelle permet aussi d'exécuter les mises à jour. Par exemple, l'intersection du vin [100, TOKAY, 1978, 13] s'effectuera comme suit :

R1 = CONSTANTE (VINS, [100, TOKAY, 1978, 13])
VINS = UNION (VINS, R1)

où CONSTANTE permet de définir une relation de même schéma que la relation VINS contenant le seul tuple indiqué en argument.

Une question exprimée sous forme d'un programme d'opérations de l'algèbre relationnelle peut être représentée par un arbre relationnel. Les nœuds correspondent aux représentations graphiques des opérations indiquées ci-dessus et les arcs aux flots de données entre opérations.

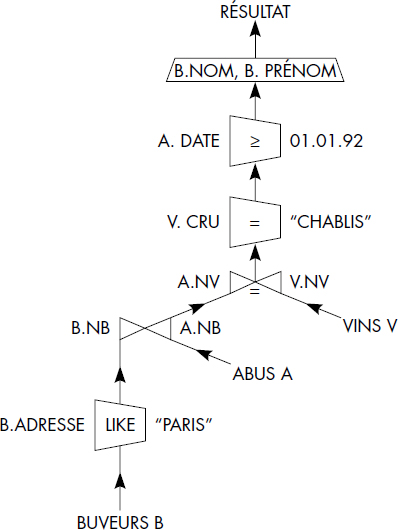
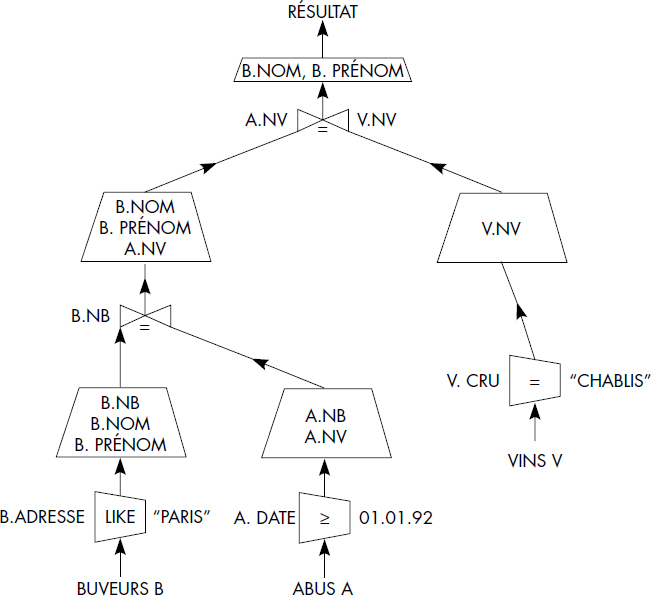
Ainsi, la question « Noms et Prénoms des buveurs habitant Paris ayant bu du Chablis depuis le 1^er janvier 1992 » peut être exprimée à l'aide de l'arbre représenté figure VI.28. Plusieurs arbres équivalents peuvent être déduits d'un arbre donné à l'aide de règles de transformation simples, telles que la permutation des jointures et restrictions, la permutation des projections et des jointures, le regroupement des intersections sur une même relation, etc. Ces transformations sont à la base des techniques d'optimisation de questions qui dépassent le sujet de ce chapitre. La figure VI.29 propose un arbre équivalent à celui de la figure VI.28, obtenu par descente de projections et regroupement d'intersections.

La composition d'opérations de l'algèbre relationnelle ne nécessite pas toujours d'attendre le résultat de l'opération précédente pour exécuter l'opération suivante. Restriction, projection et jointure peuvent ainsi être exécutées par des algorithmes à flots de données. Des opérateurs se succédant sur un arbre peuvent donc être exécutés en parallèle par des algorithmes « pipe-line ». Des opérateurs figurant sur des branches distinctes d'un arbre peuvent aussi être exécutés en parallèle de manière indépendante. La représentation par arbre algébrique met ainsi en évidence les possibilités de parallélisme et les enchaînements nécessaires. Ces propriétés des arbres relationnels sont importantes pour optimiser les questions dans des contextes parallèles.

La possibilité d'effectuer des calculs sur les attributs est simplement introduite en généralisant projection, restriction et jointure par introduction de fonctions. Ainsi, tout attribut apparaissant en argument d'une opération est remplacé par une expression d'attributs.

Voici des exemples d'expressions d'attributs :

10 + 50 - 23 ;
QUANTITE * 50 ;
QUANTITE * DEGRE / 100 ;
QUANTITE - QUANTITE * DEGRE / 100.

De telles expressions peuvent donc être utilisées comme arguments de projections, de restrictions, voire de jointures. Le programme d'algèbre relationnelle suivant illustre ces possibilités :

R1 = JOIN (VINS, ABUS, DEGRE*QUANTITE/100 > QUANTITE/10)
R2 = RESTRICT(R1, DEGRE*QUANTITE/100 > 10)
RESULTAT = PROJECT(R2, CRU, QUANTITE - QUANTITE*DEGRE/100)

La notion d'expression d'attributs peut être généralisée avec des fonctions autres que les fonctions arithmétiques, par exemple des fonctions écrites dans un langage externe. On aboutit ainsi à une généralisation de l'algèbre relationnelle aux fonctions [Zaniolo85].

Les expressions d'attributs permettent d'effectuer des opérations de calcul en ligne, sur des attributs de relations. En pratique, il est nécessaire d'effectuer des opérations de calcul en colonnes, sur des tuples de relations, cela par exemple afin de sommer des dépenses, etc. Le concept d'agrégat permet de telles opérations.

Les fonctions de calcul sur ensemble les plus souvent proposées sont :

• SOMME (SUM) permettant de calculer la somme des éléments d'un ensemble ;
• MOYENNE (AVG) permettant de calculer la moyenne des éléments d'un ensemble ;
• MINIMUM (MIN) permettant de sélectionner l'élément minimum d'un ensemble ;
• MAXIMUM (MAX) permettant de sélectionner l'élément maximum d'un ensemble ;
• COMPTE (COUNT) permettant de compter les éléments d'un ensemble.

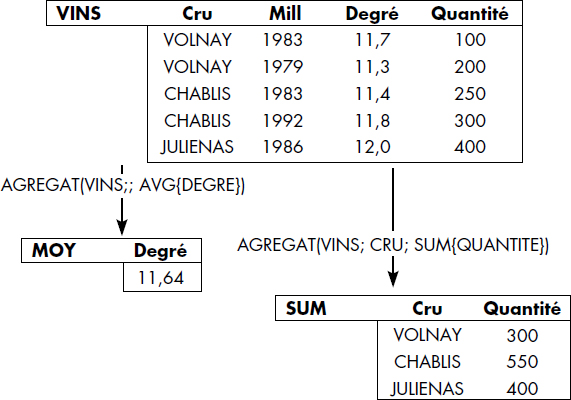
La figure VI.30 illustre le concept d'agrégat. La table VINS est enrichie d'un attribut QUANTITE. L'agrégat représenté calcule la somme des quantités par CRU. L'opération générique s'écrit :

R = AGREGAT(<RELATION> ; <ATTRIBUT1> ; <FONCTION>{<ATTRIBUT2>})

<Attribut1> représente un ou plusieurs attributs utilisés pour le partitionnement. Fonction est la fonction d'ensemble appliquée à l'attribut <Attribut2>. Par exemple, on écrit :

RESULTAT = AGREGAT(VINS ; CRU ; SUM{QUANTITE})

pour l'agrégat illustré figure VI.30figure VI.30. Notez qu'un agrégat peut s'effectuer sans partitionnement ; on peut par exemple calculer simplement la moyenne de tous les degrés comme indiqué par la commande :

RESULTAT = AGREGAT(VINS ; ; AVG{DEGRE}).