Cours complet pour apprendre les systèmes de gestion de bases de données

Rappelons que la logique du premier ordre, aussi appelée calcul de prédicats, est un langage formel utilisé pour représenter des relations entre objets et pour déduire de nouvelles relations à partir de relations connues comme vraies. Elle peut être vue comme un formalisme utilisé pour traduire des phrases et déduire de nouvelles phrases à partir de phrases connues.

La logique du premier ordre repose sur un alphabet qui utilise les symboles suivants :

1. Des variables généralement notées x, y, z …
2. Des constantes généralement notées a, b, c …
3. Des prédicats généralement notés P, Q, R …, chaque prédicat pouvant recevoir un nombre fixe d'arguments (n pour un prédicat naire).
4. Les connecteurs logiques ∧, ∨, ⇒, ¬.
5. Des fonctions généralement dénotées f, g, h…, chaque fonction pouvant recevoir un nombre fixe d'arguments (n pour une fonction naire).
6. Les quantificateurs ∀ et ∃.

Des règles syntaxiques simples permettent de construire des formules. Un terme est défini récursivement comme une variable ou une constante ou le résultat de l'application d'une fonction à un terme. Par exemple, x, a, f(x) et f(f(x)) sont des termes. Une formule est une phrase bien construite du langage. Une formule est définie comme suit :

1. Si P est un prédicat à n arguments (n places) et t1, t2…tn des termes, alors P(t1,t2… tn) est une formule atomique.
2. Si F1 et F2 sont des formules, alors F1 ∧ F2, F1 ∨ F2, F1 ⇒ F2 et ¬ F1 sont des formules.
3. Si F est une formule et x une variable non quantifiée (on dit aussi libre) dans F, alors ∀x F et ∃x F sont des formules.

Nous résumons ci-dessous les concepts essentiels introduits jusque-là sous forme de notions.

Pour indiquer les priorités entre connecteurs logiques, il est possible d'utiliser les parenthèses : si F est une formule valide, (F) en est aussi une. Afin d'éviter les parenthèses dans certains cas simples, nous supposerons une priorité des opérateurs logiques dans l'ordre descendant ¬, ∨, ∧, et ⇒. Voici quelques exemples de formules formelles :

P(a,x) ∧ Q(x,y),
¬ Q(x,y),
∀x ∃y (Q(x,y) ∨ P(a,x)),
∀x (R(x) ∧ Q(x,a) ⇒ P(b,f(x))).

Afin de donner des exemples plus lisibles de formules, nous choisirons un vocabulaire moins formel, les prédicats et fonctions étant des noms ou des verbes du langage courant et les constantes des chaînes de caractères désignant par exemple des services ou des employés. Voici quelques exemples de formules proches du langage naturel :

Une formule peut être interprétée comme une phrase sur un ensemble d'objets : il est possible de lui donner une signification vis-à-vis de cet ensemble d'objets. Pour ce faire, il faut assigner un objet spécifique à chaque constante. Par exemple, on assigne un objet à la constante a, le service Informatique de l'entreprise considérée à la constante informatique, l'employée Marie à la constante marie, etc. L'ensemble d'objets considérés est appelé le domaine de discours ; il est noté D. Chaque fonction à n arguments est interprétée comme une fonction de Dⁿ dans D. Un prédicat représente une relation particulière entre les objets de D, qui peut être vraie ou fausse. Définir cette relation revient à définir les tuples d'objets qui satisfont le prédicat. L'ensemble des tuples satisfaisant le prédicat constitue son extension.

Par exemple, la formule :

peut être interprétée sur l'ensemble des personnes {Pierre, Paul, Marie}, qui constitue alors le domaine de discours. DIRIGE peut être interprété comme la relation binaire « est chef de » ; MEMESERVICE peut être interprété comme la relation binaire « travaille dans le même service ». La formule est vraie si Pierre, Paul et Marie travaillent dans le même service.

Un univers de discours infini peut être retenu pour interpréter la formule ∀x (x < SUCC(x)). En effet, cette formule peut être interprétée sur l'ensemble des entiers positifs {1,2,3…} qui est infini. < est alors la relation « est inférieur à » et SUCC la fonction qui à tout entier associe son successeur. Il est clair que cette formule est vraie sur les entiers.

Ainsi, étant donnée une interprétation d'une formule sur un domaine de discours, il est possible d'associer une valeur de vérité à cette formule. Pour éviter les ambiguïtés (les formules pouvant avoir plusieurs valeurs de vérité), nous considérons seulement les formules dans lesquelles toutes les variables sont quantifiées, appelées formules fermées. Toute formule fermée F a une unique valeur de vérité pour une interprétation donnée sur un domaine de discours D. Cette valeur notée V(F) se calcule ainsi :

V(F1 ∨ F2) = V(F1) ∨ V(F2)
V(F1 ∧ F2) = V(F1) ∧ V(F2)
V(¬ F1) = ¬ V(F1)
V(∀x F) = V(F x=a) ∧ V(F x=b) ∧ … où a, b, … sont les constantes de D.
V(∃x F) = V(F x=a) ∨ V(F x=b) ∨ … où a, b, … sont les constantes de D.
V(P(a,b…)) = Vrai si [a,b…] satisfait la relation P et Faux sinon.

Un modèle d'une formule logique est une interprétation sur un domaine de discours qui rend la formule vraie. Par exemple, les entiers sont un modèle pour la formule ∀x (x < SUCC(x)) avec l'interprétation indiquée ci-dessus. En effet, en appliquant les règles ci-dessus, on calcule :

V(∀x (x < SUCC(x))) = V(1 < 2) ∧ V(2<3) ∧ V(3<4) ∧… = Vrai.

Toute formule fermée, c'est-à-dire à variables quantifiées, peut se simplifier et s'écrire sous une forme canonique sans quantificateurs, appelée forme clausale. La forme clausale nécessite d'écrire la formule comme un ensemble de clauses.

Une clause ayant un seul littéral situé après l'implication (on dit en tête de clause), donc un seul Qi, est dite clause de Horn.

Par exemple :

ENTIER(x) ∧ (x > 0) ⇒ (x < SUCC(x)) ∨ (x > SUCC(x))
DIRIGE(x,y) ∧ MEMESERVICE(x,y) ⇒ AIME(x,y) ∨ DETESTE(x,y)

sont des clauses.

ENTIER(x) ∧ (x > 0) ⇒ (x < SUCC(x))
DIRIGE(x,y) ∧ MEMESERVICE(x,y) ⇒ AIME(x,y)

sont des clauses de Horn.

La transformation d'une formule fermée en clauses s'effectue par des transformations successives que nous décrivons brièvement ci-dessous. Nous illustrons les transformations avec la formule :

∀x ∃y ((DIRIGE(x,y) ∨ DIRIGE(y,x)) ⇒ MEMESERVICE(x,y)).

1. Élimination des implications. Ceci s'effectue simplement en remplaçant toute expression de la forme A ⇒ B par ¬A ∨ B. En effet, ces expressions sont équivalentes du point de vue logique. La formule choisie en exemple devient :

    

   Sélectionnez

   ∀x ∃y (¬ (DIRIGE(x,y) ∨ DIRIGE(y,x)) ∨ MEMESERVICE(x,y)).

2. Réduction de la portée des négations. Le but est de faire que les négations s'appliquent directement à des prédicats atomiques. Pour cela, on utilise de manière répétée les transformations :

    

   Sélectionnez

   ¬ (A ∨ B) devient ¬A ∧ ¬B;
   ¬ (A ∧ B) devient ¬A ∨ ¬B;
   ¬ (∀xA) devient ∃x¬A;
   ¬ (∃xA) devient ∀x¬A;
   ¬ (¬ A) devient A.

   L'exemple devient :

    

   Sélectionnez

   ∀x ∃y ((¬ DIRIGE(x,y) ∧ ¬ DIRIGE(y,x)) ∨ MEMESERVICE(x,y)).

3. Mise en forme prenex. Il s'agit simplement de mettre les quantificateurs avec la variable quantifiée en tête de formule. Cette étape peut nécessiter de renommer les variables afin d'éviter les confusions de quantification. Notre exemple reste ici inchangé.

4. Élimination des quantificateurs. Afin de simplifier encore, les variables quantifiées existentiellement sont remplacées par une constante paramètre dite constante de Skolem. En effet, s'il existe x satisfaisant une formule, il est possible de choisir une constante s désignant cette valeur de x. Attention, si une variable quantifiée par « quel que soit » apparaît avant la variable quantifiée par « il existe », la constante choisie dépend de la première variable. Par exemple, dans le cas ∀x ∃y (pour tout x, il existe y, mais le y dépend de x), on remplacera donc y par s(x), c'est-à-dire une fonction de Skolem qui matérialise la constante y dépendant de x. Ainsi, il est possible d'éliminer les variables quantifiées par « il existe ». Après cette transformation, toute variable restante est quantifiée par « quel que soit ». On peut donc oublier d'écrire les quantificateurs (c'est implicitement ∀). Notre exemple devient alors :

    

   Sélectionnez

   ((¬ DIRIGE(x,s(x)) ∧ ¬ DIRIGE(s(x),x)) ∨ MEMESERVICE(x,s(x))).

5. Mise en forme normale conjonctive. La formule restante est une combinaison par des « ou » et des « et » de littéraux positifs ou négatifs (prédicats atomiques précédés ou non d'une négation). Elle peut être écrite comme une conjonction (∧) de disjonction (∨) en distribuant les « et » par rapport aux « ou » à l'aide de la règle :

    

   Sélectionnez

   A ∨ (B ∧ C) devient (A ∨ B) ∧ (A ∨ C).

   L'exemple devient ainsi :

    

   Sélectionnez

   (¬ DIRIGE(x,s(x)) ∨ MEMESERVICE(x,s(x))) ∧ (¬ DIRIGE(s(x),x)) v MEMESERVICE(x,s(x))).

6. Écriture des clauses. Finalement, il est simple d'écrire chaque clause sur une ligne en remplaçant les « et » par des changements de lignes. De plus, profitant du fait que ¬ A ∨ B s'écrit A ⇒ B, on peut écrire tous les prédicats négatifs d'abord en éliminant la négation et en les connectant par ∧, puis tous les prédicats positifs connectés par ∨. On obtient bien ainsi une suite de clauses, définies comme ci-dessus. Avec l'exemple, on obtient deux clauses (d'ailleurs de Horn) :

DIRIGE(x,s(x)) ⇒ MEMESERVICE(x,s(x))
DIRIGE(s(x),x)) ⇒ MEMESERVICE(x,s(x))).

Une base de données peut être définie comme l'interprétation d'un langage logique du premier ordre L. En pratique, définir l'interprétation consiste à définir les prédicats vrais. Le langage permet d'exprimer les requêtes, comme nous le verrons ci-dessous. Une contrainte d'intégrité peut être vue comme une requête toujours vraie, donc exprimée avec le langage.

En première approche, le langage logique L ne comporte pas de fonctions. Plus particulièrement, L se compose :

1. De prédicats à n arguments, chaque argument correspondant à un type de données élémentaire ;
2. De constantes, une pour chaque valeur possible des types de données élémentaires.

Comme dans toute interprétation d'un langage logique, un prédicat représente une relation particulière entre les objets du domaine de discours, qui peut être vraie ou fausse. Ici, les objets du domaine de discours sont donc les valeurs possibles de la base. Définir cette relation revient à définir les articles ou n-uplets qui satisfont le prédicat. L'ensemble des n-uplets satisfaisant le prédicat constitue son extension. Cette extension peut être assimilée à un fichier dans une base en réseau ou à une table relationnelle, comme nous le verrons plus loin. Pour rester cohérents avec les bases de données relationnelles qui peuvent être perçues comme une implémentation simple des bases de données logiques, nous appellerons l'extension d'un prédicat une table. Chaque colonne correspond à un argument et est aussi appelée attribut dans le contexte relationnel. Comme déjà dit, une base de données logique pourra être complétée par des règles de déduction : nous parlerons alors de base de données déductive (voir chapitre XV de cet ouvrage).

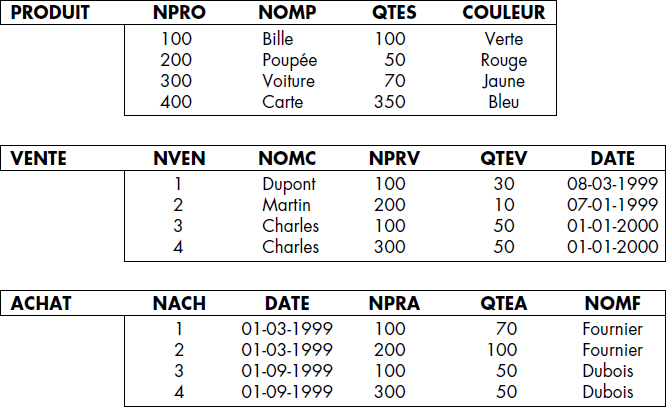
La figure V.1 illustre une base de données logique. En termes de tables, cette base correspond à celles représentées figure V.2. Elle est composée de trois prédicats définis comme suit :

• PRODUIT avec les arguments Numéro de produit (NPRO), nom de produit (NPRO), quantité en stock (QTES), et couleur (COULEUR) ;
• VENTE avec les arguments numéro de vente (NVEN), nom du client (NOMC), numéro du produit vendu (NPRV), quantité vendue (QTEV) et date (DATE) ;
• ACHAT avec les arguments numéro d'achat (NACH), date de l'achat (DATE), numéro du produit acheté (NPRA), quantité achetée (QTEA) et nom du fournisseur (NOMF).

Comme on le voit, seuls les faits positifs, c'est-à-dire ceux satisfaisant l'un des trois prédicats, sont enregistrés dans la base. Ceci constitue l'hypothèse du monde fermé. Les faits non enregistrés dans une extension de prédicat sont supposés faux. Il est vrai que si vous interrogez la base de données que gère votre banque et que vous ne voyez pas de chèque de 100 000 euros crédités ce jour, c'est que le fait que cette somme ait été créditée sur votre compte est faux ! Des chercheurs ont essayé de lever cette hypothèse : on tombe alors dans l'hypothèse du monde ouvert, ou un fait non enregistré peut être inconnu [Reiter78].

PRODUIT (100, BILLE, 100, VERTE)
PRODUIT (200, POUPEE, 50, ROUGE)
PRODUIT (300, VOITURE, 70, JAUNE)
PRODUIT (400, CARTE, 350, BLEU)
VENTE (1, DUPONT, 100, 30, 08-03-1999)
VENTE (2, MARTIN, 200, 10, 07-01-1999)
VENTE (3, CHARLES, 100, 50, 01-01-2000)
VENTE (4, CHARLES, 300, 50, 01-01-2000)
ACHAT (1, 01-03-1999, 100, 70, FOURNIER)
ACHAT (2, 01-03-1999, 200, 100, FOURNIER)
ACHAT (3, 01-09-1999, 100, 50, DUBOIS)

Les questions et les contraintes d'intégrité sur la base peuvent alors être exprimées comme des formules dans le langage logique. Cependant, celui-ci doit être étendu pour inclure les opérateurs de comparaison arithmétique {=, <, ≤, >, ≥, ≠} comme des prédicats particuliers, dont la valeur de vérité est calculée par les opérations usuelles des calculateurs.

La réponse à une question F(x1, …, xn) - où x1, …, xn sont des variables libres dans la formule F - est alors l'ensemble des n-uplets <e1, …, ep> tels que F(e1, …, ep) est vraie. Certaines formules doivent être toujours vraies sur l'interprétation que constitue la base : ce sont alors des contraintes d'intégrité. Cette vue logique des bases de données a donné naissance à deux calculs permettant d'exprimer des questions et des contraintes d'intégrité sur les bases : le calcul de domaine et le calcul de tuple. Dans le premier, les objets de l'interprétation logique sont les valeurs atomiques de données ; dans le second, ce sont les faits composites correspondant aux n-uplets, encore appelés tuples. Nous étudions ces deux calculs ci-dessous.

Le calcul relationnel de domaines [Codd72] se déduit donc de la logique du premier ordre. Les données sont les constantes. Les prédicats utilisés sont :

1. Les prédicats extensionnels contenant les enregistrements de la base ; chaque enregistrement est un tuple typé selon un prédicat extensionnel ; les prédicats étant naires, une variable ou une constante est utilisée comme argument de prédicat ; les variables sont alors implicitement typées selon le type de l'argument pour lequel elles apparaissent ;
2. Les prédicats de comparaison entre une variable et une constante, ou entre deux variables, construits à l'aide des opérateurs {=, ≤, <, ≥, >, ≠}.

Une question en calcul relationnel de domaine s'écrit donc sous la forme suivante :

{x, y… | F(x,y, …)}

F est une formule logique composée à partir de prédicats extensionnels et de comparaison ; les variables résultats x, y, …, sont des variables libres dans F.

La notion suivante résume la définition du calcul de domaine.

La BNF du calcul relationnel de domaine est définie figure V.3. Pour simplifier, les formules sont écrites en forme prenex (quantificateurs devant). En pratique, une simplification d'écriture permet de regrouper des prédicats de restriction du type (x = a) et des prédicats de définition de variable du type P (x, …) en écrivant P (a, …). Toute variable apparaissant dans le résultat doit être définie dans un prédicat extensionnel et doit rester libre dans la formule spécifiant la condition. Une variable non utilisée, ni en résultat, ni dans un critère de comparaison, peut être remplacée par la variable muette positionnelle notée « - ».

<question> : := "{" (<résultat>) "|" <formule> "}"
<résultat> : := <variable> | <variable>, <résultat>
<formule> : := <quantification> <formule libre> | <formule libre>
<quantification> ::= ∀ <variable> | ∃ <variable>
                  | <quantification> <quantification>
<formule libre> : := <formule atomique>
                  | <formule libre> ∧ <formule atomique>
                  | <formule libre> ∨ <formule atomique>
                  | <formule libre> ⇒ <formule libre>
                  | ¬ <formule libre>
                  | (<formule libre>)
<formule atomique> : := <prédicat extensionnel> (<arguments>)
                  | <terme> <comparateur> <terme>
<arguments> : := <terme> | <terme>, <terme>
<terme> : := <variable> | <constante>
<comparateur> : := = | < | ≤ | > | ≥ | ≠

Nous illustrons le calcul de domaine sur la base logique introduite ci-dessus décrivant des achats et des ventes de produits stockés dans un magasin. Le schéma de la base est le suivant :

PRODUIT (NPRO, NOMP, QTES, COULEUR)
VENTE (NVEN, NOMC, NPRV, QTEV, DATE)
ACHAT (NACH, DATE, NPRA, QTEA, NOMF)

Le prédicat extensionnel PRODUIT se compose des attributs numéro de produit (NPRO), nom du produit (NOMP), quantité en stock (QTES) et couleur (COULEUR). Le prédicat VENTE décrit les ventes de produits effectuées et se compose des attributs numéro de vente (NVEN), nom du client (NOMC), numéro du produit vendu (NPRV), quantité vendue (QTEV) et date de la vente (DATE). Le prédicat ACHAT définit les achats effectués aux fournisseurs. Il contient les attributs numéro d'achat (NACH), date d'achat (DATE), numéro du produit acheté (NPRA), quantité achetée (QTEA) et nom du fournisseur (NOMF). Pour simplifier la lecture, nous utilisons des variables rappelant le nom du domaine. Notez que les quantificateurs existentiels dans les formules peuvent être omis, car ils sont implicites si la variable est libre et ne figure pas en résultat.

• (Q1) Donner la liste des noms et des couleurs de tous les produits :

   

  Sélectionnez

  {(p,c) | PRODUIT (-,p,-,c)}

• (Q2) Donner les noms et les quantités en stock des produits de couleur rouge :

   

  Sélectionnez

  {(p,q) | PRODUIT (-, p, q, "Rouge")}

• (Q3) Donner, pour chaque produit en stock, le nom du fournisseur associé :

   

  Sélectionnez

  {(p,f) | ∃n (PRODUIT (n, p, -, -) ∧ ACHAT (-, -, n, -, f))}

• (Q4) Donner, pour chaque produit en stock en quantité supérieure à 100 et de couleur rouge, les triplets nom de fournisseurs ayant vendu ce type de produit, nom de client ayant acheté ce type de produit et nom du produit :

   

  Sélectionnez

  {(f, c, p) | ∃n ∃q (PRODUIT (n, p, q, "Rouge") ∧ ACHAT (-, -, n, -, f)
  ∧ VENTE (-, c, n, -, -) ∧ (q > 100))}

• (Q5) Donner les noms des clients ayant acheté au moins un produit de couleur verte :

   

  Sélectionnez

  {(c) | ∃n (VENTE (-, c, n, -, -) ∧ PRODUIT (n, -, -, "Verte"))}

• (Q6) Donner les noms des clients ayant acheté tous les produits stockés :

   

  Sélectionnez

  {(c) | ∀p (PRODUIT (p, -, -, -) ⇒ VENTE (-, c, p, -, -))}

• (Q7) Donner les noms des produits fournis par tous les fournisseurs et achetés par au moins un client :

{(p) | ∀f (ACHAT(-,-, -, -, f) ⇒ ACHAT (-, -, p, -, f))
∧ ∃c VENTE (-, c, p, -, -)}

Le langage Query-By-Exemple (QBE) [Zloof77] est conçu pour être utilisé à partir d'un terminal. Il a été développé par M. ZLOFF à IBM Yorkton Heights. Il est commercialisé par IBM au-dessus de DB2 depuis 1983 et plus récemment par de nombreux autres constructeurs avec des présentations variées, par exemple par Microsoft dans ACCESS. Ce langage peut être considéré comme une mise en œuvre visuelle (basée sur des tableaux affichés) du calcul relationnel de domaine.

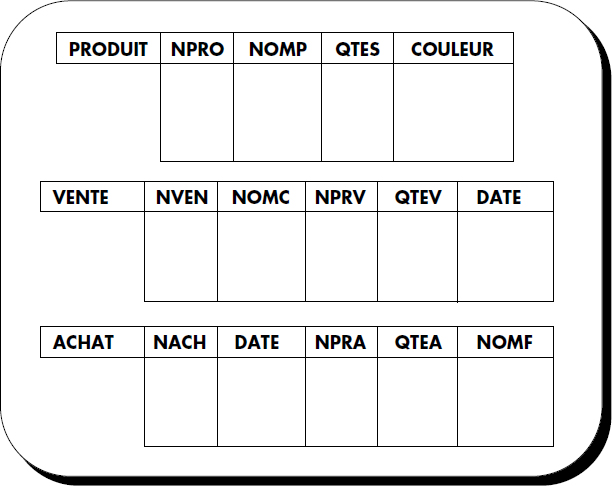
L'idée de base du langage est de faire formuler une question à l'utilisateur à partir d'un exemple d'une réponse possible à la question. Pour cela, l'utilisateur provoque tout d'abord l'affichage du schéma des tables nécessaires à la question qu'il désire poser (sous forme de squelettes de tables) par frappe du nom des tables correspondantes. Ainsi, des tables vides (avec seulement les en-têtes de colonnes et le nom de la relation associée) apparaissent sur l'écran. Elles correspondent bien sûr aux définitions des prédicats extensionnels de la base logique. Par exemple, il est possible d'afficher le schéma des tables PRODUIT, VENTE et ACHAT comme représenté figure V.4.

Comme indiqué ci-dessus, QBE peut être vu comme une implantation à deux dimensions du calcul relationnel de domaines. Pour cela, les règles suivantes sont utilisées :

1. Les résultats (attributs à projeter en relationnel) sont définis en frappant « P. » (PRINT) dans la colonne associée. Il est possible d'imprimer tous les attributs d'une table en frappant « P. » dans la colonne contenant le nom de la table.
2. Les constantes sont tapées directement dans la colonne de l'attribut associé, précédées de l'opérateur de comparaison les reliant à l'attribut si ce n'est pas = (c'est-à-dire <, ≤, >, ≥, ≠). Dans le cas où un critère complexe est nécessaire avec des conjonctions (and) et disjonctions (or), il est possible d'ouvrir une boîte condition et de taper le critère dans cette boîte (par exemple A < 10 AND A > 5).
3. Les variables domaines sont désignées par des valeurs exemples soulignées tapées dans la colonne les spécifiant ; la valeur exemple soulignée est en fait le nom de la variable domaine ; par suite, QBE associe deux valeurs soulignées identiques comme définissant une même variable.
4. Le quantificateur « quel que soit » est appliqué à une variable en tapant « ALL. » devant son nom (l'exemple souligné) alors que toute variable non imprimée non précédée de P. est implicitement quantifiée par « il-existe ».
5. Le connecteur ou (or) est exprimé en utilisant deux lignes (deux exemples) comme si l'on avait en fait deux questions, l'une avec la partie gauche et l'autre avec la partie droite de la qualification (après mise en forme normale disjonctive).

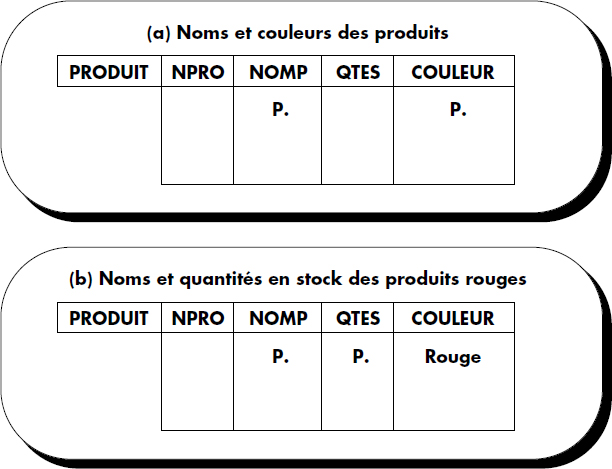
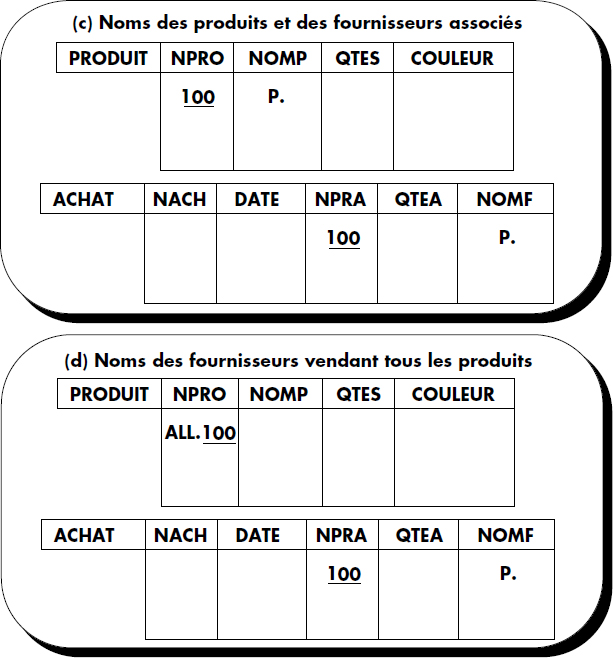
À l'aide de ces règles simples, il est possible d'exprimer toute question du calcul relationnel de domaines. Nous avons formulé (voir figure V.5) les questions introduites ci-dessus (Q1 à Q7) sur la base des produits. Remarquez l'aspect naturel de ce langage par l'exemple qui peut être simplement paraphrasé.

QBE offre quelques possibilités supplémentaires par rapport au calcul de domaines. En particulier, il est possible d'enlever l'élimination automatique des doubles lors des projections finales en spécifiant le mot clé ALL devant une variable résultat à imprimer. Par exemple, l'édition de tous les noms des clients à qui l'on a vendu des produits (sans élimination des doubles) sera effectuée en réponse à la question représentée figure V.6.

Il est également possible d'obtenir des résultats triés par ordre croissant (mot clé AO.) ou décroissant (mot clé DO.). Par exemple, l'édition des noms de produits en stock en quantité supérieure à 100 par ordre alphabétique descendant sera obtenue par exécution de la question représentée figure V.7.

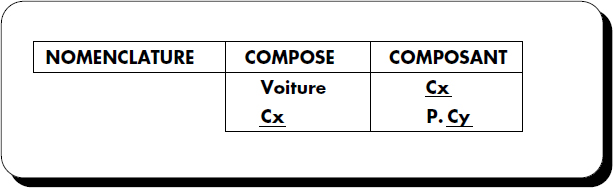
De plus, QBE offre des facilités pour accomplir les opérations de type fermeture transitive de graphe. Le calcul de la fermeture transitive est impossible avec les langages basés sur le calcul de prédicats. Soit par exemple la relation représentée figure V.8. Tout composant peut aussi être un composé. Si l'on veut rechercher les composants de voiture au deuxième niveau, il est possible avec QBE d'utiliser la question représentée figure V.9.

Pour rechercher les composants de niveau n à partir d'un composant (ou les composés de niveau n à partir d'un composé), il faut une question à n lignes. Ceci peut être fastidieux. Afin de simplifier, QBE autorise le mot clé L entre parenthèses précédé d'un nombre de niveaux (par exemple (2L)). Ainsi, la question précédente pourra aussi être formulée comme sur la figure V.10.

La fermeture transitive du composé VOITURE consiste à rechercher les composants de tout niveau. Ceci est effectué en fixant un niveau variable, comme représenté figure V.11. Une telle question n'est pas exprimable à l'aide du calcul relationnel de domaines, mais nécessite la récursion que nous étudierons dans le cadre des BD déductives. Il est aussi possible d'obtenir les composants de dernier niveau à l'aide du mot clé LAST.

Finalement, QBE dispose également des fonctions d'agrégats qui dépassent la logique du premier ordre. Les fonctions CNT (décompte), SUM (somme), AVG (moyenne), MAX (maximum) et MIN (minimum) permettent de faire des calculs sur plusieurs valeurs de variables, celles-ci étant sélectionnées par des critères exprimés par une question. Ces fonctions peuvent être appliquées à toute variable résultat à condition qu'elle soit précédée de ALL. Si l'on désire éliminer les doubles avant application de la fonction, il faut appliquer préalablement l'opérateur unique (mot clé UNQ). Par exemple, si l'on veut connaître la quantité en stock des produits de nom « Vins », on écrira la question représentée figure V.12.

QBE permet aussi la mise à jour des prédicats extensionnels, c'est-à-dire des tables. Il est possible :

• d'insérer des n-uplets dans une relation (opérateur I. en première colonne) ; la figure V.13 illustre l'insertion du produit de clé 200 ;
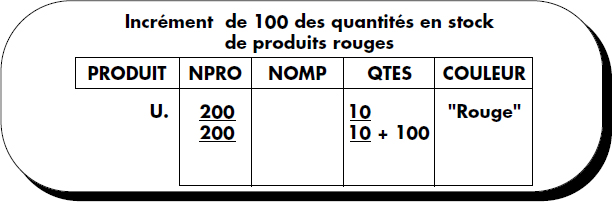
• de modifier des attributs de n-uplet (opérateur U. en première colonne) ; la figure V.14 illustre la mise à jour des quantités en stock pour les produits de couleur rouge ;
• de supprimer les n-uplets dans une relation obéissant à un critère de sélection donné (opérateur « D. » en première colonne) ; la figure V.15 illustre la suppression des produits rouges de la relation produit.

QBE permet enfin une définition très dynamique de la base de données. Il est possible de créer et détruire des prédicats extensionnels (tables). De plus, il est permis d'étendre un prédicat en ajoutant des attributs. QBE est donc un langage très souple et complet, issu de la logique du premier ordre appliquée aux tables relationnelles.

Les seuls termes considérés sont les constantes associées aux n-uplets composant les faits et les fonctions génératrices des attributs notées par le nom de l'attribut appliqué à une variable par la notation pointée (par exemple X.COULEUR). Les prédicats utilisés sont ceux correspondant aux relations extensionnelles ainsi que les prédicats de comparaison {=, <, ≤, ≥, >, ≠}. Les prédicats extensionnels permettent la définition de la portée d'une variable sur une table R par une formule atomique du type R (X), X étant donc une variable tuple et R une table.

L'élément essentiel différenciant le calcul de tuples par rapport aux calculs de domaines est bien sûr l'association aux variables de tuples des extensions de prédicats et non plus de valeurs de domaines, comme avec le calcul de domaine. Cela change légèrement la syntaxe du calcul. Nous définissons plus précisément le calcul de tuples ci-dessous. La syntaxe du calcul est définie en BNF figure V.16.

<question> : := "{" (<résultat>) "|" <formule> "}"
<résultat> : := <variable>.<attribut> | <résultat>, <résultat>
<formule> : := <quantification> <formule libre> | <formule libre>
<quantification> ::= ∀ <variable> | ∃ <variable>
                  | <quantification> <quantification>
<formule libre> : := <formule atomique>
                  | <formule libre> ∧ <formule atomique>
                  | <formule libre> ∨ <formule atomique>
                  | <formule libre> ⇒ <formule libre>
                  | ¬ <formule libre>
                  | (<formule libre>)
<formule atomique> : := <predicat extensionnel> (<variable>)
                  | <terme> <comparateur> <terme>
<terme> : := <variable>.<attribut> | <constante>
<comparateur> : := = | < | ≤ | > | ≥ | ≠

Nous exprimons maintenant en calcul relationnel de tuples les questions exprimées ci-dessus en calcul de domaines sur la base des produits.

• (Q1) Donner la liste des noms et des couleurs de tous les produits :

   

  Sélectionnez

  {(P.NOMP, P.COULEUR) | PRODUIT(P)}

• (Q2) Donner les noms et les quantités en stock des produits de couleur rouge :

   

  Sélectionnez

  {(P.NOMP, P.QTES) | PRODUIT(P) ∧ P.COULEUR = "ROUGE"}

• (Q3) Donner pour chaque produit en stock, le nom du fournisseur associé :

   

  Sélectionnez

  {(P.NOMP, A.NOMF) | PRODUIT(P) ∧ ACHAT(A) ∧ P.NPRO=A.NPRA}

• (Q4) Donner, pour chaque produit en stock en quantité supérieure à 100 et de couleur rouge, les couples nom de fournisseurs ayant vendu ce type de produit et nom de client ayant acheté ce type de produit, avec le nom du produit :

   

  Sélectionnez

  {(P.NOMP, A.NOMF, V.NOMC) | PRODUIT(P) ∧ ACHAT(A) ∧ VENTE(V)
  ∧ P.QTES > 100 ∧ P.COULEUR = "Rouge" ∧ P.NPRO = V.NPRV
  ∧ P.NPRO = A.NPRA}

• (Q5) Donner les noms des clients ayant acheté au moins un produit de couleur verte :

   

  Sélectionnez

  {(V.NOMC) | VENTE (V) ∧ ∃P (PRODUIT (P) ∧ V.NPRV = P.NPRO
  ∧ P.COULEUR = "Verte")}

• (Q6) Donner les noms des clients ayant acheté tous les produits stockés :

   

  Sélectionnez

  {(V1.NOMC) | VENTE (V1) ∧ ∀P (PRODUIT (P) ⇒ (∃V2 (VENTE(V2)
  ∧ V2.NPRV = P.NPRO ∧ V2.NOMC = V1.NOMC)))}

• (Q7) Donner les noms des produits fournis par tous les fournisseurs et achetés par au moins à un client :

{(P.NOMP) | PRODUIT(P) ∧ (∀A1 (ACHAT(A1) ⇒ (∃A2 (ACHAT(A2)
∧ A2.NOMF = A1.NOMF ∧ A2.NPRA = P.NPRO)))
∧ (∃V (VENTE(V) ∧ V.NPRV = P.NPRO))}

Les questions (Q6) et (Q7) démontrent la difficulté d'utilisation des quantificateurs « quel que soit » et « il existe ». En général, toute variable apparaissant dans la réponse doit être libre dans la condition. Les « il existe » ne sont utiles qu'à l'intérieur des quantifications universelles.

Un algorithme de déduction est une procédure pour prouver une formule T à partir d'un ensemble de formules {A1, A2…An} connues comme vraies. T est le théorème à démontrer. A1, A2…An sont les axiomes. L'existence d'une preuve de T à partir de A1, A2…An est formellement notée {A1,A2… An} |== T.

Par exemple, à partir des axiomes :

DIRIGE(pierre, marie)
DIRIGE(marie, julie)
∀x ∀y ∀z (DIRIGE(x,y) ∧ DIRIGE(y,z) ⇒ DIRIGE(x,z))

on aimerait déduire le théorème :

DIRIGE(pierre, julie).

Pour prouver un théorème, un algorithme de déduction dérive à partir des axiomes une séquence de formules dont le théorème est la dernière en utilisant des règles d'inférence. Une règle d'inférence est une règle permettant de générer une formule à partir de deux ou plus. Une règle d'inférence correcte permet de générer une formule valide (vraie sur les univers de discours considérés) à partir de formules valides.

Deux règles d'inférences bien connues sont :

• Le modus ponens. Il permet de générer P à partir des deux formules F et F ⇒ P. Intuitivement, cela signifie que si F et F implique P sont prouvées, alors P est prouvée. On écrit formellement :
  
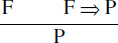
• La spécialisation. Elle permet de générer F(a) à partir de la formule ∀xF(x). Intuitivement, cela signifie que si F(x) est prouvée pour toute valeur de x, alors F(a) est prouvée. On écrit formellement :
  

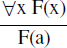
Il existe une règle d'inférence générale pour les formules du premier ordre en forme clausale. Cette règle génère par application récursive toutes les formules qui peuvent être déduites à partir de deux axiomes sous forme de clauses. Il s'agit de la règle d'inférence de Robinson [Robinson65]. Elle s'appuie sur l'algorithme d'unification qui permet de comparer deux formules atomiques.

La capacité à décider si deux formules atomiques peuvent être identifiées par substitution de paramètres est centrale à la plupart des méthodes de déduction. Une unification de deux formules atomiques consiste à les rendre identiques par remplacement de variables dans une formule par des termes de l'autre.

Deux formules atomiques L1(t1,t2…tn) et L2(s1,s2…sn) ne sont pas toujours unifiables. Un algorithme d'unification décide si les deux formules peuvent être identifiées par une substitution de variable valide (renommage ou assignation de valeur). Un tel algorithme (voir figure V.17) retourne :

• SUCCES et une substitution de variable minimale si les deux formules peuvent être identifiées en appliquant la substitution ;
• ECHEC s'il est impossible de les rendre identiques par une substitution de terme unique à chaque variable.

L'algorithme est récursif : il exploite les termes à partir du début en unifiant tête et queue successivement. Il existe beaucoup d'algorithmes d'unification, celui-là n'est qu'indicatif.

Quelques exemples simples permettent d'illustrer l'algorithme. On note {x/t1; y/t2; …} la substitution qui remplace x par t1, y par t2, etc. Les formules DIRIGE(pierre,marie) et DIRIGE(x,y) sont simplement unifiables par la substitution {x/pierre; y/marie}. Les formules DIRIGE(chef(x),pierre) et DIRIGE(chef(chef(pierre)),y) sont unifiables par la substitution {x/chef(pierre); y/pierre}. Les formules DIRIGE(chef(x),x) et DIRIGE(chef(chef(x)),x) ne sont pas unifiables : il faudrait que x devienne à la fois chef(x) et x, ce qui est syntaxiquement impossible.

La méthode de résolution est très simplement basée sur la règle d'inférence de Robinson. Cette règle s'énonce comme suit. Soient C1 et C2 deux clauses de la forme :

C1 = F1 ∨ L1
C2 = L2 ⇒ F2.

De plus, moyennant une substitution s, L1 et L2 sont unifiables (on note L1[s] = L2[s]). La règle de Robinson permet d'inférer la clause F1[s] ∨ F2[s] ; cette nouvelle clause obtenue par disjonction de F1 et F2 et application de la substitution s est appelée résolvant de C1 et C2. Formellement, la règle de Robinson s'écrit :

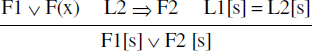
En remarquant que L2 ⇒ F2 peut aussi s'écrire ¬ L2 ∨ F2, puis en remplaçant le « ou » par + et la négation par -, on obtient :

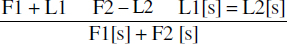
On voit alors que la règle de Robinson permet finalement de réaliser l'addition de clauses avec suppression des parties s'annulant moyennant une substitution s. Il s'agit de la règle de base du calcul symbolique. Elle a une propriété remarquable de complétude : toute formule pouvant être démontrée à partir d'un ensemble d'axiomes se déduit par applications successives de la règle de Robinson aux axiomes et aux résolvants obtenus.

À partir de cette règle d'inférence est construite la méthode de résolution. Cette méthode permet de prouver un théorème à partir d'axiomes non contradictoires. C'est une méthode par l'absurde qui consiste à partir des axiomes et de la négation du théorème et à prouver qu'il y a contradiction. Donc, sous l'hypothèse de non-contradiction des axiomes, c'est que le théorème est valide (car son contraire contredit les axiomes).

En résumé, la méthode procède comme suit :

1. Mettre les axiomes et la négation du théorème (¬T) sous forme de clauses.
2. Ajouter récursivement les résolvants que l'on peut obtenir en appliquant la règle d'inférence de Robinson à l'ensemble des clauses jusqu'à obtention de la clause vide.

La clause vide (tout s'est annulé) ne peut jamais être satisfaite (son modèle est vide) ; par suite, c'est que les axiomes contredisent la négation du théorème. Donc celui-ci est démontré. Il a été démontré que si une preuve du théorème existe, la méthode de résolution se termine et la trouve. Si aucune preuve n'existe, la méthode peut se perdre dans des univers infinis et boucler (de plus en plus de clauses sont générées). La logique du premier ordre est semi-décidable. Pour un approfondissement de cette méthode, consultez [Manna85].

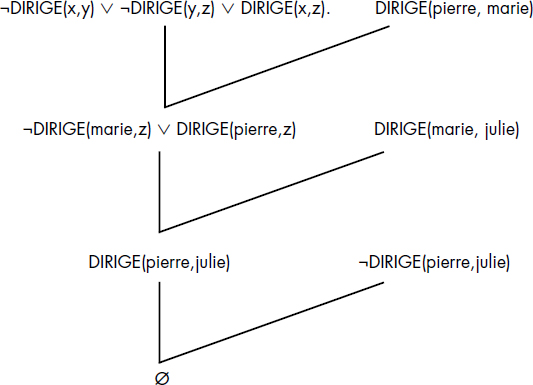
Nous nous contenterons d'illustrer la méthode par un arbre de preuve (figure V.18). Soit à prouver le théorème DIRIGE(pierre, julie) à partir des axiomes non contradictoires :

(A1) DIRIGE(pierre, marie),
(A2) DIRIGE(marie, julie),
(A3) ∀x ∀y ∀z (DIRIGE(x,y) ∧ DIRIGE(y,z) ⇒ DIRIGE(x,z)).

La négation du théorème est ¬ DIRIGE(pierre,julie). Les deux premiers sont des clauses. Le troisième se met simplement sous la forme de la clause :

(A'3) DIRIGE(x,y) ∧ DIRIGE(y,z) ⇒ DIRIGE(x,z)

qui s'écrit encore :

(A''3) ¬DIRIGE(x,y) ∨ ¬DIRIGE(y,z) ∨ DIRIGE(x,z).

L'arbre de preuve (encore appelé arbre de réfutation) représenté figure V.18 montre des unifications et additions successives de clauses qui conduisent à la clause vide. Il permet donc par applications successives de la règle d'inférence de Robinson (chaque nœud R non initial dérive de deux nœuds précédents N1 et N2) de tirer le résolvant vide et ainsi de démontrer que Pierre dirige Julie.